Précédent Suivant Index

2   Les bases du langage de la méthode B

La méthode B permet de formaliser des spécifications et des programmes. Pour cela, elle utilise son propre langage formel. Au niveau des spécifications, il s'agit d'un langage logique reposant sur une version simplifiée ad-hoc de la théorie des ensembles. Ce choix est un peu arbitraire mais peut se justifier par les arguments suivants :

Nous n'allons pas décrire ici en détail tout le langage de la méthode B, nous nous contenterons de détailler un petit nombre de concepts qui nous seront utiles par la suite. Une description plus détaillée est donnée dans l'annexe A de ce document. Nous donnons pour chaque notion à la fois la notation mathématique et une notation ASCII utilisée dans les outils.

2.1   Les expressions

2.1.1   Expressions de base

Parmi les expressions, nous trouvons les constantes entières ainsi que les variables. Nous trouvons également les expressions formées par application des opérateurs arithmétiques usuels (+,-,×,/,mod,...).

Exemple
3 × (n + 3) / k

Remarque
Dans les outils, une variable est formée d'au moins deux caractères, l'expression précédente s'écrira en fait : 3 * (nn + 3) / kk

2.1.2   Combiner deux expressions

Il est souvent utile de composer deux éléments ensemble pour former une paire ordonnée. La paire formée des expressions e1 et e2 est notée e1,e2 ou bien e1 |® e2. Cette seconde notation sera utilisée le plus souvent lorsque la paire représente un élément d'une fonction.
Exemple
x |® x+2 représente la paire (x,x+2) et l'ensemble des paires x |® x+2 pour tous les x entiers représente la fonction qui à x associe x+2.

2.1.3   Les ensembles

Le langage de B permet également de manipuler des ensembles.

Ensembles de base
Ø {} L'ensemble vide
N NAT L'ensemble des entiers naturels
Z INTEGER L'ensemble des entiers relatifs
INT INT L'ensemble des entiers relatifs compris entre MININT et MAXINT
{e} {e} L'ensemble réduit à un élément e
{e1,...,en} {e1,...,en} L'ensemble composé des éléments e1,...,en
Exemple
{1,2,3} est un ensemble. {Ø} est un ensemble composé d'un élément.

Compréhension
Soit P une formule, on peut définir un ensemble par compréhension comme l'ensemble de tous les objets qui vérifient la formule P. On note cet ensemble {z  |  P }.

2.1.4   Autres constructions

Quelques autres constructions primitives nous seront utiles.

n1..n2 (n1..n2) L'ensemble des entiers compris entre n1 et n2 (inclus) avec n1 et n2 des expressions représentants des entiers positifs.
card(E) card(E) Le cardinal (nombre d'éléments) d'un ensemble E fini.

2.2   Les formules

2.2.1   Formules de base

On peut utiliser dans B tous les connecteurs logiques de base à savoir ceux du calcul des prédicats du premier ordre avec égalité. Le tableau suivant introduit les formules atomiques : e1 et e2 représentent des expressions quelconques (entiers, ensembles, paires ...), n1 et n2 sont des expressions qui représentent des entiers.
math & ASCII
e1=e2
n1 > n2
n1 < n2
      
math ASCII
e1¹e2 e1 /= e2
n1 ³ n2 n1 >= n2
n1 £ n2 n1 =< n2

2.2.2   Formules ensemblistes

Une formule atomique particulière importante est la formule qui dit qu'une expression appartient à un ensemble. Nous avons également des notations pour indiquer les relations d'inclusion ou de non inclusion. Dans le tableau suivant, e représente une expression tandis que E, E1 et E2 représentent des ensembles.

math ASCII  
e Î E e:E L'expression e est un objet de l'ensemble E
e ÏE e/:E L'expression e n'est pas un objet de l'ensemble E.
E1 Í E2 E1 <: E2 E1 est un sous-ensemble de E2.
¬ E1 Í E2 E1 /<: E2 E1 n'est pas un sous-ensemble de E2.

2.2.3   Formules composées

Le tableau suivant introduit les formules composées : F, F1 et F2 représentent des formules.
math ASCII
¬ F not(F) négation
F1 Ù F2 F1  &  F2 conjonction
F1 Ú F2 F1  or  F2 disjonction
F1 Þ F2 F1  =>  F2 implication
F1 Û F2 F1  <=>  F2 équivalence
$  var .  F #  var .  F quantification existentielle
"  var .  F !  var .  F quantification universelle
Quantification multiple
Une particularité de B est que la quantification peut avoir lieu simultanément sur plusieurs variables, elles sont alors entourées de parenthèses et séparées par des virgules. Ainsi, on peut écrire la formule suivante :
" (x,y) . (x=y Þ y =x)
qui est équivalente à " x . " y . (x=y Þ y=x)

2.2.4   Les formules bien typées

Dans le langage B, les ensembles servent à contraindre les données; en ce sens ils jouent le rôle des sortes ou des types d'autres langages. Cependant, il est en général indécidable de savoir si un objet e appartient à un ensemble E. En effet vérifier que e Î {z|P(z)} est équivalent à vérifier que P(e) est vrai, or la formule P est arbitraire. Cependant, le langage B propose un système rudimentaire de typage qui permet de distinguer les entiers, les paires, les ensembles ...

N est un type, les machines pourront également être paramétrés par des variables représentant des ensembles arbitraires. Ces variables sont également des types. Si T1 et T2 sont des types, il en est de même du produit cartésien de T1 et de T2, noté T1 × T2 qui est le type des paires (t1,t2) d'éléments t1 de type T1 et t2 de type T2. Si T est un type, il en est de même du type des sous-ensembles de T noté P(T). Ainsi si eiÎ T pour i=1..n, alors {e1,...,en} Î P(T).

Le langage de B impose que les formules écrites soient bien "typées". Cela permet d'empêcher a priori de construire des expressions qui ne représentent effectivement pas des ensembles comme {x| x Ïx}. Pour cela on impose que chaque variable introduite soit contrainte à vivre dans un certain ensemble et que ces ensembles s'organisent de manière cohérente.

Les quantifications universelles, existentielles ainsi que les constructions d'ensemble par compréhension auront donc toujours la forme suivante :
"  var  .  P Þ Q       $  var  .  P Ù Q      {var  |  P Ù Q}
avec P une formule qui contraint chacune des variables z de var. Par exemple z=e, z Î E, z Í E ou z Ì E avec z qui n'apparaît ni dans e ni dans E.

Il faut vérifier que les opérations ensemblistes apparaissant dans la formule sont compatibles avec la hiérarchie. Par exemple si on a x=y alors les types de x et de y doivent être égaux. Dans la relation xÎ X on doit vérifier que X est de type P(U) pour un certain type U et que x est de type U. Si on a X Í Y, on doit vérifier que X et Y sont de type P(U) pour un certain type U.

Exemple
Nous illustrons la procédure de vérification sur un exemple. On suppose qu'un ensemble E arbitraire est donné. Soit la formule :
" (a,b). (a,b) Î P(E) × P(E) Þ {x | x Î E Ù x Î a Ù x Î b } Í E
Comme E est un ensemble paramétrique, les types sont de la forme P(E), E × E, E × P(E),...

On a a de type P(E), b de type P(E), x de type E on vérifie que xÎ a et xÎ b sont des formules bien typées et {x | x Î E Ù x Î a Ù x Î b } est de type P(E), de même E est de type P(E), donc l'inclusion est bien formée.

2.3   Substitution élémentaire

Une notion importante du langage de B est l'opération d'une substitution S sur une formule P qui est notée [S]P.

Une substitution élémentaire est de la forme var:=E. Dans ce cas [var:=E]P représente juste le résultat de la substitution des occurrences libres de var dans P par E.

Exemple
[n:=3]n>m est égal à 3>m.

2.3.1   Variables liées et substitution

Les quantificateurs ont la propriété de lier les variables qu'ils introduisent, c'est-à-dire que le nom de la variable n'intervient plus dans le sens de la formule, seuls les emplacements (on parle d'occurrences) où la variable apparaît dans la formule sont importants.

Ainsi n = 4 et m=4 sont des formules différentes mais $ n.n=4 et $ m.m=4 représentent la même formule.

La variable z est liée dans les formules " z.Q et $ z.Q ainsi que dans l'expression {z| Q}.

Un même nom de variable peut avoir simultanément des occurrences libres et des occurrences liées dans une formule :
n>0 Þ " n.n ³ 0

Lors de la substitution [var:=E]P, il faut être attentif à ne remplacer que les occurrences libres de var dans P et de plus, il ne faut pas que les variables libres de E se retrouvent liées par des quantificateurs de P

Exemple
Soit la formule P définie comme étant n>0 Þ " n.$ m. m ³ n On souhaite calculer [n:=m+1]P. Une opération naïve de remplacement donnerait le résultat erroné :
m+1>0 Þ " n.$ m. m ³ m+1
En renommant les variables liées de P on obtient une formulation équivalente de P:
n>0 Þ " n0.$ m0. m0 ³ n0
Il est alors licite de calculer la substitution comme un simple remplacement et on obtient le résultat correct suivant :
m+1>0 Þ " n0.$ m0. m0 ³ n0

Principe de la substitution
Pour calculer le résultat d'une substitution [var:=E]P on renomme les variables liées de P de manière à ce qu'elles soient différentes des variables libres de P et de E puis on procède à un remplacement de var par E dans la formule ainsi obtenue.

2.3.2   Substitutions multiples

Il est possible de substituer de manière simultanée plusieurs variables dans une formule. On notera cette opération
[x1,...,xn:=e1,...,en]P
Toutes les variables xi doivent être distinctes. Une substitution multiple peut alternativement être notée :
x1 :=e1 || ... || xn:=en

Remarque
La substitution est simultanée, en particulier [x,y:=a,b]P n'est pas équivalent à [x:=a][y:=b]P. L'exemple suivant illustre ce phénomène :
[x,y:=y,x]x=y º y=x        [x:=y][y:=x]x=y º [x:=y]x=x º y=y

2.3.3   Substitutions généralisées

Le langage B permet de décrire des substitutions généralisées qui serviront à représenter des programmes. Celles-ci sont décrites dans la section 3.

2.4   Les relations et fonctions

En théorie des ensembles, les relations sont un cas particulier d'ensemble (des ensembles de paires) et les fonctions sont un cas particulier de relations. Cependant ces concepts essentiels bénéficient de notations spécifiques que nous décrivons ici.

2.4.1   Relations

Dans le tableau suivant, E, E1 et E2 représentent des ensembles tandis que R, R1 et R2 représentent des relations.
E1 « E2 E1 <-> E2 L'ensemble des relations entre éléments de E1 et de E2
    P(E1× E2)
R1;R2 R1 ; R2 Composition des relations R1 et R2
    (x,y) Î (R1;R2) Û $ z. ((x,z) Î R1 Ù (z,y) Î R2)
id(E) id(E) la relation identité sur l'ensemble E
R-1 R~ relation inverse de R
    (x,y) Î R-1 Û (y,x) Î R
E <| R E <| R la restriction de la relation R au domaine E
    (x,y) Î (E <| R) Û (x Î E Ù (x,y) Î R)
R |> E R |> E la restriction de la relation R à l'image E
    (x,y) Î (R |> E) Û ((x,y) Î RÙ y Î E )

Ensembles définis à partir de relations
(A.4.1)
dom(R) dom(R) le domaine de la relation R
    x Î dom(R) Û ($ y. (x,y)Î R)
ran(R) ran(R) l'image de la relation R
    y Î ran(R) Û ($ x. (x,y)Î R)

2.4.2   Fonctions

Les fonctions du système B sont, comme en mathématique, des cas particuliers de relations. Une fonction de E1 dans E2 est une relation binaire sur E1 × E2, c'est-à-dire un ensemble de couples (x,y) aussi notés x|® y. Une relation R est dite fonctionnelle si lorsque x |® y1 Î R et x |® y2 Î R alors y1=y2. Une fonction f de E1 dans E2 est une relation fonctionnelle. L'ensemble des relations fonctionnelles de E1 dans E2 est noté E1 +-> E2. Le domaine d'une fonction f est l'ensemble dom(f) des x pour lesquels il existe y tel que x |® y Î f. Si x est dans le domaine de f alors on note f(x) l'unique y tel que x |® y Î f.

Une fonction est totale si son domaine est égal à l'ensemble E1 tout entier.

D'autres notions sur les fonctions sont définies en A.4.2.

2.4.3   Séquences

Les séquences sont des suites ordonnées d'objets d'un ensemble E. Une manière de les modéliser mathématiquement est de les voir comme des fonctions de N dans E dont le domaine est soit l'ensemble vide (dans le cas de la séquence vide) soit l'ensemble 1..n pour n un entier strictement positif. L'ensemble des séquences sur E est noté seq(E), les principales constructions sur les séquences sont rappelées en annexe (A.4.3).

Finalement, nous pouvons introduire des constantes correspondant à des chaînes de caractères écrites entre guillemets comme "Hello".

2.4.4   Exemple

Les notions que nous avons introduites sont suffisantes pour modéliser un petit problème.

On s'intéresse à un ensemble de personnes et leurs liens de parenté et de mariage. On suppose donné un ensemble personnes représentant les personnes. On cherche à modéliser de manière ensembliste les notions de femmes, hommes, les relations de a_pour_epoux, a_pour_épouse, a_pour_mère, a_pour_père, a_pour_frère, a_pour_enfant, est_marié_à sachant que les principes suivants doivent être respectés :
  1. chaque personne est soit un homme soit une femme,
  2. nulle personne n'est à la fois homme et femme,
  3. seules les femmes ont des époux qui sont des hommes,
  4. chaque femme a au plus un mari qui n'est le mari d'aucune autre femme,
  5. une mère est une femme mariée,
  6. le père est l'époux de la mère.
On identifie les données minimales qui doivent être primitives (par exemple l'ensemble hommes, les relations a_pour_epoux et a_pour_mère). Les contraintes imposent des restrictions sur la nature de ces objets. On peut ensuite définir les autres notions en fonction des notions primitives. Le système B privilégie l'utilisation de symboles algébriques pour représenter les contraintes sur les données sans introduire de quantificateur. Cela permet d'automatiser plus simplement les preuves.

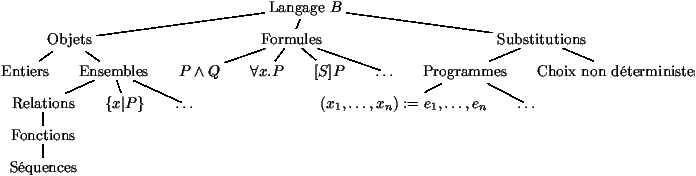
Ce qu'il faut retenir
Le langage associé à la méthode B permet de manipuler différentes classes d'objet :



2.5   Méthodes de preuve

2.5.1   Raisonner sur les objets

Nous n'avons donné aucun système d'axiomes pour raisonner sur les objets introduits. Un tel système peut se trouver dans le livre "The B-Book" de J.-R. Abrial. Cependant une présentation effectuée de manière rigoureuse est très fastidieuse. Pour ce cours, il est suffisant de raisonner de manière semi-formelle, comme on peut le faire en mathématiques.

2.5.2   Raisonner sur les programmes

Dès lors qu'on connaît ce qui est attendu d'un programme (sa spécification) et qu'on connaît la manière dont le programme va s'exécuter (sa sémantique), il est possible de faire une preuve de correction du programme.

2.5.3   Logique de Hoare

Hoare dès les années 70, puis Floyd et Dijkstra ont développé l'idée qu'il fallait prouver les programmes. Pour pouvoir raisonner sur un programme, il faut savoir les représenter et se donner des règles et méthodes de preuve sur ces objets.

Modélisation du programme
L'exécution d'un programme transforme l'état de la mémoire de la machine. La partie qui nous intéresse correspond aux valeurs associées aux variables du programme. On représente souvent l'environnement d'exécution du programme comme une fonction qui à chaque variable du programme associe une valeur (entier, chaîne de caractères, ensemble fini,...)

Il n'est pas raisonnable de raisonner globalement sur le programme comme une transformation de l'état de la mémoire. Hoare a donc proposé ce qui est connu comme la sémantique axiomatique ou la logique de Hoare. L'idée principale de la logique de Hoare, est de ne pas raisonner sur la mémoire globalement mais seulement sur les valeurs des variables apparaissant dans le programme.

Si en un point du programme, je démontre qu'une propriété P(x) est vérifiée, cela signifie que la propriété P(v) est vraie, avec v la valeur associée à la variable x dans la mémoire à ce point d'exécution du programme.

Exemple
Que fait le programme suivant ? Comment le démontrer ?

n:=5;
i:=n; res:=1;
while i > 0 do res:=i*res; i:=i-1 end
print(res)

La logique de Hoare établit un système de déduction qui permet de démontrer des triplets de Hoare
{f}P{y}
dans lesquels P est un programme et f et y sont des formules portant sur les variables du programme. Lorsqu'un triplet {f}P{y} est vrai cela signifie que si les valeurs des variables de P satisfont la formule {f} alors après l'exécution de P, les nouvelles valeurs de ces variables satisferont la propriété y.

Exemple-suite
On peut annoter le programme précédent par des assertions
n:=5;
{n³ 0} i:=n; res:=1;
{res*i!=n!}
while i > 0 do res:=i*res; i:=i-1 end
{i=0 Ù res=n!*i!}
print(res) {res=n!}

Un programme vu comme un transformateur de prédicat
La logique de Hoare permet de voir les programmes non plus comme des fonctions qui transforment les états de la mémoire mais comme des transformateurs de prédicats. Si on se donne un programme P et une propriété y portant sur les variables de P alors on peut définir en fonction de P la plus faible condition f pour que {f}P{y} soit vérifié. On note wp(P,y) la propriété f ainsi définie.

Elle doit vérifier les deux conditions suivantes :
{wp(P,y)}P{y}      " f.{f}P{y} Þ (f Þ wp(P,y))

Les règles de la logique de Hoare permettent de calculer effectivement wp(P,y) pour un y quelconque en fonction de P, lorsque P ne contient pas de boucle. Par exemple :

wp(x:=e,y)=y[x¬ e]
wp(if C then P else Q end,y) = (C Þ wp(P,y)) Ù (¬ C Þ wp(Q,y))
wp(P1;P2,y) = wp(P1,wp(P2,y))
Le cas des boucles
L'introduction de boucles dans les programmes complique le raisonnement. Il est nécessaire de produire un invariant qui est une propriété qui sera vérifiée à l'entrée dans la boucle et préservée par le corps de la boucle. D'autre part, une boucle peut ne pas terminer. On distingue alors deux variantes de la logique de Hoare que l'on qualifie de partielle et totale.
Des exemples de logique de Hoare seront développés en exercice (1).

Précédent Suivant Index