


2 Les bases du langage de la méthode B
La méthode B permet de formaliser des spécifications et des
programmes. Pour cela, elle utilise son propre langage formel. Au
niveau des spécifications, il s'agit d'un langage logique reposant sur
une version simplifiée ad-hoc de la théorie des ensembles. Ce choix est un
peu arbitraire mais peut se justifier par les arguments suivants :
-
il est important
de pouvoir décrire des ensembles, des relations et des fonctions (ce
sont les concepts centraux dans les modélisations objet),
- la théorie des ensembles est bien établie dans la culture
mathématique,
- la théorie des ensembles permet de construire les objets
mathématiques évolués (entiers, arbres, ...)
à partir d'un ensemble réduit de composants de base,
- la théorie des ensembles permet une écriture concise de notions
évoluées.
Nous n'allons pas décrire ici en détail tout le langage de la méthode
B, nous nous contenterons de détailler un petit nombre de concepts
qui nous seront utiles par la suite. Une description plus détaillée
est donnée dans l'annexe A de ce document.
Nous donnons pour chaque notion à la fois la notation
mathématique et une notation ASCII utilisée dans les outils.
2.1 Les expressions
2.1.1 Expressions de base
Parmi les expressions, nous trouvons les constantes entières ainsi que
les variables. Nous trouvons également les expressions formées par
application des opérateurs arithmétiques usuels
(+,-,×,/,mod,...).
Exemple
3 × (n + 3) / k
Remarque
Dans les outils, une variable est formée d'au
moins deux caractères, l'expression précédente s'écrira en fait :
3 * (nn + 3) / kk
2.1.2 Combiner deux expressions
Il est souvent utile de composer deux éléments ensemble pour former
une paire ordonnée. La paire formée des expressions e1 et e2 est
notée e1,e2 ou bien e1 |® e2. Cette seconde
notation sera utilisée le plus souvent lorsque la paire représente un
élément d'une fonction.
Exemple
x |® x+2 représente la paire (x,x+2) et
l'ensemble des paires x |® x+2 pour tous les x entiers
représente la fonction qui à x associe x+2.
2.1.3 Les ensembles
Le langage de B permet également de manipuler des ensembles.
Ensembles de base
|
|
| Ø |
{} |
L'ensemble vide |
| N |
NAT |
L'ensemble des entiers naturels |
| Z |
INTEGER |
L'ensemble des entiers relatifs |
| INT |
INT |
L'ensemble des entiers relatifs compris entre MININT
et MAXINT |
| {e} |
{e} |
L'ensemble réduit à un
élément e |
| {e1,...,en} |
{e1,...,en} |
L'ensemble composé des éléments e1,...,en |
|
Exemple
{1,2,3} est un ensemble.
{Ø} est un ensemble composé d'un élément.
Compréhension
Soit P une formule, on peut définir un ensemble par
compréhension comme l'ensemble de
tous les objets qui vérifient la formule
P. On note cet ensemble {z | P }.
2.1.4 Autres constructions
Quelques autres constructions primitives nous seront utiles.
|
|
| n1..n2 |
(n1..n2) |
L'ensemble des entiers compris entre
n1 et n2 (inclus) avec n1 et n2 des expressions représentants des entiers
positifs. |
| card(E) |
card(E) |
Le cardinal (nombre d'éléments) d'un
ensemble E fini. |
|
2.2 Les formules
2.2.1 Formules de base
On peut utiliser dans B tous les connecteurs logiques de base à
savoir ceux du calcul des prédicats du premier ordre avec égalité.
Le tableau suivant introduit les formules atomiques :
e1 et e2 représentent des expressions
quelconques (entiers, ensembles, paires ...), n1 et n2
sont des expressions qui représentent des entiers.
|
|
| math & ASCII |
| e1=e2 |
| n1 > n2 |
| n1 < n2 |
|
|
| math |
ASCII |
| e1¹e2 |
e1 /= e2 |
| n1 ³ n2 |
n1 >= n2 |
| n1 £ n2 |
n1 =< n2 |
|
2.2.2 Formules ensemblistes
Une formule atomique particulière importante est la formule qui dit
qu'une expression appartient à un ensemble. Nous avons également des
notations pour indiquer les relations d'inclusion ou de non inclusion.
Dans le tableau suivant, e représente une expression tandis que E,
E1 et E2 représentent des ensembles.
| math |
ASCII |
|
| e Î E |
e:E |
L'expression e est un objet de l'ensemble E |
| e ÏE |
e/:E |
L'expression e n'est pas
un objet de l'ensemble E. |
| E1 Í E2 |
E1 <: E2 |
E1 est un sous-ensemble
de E2. |
| ¬ E1 Í E2 |
E1 /<: E2 |
E1 n'est pas un sous-ensemble
de E2. |
2.2.3 Formules composées
Le tableau suivant introduit les formules composées :
F, F1 et F2 représentent des formules.
| math |
ASCII |
| ¬ F |
not(F) |
négation |
| F1 Ù F2 |
F1 & F2 |
conjonction |
| F1 Ú F2 |
F1 or F2 |
disjonction |
| F1 Þ F2 |
F1 => F2 |
implication |
| F1 Û F2 |
F1 <=> F2 |
équivalence |
| $ var . F |
# var . F |
quantification existentielle |
| " var . F |
! var . F |
quantification universelle |
Quantification multiple
Une particularité de B est que la quantification peut avoir lieu
simultanément sur plusieurs variables, elles sont alors entourées de
parenthèses et séparées par des virgules.
Ainsi, on peut écrire la formule suivante :
" (x,y) . (x=y Þ y =x)
qui est équivalente à " x . " y . (x=y Þ y=x)
2.2.4 Les formules bien typées
Dans le langage B, les ensembles servent à contraindre les données; en
ce sens ils jouent le rôle des sortes ou des types d'autres
langages. Cependant, il est en général indécidable de savoir si un
objet e appartient à un ensemble E. En effet vérifier que
e Î {z|P(z)} est équivalent à vérifier que P(e) est vrai, or
la formule P est arbitraire. Cependant, le langage B propose
un système rudimentaire de typage qui permet de distinguer les
entiers, les paires, les ensembles ...
N est un type, les machines pourront
également être paramétrés par des variables représentant des
ensembles arbitraires. Ces variables sont également des types.
Si T1 et T2 sont des types, il en est de
même du produit cartésien de T1 et de T2, noté T1 × T2
qui est le type des paires (t1,t2) d'éléments t1 de type T1
et t2 de type T2. Si T est un type, il en est de même du type
des sous-ensembles de T noté P(T). Ainsi si eiÎ T pour
i=1..n, alors {e1,...,en} Î P(T).
Le langage de B impose que les formules écrites soient bien
"typées". Cela permet d'empêcher a priori de construire des
expressions qui ne représentent effectivement pas des ensembles comme
{x| x Ïx}. Pour cela on impose que chaque variable
introduite soit contrainte à vivre dans un certain ensemble et que ces
ensembles s'organisent de manière cohérente.
Les quantifications universelles, existentielles ainsi que les
constructions d'ensemble par compréhension auront donc
toujours la forme suivante :
" var . P Þ Q $ var . P Ù Q
{var | P Ù Q}
avec P une formule qui contraint chacune des variables z de var. Par
exemple z=e, z Î E, z Í E ou z Ì E
avec z qui n'apparaît ni
dans e ni dans E.
Il faut vérifier que les opérations ensemblistes apparaissant dans la
formule sont compatibles avec la hiérarchie. Par exemple si on a
x=y alors les types de x et de y doivent être égaux. Dans la
relation xÎ X on doit vérifier que X est de type P(U) pour
un certain type U et que x est de type U. Si on a X Í
Y, on doit vérifier que X et Y sont de type P(U) pour un
certain type U.
Exemple
Nous illustrons la procédure de vérification sur un exemple. On
suppose qu'un ensemble E arbitraire est donné.
Soit la formule :
" (a,b). (a,b) Î P(E) × P(E) Þ {x | x Î E
Ù x Î a Ù x Î b } Í E
Comme E est un ensemble paramétrique, les types sont de la forme
P(E), E × E, E × P(E),...
On a a de type P(E), b de type P(E), x de type E on
vérifie que xÎ a et xÎ b sont des formules bien typées et
{x | x Î E Ù x Î a Ù x Î b } est de type P(E),
de même E est de type P(E), donc l'inclusion est bien formée.
2.3 Substitution élémentaire
Une notion importante du langage de B est l'opération d'une
substitution S sur une formule P qui est notée [S]P.
Une substitution élémentaire est de la forme var:=E. Dans
ce cas [var:=E]P représente juste le résultat de la
substitution des occurrences libres de var dans P par
E.
Exemple
[n:=3]n>m est égal à 3>m.
2.3.1 Variables liées et substitution
Les quantificateurs ont la propriété de lier les variables qu'ils
introduisent, c'est-à-dire que le nom de la variable n'intervient plus
dans le sens de la formule, seuls les emplacements (on parle
d'occurrences) où la variable apparaît dans la formule sont importants.
Ainsi n = 4 et m=4 sont des formules différentes mais
$ n.n=4 et $ m.m=4 représentent la même formule.
La variable z est liée dans les formules " z.Q et $
z.Q ainsi que dans l'expression {z| Q}.
Un même nom de variable peut avoir simultanément des occurrences
libres et des occurrences liées dans une formule :
n>0 Þ " n.n ³ 0
Lors de la substitution [var:=E]P, il faut être attentif à
ne remplacer que les occurrences libres de var dans
P et de plus, il ne faut pas que les variables libres de E se
retrouvent liées par des quantificateurs de P
Exemple
Soit la formule P définie comme étant n>0 Þ " n.$ m. m ³ n
On souhaite calculer [n:=m+1]P.
Une opération naïve de remplacement donnerait le résultat erroné :
m+1>0 Þ " n.$ m. m ³ m+1
En renommant les variables liées de P on obtient une formulation
équivalente de P:
n>0 Þ " n0.$ m0. m0 ³ n0
Il est alors licite de calculer la substitution comme un simple
remplacement et on obtient le résultat correct suivant :
m+1>0 Þ " n0.$ m0. m0 ³ n0
Principe de la substitution
Pour calculer le résultat d'une
substitution [var:=E]P on renomme les variables liées de
P de manière à ce qu'elles soient différentes des variables libres
de P et de E puis on procède à un remplacement de var par
E dans la formule ainsi obtenue.
2.3.2 Substitutions multiples
Il est possible de substituer de manière simultanée plusieurs
variables dans une formule. On notera cette opération
[x1,...,xn:=e1,...,en]P
Toutes les variables xi doivent être distinctes.
Une substitution multiple peut alternativement être notée :
x1 :=e1 || ... || xn:=en
Remarque
La substitution
est simultanée, en particulier [x,y:=a,b]P n'est pas équivalent à
[x:=a][y:=b]P.
L'exemple suivant illustre ce phénomène :
[x,y:=y,x]x=y º y=x [x:=y][y:=x]x=y º [x:=y]x=x
º y=y
2.3.3 Substitutions généralisées
Le langage B permet de décrire des substitutions généralisées qui
serviront à représenter des programmes. Celles-ci sont décrites dans
la section 3.
2.4 Les relations et fonctions
En théorie des ensembles, les relations sont un cas particulier
d'ensemble (des ensembles de paires) et les fonctions sont un cas
particulier de relations. Cependant ces concepts essentiels bénéficient
de notations spécifiques que nous décrivons ici.
2.4.1 Relations
Dans le tableau suivant, E, E1 et E2 représentent des ensembles
tandis que R, R1 et R2 représentent des relations.
|
|
| E1 « E2 |
E1 <-> E2 |
L'ensemble des relations entre
éléments de E1 et de E2 |
| |
|
P(E1× E2) |
| R1;R2 |
R1 ; R2 |
Composition des relations R1 et R2 |
| |
|
(x,y) Î (R1;R2) Û $ z. ((x,z) Î R1 Ù (z,y) Î
R2) |
| id(E) |
id(E) |
la relation identité sur l'ensemble
E |
| R-1 |
R~ |
relation inverse de R |
| |
|
(x,y) Î R-1 Û (y,x) Î R |
| E <| R |
E <| R |
la restriction de la relation R au
domaine E |
| |
|
(x,y) Î (E <| R) Û (x Î E Ù (x,y) Î R) |
| R |> E |
R |> E |
la restriction de la relation R à
l'image E |
| |
|
(x,y) Î (R |> E) Û ((x,y) Î RÙ y Î E ) |
|
Ensembles définis à partir de relations
(A.4.1)
|
|
| dom(R) |
dom(R) |
le domaine de la relation R |
| |
|
x Î dom(R) Û ($ y. (x,y)Î R) |
| ran(R) |
ran(R) |
l'image de la relation R |
| |
|
y Î ran(R) Û ($ x. (x,y)Î R) |
|
2.4.2 Fonctions
Les fonctions du système B sont, comme en mathématique,
des cas particuliers de relations.
Une fonction de E1 dans E2 est une relation binaire sur E1
× E2, c'est-à-dire un ensemble de couples (x,y) aussi notés
x|® y. Une relation R est dite fonctionnelle si
lorsque x |® y1 Î R et x |® y2 Î R alors
y1=y2. Une fonction f de E1 dans E2 est une relation
fonctionnelle. L'ensemble des relations fonctionnelles de E1 dans
E2 est noté E1 +-> E2. Le domaine d'une fonction f
est l'ensemble dom(f) des x pour lesquels il existe y tel
que x |® y Î f. Si x est dans le domaine de f alors on
note f(x) l'unique y tel que x |® y Î f.
Une fonction est totale si son domaine est égal à l'ensemble E1
tout entier.
D'autres notions sur les fonctions sont définies en A.4.2.
2.4.3 Séquences
Les séquences sont des suites ordonnées d'objets d'un ensemble E.
Une manière de les modéliser mathématiquement est de les voir comme
des fonctions de N dans E dont le domaine est soit l'ensemble
vide (dans le cas de la séquence vide) soit l'ensemble 1..n pour n
un entier strictement positif. L'ensemble des séquences sur E est
noté seq(E), les principales constructions sur les
séquences sont rappelées en annexe (A.4.3).
Finalement, nous pouvons introduire des constantes correspondant à des
chaînes de caractères écrites entre guillemets comme "Hello".
2.4.4 Exemple
Les notions que nous avons introduites sont suffisantes pour modéliser
un petit problème.
On s'intéresse à un ensemble de personnes et leurs
liens de parenté et de mariage.
On suppose donné un ensemble personnes représentant les
personnes. On cherche à modéliser de manière ensembliste les notions
de femmes, hommes, les relations de
a_pour_epoux, a_pour_épouse, a_pour_mère,
a_pour_père,
a_pour_frère, a_pour_enfant, est_marié_à
sachant que les principes suivants doivent être respectés :
-
chaque personne est soit un homme soit une femme,
- nulle personne n'est à la fois homme et femme,
- seules les femmes ont des époux qui sont des hommes,
- chaque femme a au plus un mari qui n'est le mari d'aucune autre femme,
- une mère est une femme mariée,
- le père est l'époux de la mère.
On identifie les données minimales qui doivent être primitives (par
exemple l'ensemble hommes, les relations
a_pour_epoux et a_pour_mère).
Les contraintes imposent des restrictions sur la nature de ces objets.
On peut ensuite définir les autres notions en fonction des notions
primitives.
-
hommesÍ personnes
- femmes = { p | p Î personnes Ù p Ï hommes}
- a_pour_epoux Î femmes × hommes
- a_pour_epoux est une fonction (partielle) de femmes
dans hommes :
a_pour_epoux Î femmes +->
hommes ce qui signifie :
(f |® h1 Î a_pour_epoux Ù
f |® h2 Î a_pour_epoux) Þ h1=h2
- a_pour_epoux est une fonction injective de femmes
dans hommes :
a_pour_epoux Î femmes >+>
hommes ce qui signifie :
(f1 |® h Î a_pour_epoux Ù
f2 |® h Î a_pour_epoux) Þ f1=f2
- a_pour_epouse est la fonction inverse de
a_pour_epoux :
a_pour_epouse Î hommes>+>femmes et
a_pour_epouse=a_pour_epoux-1 ce qui signifie :
m |® f Î a_pour_epouse Û
f |® m Î a_pour_epoux
- a_pour_mère est une fonction (partielle) de personnes
dans femmes :
a_pour_mère Î personnes +-> femmes
- a_pour_père est une fonction (partielle) de personnes
dans hommes qui est la composition de la relation
a_pour_mère et de la relation : a_pour_epoux
a_pour_père =a_pour_mère;a_pour_epoux ce qui
signifie :
x |® p Î a_pour_père Û ($ m.
x |® m Î a_pour_mère Ù m |® p Î
a_pour_epoux)
- a_pour_enfant est une relation de personnes «
personnes, c'est la réunion des relations inverses de
a_pour_mère et a_pour_père :
a_pour_enfant = a_pour_mère-1 È
a_pour_père-1 ce qui signifie :
x |® y Î a_pour_enfant Û
(y |® x Î a_pour_mere Ú
y |® x Î a_pour_pere)
- a_pour_frère est une relation de personnes «
hommes. Pour trouver les frères, il faut chercher la mère
puis composer avec les enfants de cette mère qui sont des hommes et
qui ne sont pas la personne initiale. Cela donne :
a_pour_frère = ((a_pour_mère ; a_pour_mère-1)
|> hommes) - id(hommes)
Le système B privilégie l'utilisation de symboles algébriques pour
représenter les contraintes sur les données sans introduire de quantificateur.
Cela permet d'automatiser plus simplement les preuves.
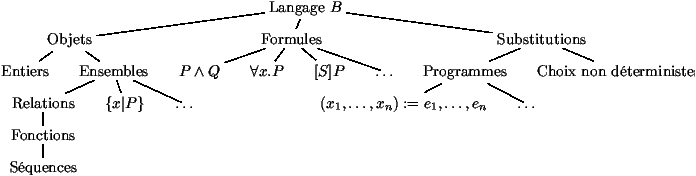
Ce qu'il faut retenir
Le langage associé à la méthode B permet de manipuler différentes
classes d'objet :
2.5 Méthodes de preuve
2.5.1 Raisonner sur les objets
Nous n'avons donné aucun système d'axiomes pour raisonner sur les
objets introduits. Un tel système peut se trouver dans le livre "The
B-Book" de J.-R. Abrial. Cependant une présentation effectuée de
manière rigoureuse est très fastidieuse. Pour ce cours, il est
suffisant de raisonner de manière semi-formelle, comme on peut le faire
en mathématiques.
2.5.2 Raisonner sur les programmes
Dès lors qu'on connaît ce qui est attendu d'un programme (sa
spécification) et qu'on connaît la manière dont le programme va
s'exécuter (sa sémantique), il est possible de faire une
preuve de correction du programme.
2.5.3 Logique de Hoare
Hoare dès les années 70, puis Floyd et Dijkstra ont développé l'idée
qu'il fallait prouver les programmes. Pour pouvoir raisonner sur un
programme, il faut savoir les représenter et se donner des règles et
méthodes de preuve sur ces objets.
Modélisation du programme
L'exécution d'un programme transforme l'état de la mémoire de la
machine. La partie qui nous intéresse correspond aux valeurs associées
aux variables du programme. On représente souvent l'environnement
d'exécution du programme comme une fonction qui à chaque variable du
programme associe une valeur (entier, chaîne de caractères,
ensemble fini,...)
Il n'est pas raisonnable de raisonner globalement sur le programme
comme une transformation de l'état de la mémoire.
Hoare a donc proposé ce qui est connu comme la
sémantique axiomatique ou la logique de Hoare.
L'idée principale de la logique de Hoare, est de ne pas raisonner sur
la mémoire globalement mais seulement sur les valeurs des variables
apparaissant dans le programme.
Si en un point du programme, je démontre qu'une propriété P(x) est
vérifiée, cela signifie que la propriété P(v) est vraie, avec v la
valeur associée à la variable x dans la mémoire à ce point
d'exécution du programme.
Exemple
Que fait le programme suivant ? Comment le démontrer ?
n:=5;
i:=n; res:=1;
while i > 0 do res:=i*res; i:=i-1 end
print(res)
La logique de Hoare établit un système de déduction qui permet de
démontrer des triplets de Hoare
{f}P{y}
dans lesquels P est un programme et f et y sont des
formules portant sur les variables du programme.
Lorsqu'un triplet {f}P{y} est vrai cela signifie que si
les valeurs des variables de P satisfont la formule {f}
alors après l'exécution de P, les nouvelles valeurs de ces variables
satisferont la propriété y.
Exemple-suite
On peut annoter le programme précédent par des assertions
n:=5;
{n³ 0}
i:=n; res:=1;
{res*i!=n!}
while i > 0 do res:=i*res; i:=i-1 end
{i=0 Ù res=n!*i!}
print(res) {res=n!}
Un programme vu comme un transformateur de prédicat
La logique de Hoare permet de voir les programmes non plus comme des
fonctions qui transforment les états de la mémoire mais comme des
transformateurs de prédicats. Si on se donne un programme P
et une propriété y portant sur les variables de P alors on peut
définir en fonction de P la plus faible condition f
pour que {f}P{y} soit vérifié. On note
wp(P,y) la propriété f ainsi définie.
Elle doit vérifier les deux conditions suivantes :
{wp(P,y)}P{y}
" f.{f}P{y} Þ (f Þ wp(P,y))
Les règles de la logique de Hoare permettent de calculer
effectivement wp(P,y) pour un y quelconque en fonction de
P, lorsque P ne contient pas de boucle. Par exemple :
| wp(x:=e,y)=y[x¬ e] |
| wp(if C then P else Q end,y)
= (C Þ wp(P,y)) Ù (¬ C Þ wp(Q,y)) |
| wp(P1;P2,y)
= wp(P1,wp(P2,y)) |
Le cas des boucles
L'introduction de boucles dans les programmes complique le
raisonnement. Il est nécessaire de produire un invariant qui
est une propriété qui sera vérifiée à l'entrée dans la boucle et
préservée par le corps de la boucle. D'autre part, une boucle peut ne
pas terminer. On distingue alors deux variantes de la logique de Hoare
que l'on qualifie de partielle et totale.
-
La logique de Hoare partielle ne garantit pas la
terminaison; le triplet {f}P{y} s'interprète comme :
si f est vérifié dans l'état initial et si P termine alors
y est vérifié dans l'état final. En particulier la formule
{f}P{false} est équivalente à P ne termine jamais
à partir d'un état satisfaisant f.
- La logique de Hoare totale garantit la terminaison; le
triplet {f}P{y} s'interprète comme : si f est
vérifié dans l'état initial alors P termine et y est vérifié
dans l'état final. En particulier la formule
{f}P{true} est équivalente à P termine toujours à
partir d'un état satisfaisant f..
Des exemples de logique de Hoare seront développés en
exercice (1).









