1. Spécifier les types abstraits point et vecteur.
type point
{constructeurs}
{ l'origine (0, 0) }
origine : point
{ construit un point à partir de ses coordonnées x,y}
consPoint : réel x réel -> point
{opérations}
{ translation d'un point par un vecteur}
translate : point x vecteur -> point
{ distance entre deux points }
distance : point x point -> réel
{ test d'égalité }
égale : point x point -> booléen
fin
type vecteur
{constructeurs}
{ le vecteur nul }
vecteurNul : vecteur
{ construit le vecteur PQ à partir des points P et Q}
pointVec : point x point -> vecteur
{ construit un vecteur à partir de ses coordonnées }
consVec : réel x réel -> vecteur
{opérations}
{ norme d'un vecteur, sqrt (x^2 + y^2) }
norme : vecteur -> réel
{ multiplication d'un vecteur par un scalaire, k.V }
mulVec : réel x vecteur -> vecteur
{ produit scalaire de deux vecteurs, x1y1 + x2y2}
scalaire : vecteur x vecteur -> réel
{ vecteur (-y, x), orthogonal au vecteur (x, y) }
ortho : vecteur -> vecteur
{ test de colinéarite, V1 = k.V2 }
colinéaire : vecteur x vecteur -> booléen
fin
type droite
{constucteur}
consDroite : point x vecteur -> droite
{opérations}
pointSurDroite : point x droite -> booléen
parallèle : droite x droite -> booléen
droiteOrtho : droite x point -> droite
fin
{réalisation :}
type droite = produit
origine : point
direction : vecteur
fin
fonction consDroite (p: point, v: vecteur) -> droite
{ construit une droite à partir d'un point p et
d'un vecteur v, qui doit être non nul. }
lexique
d : droite
début
d.origine <- p
d.direction <- v
retourner d
fin
fonction pointSurDroite (p: point, d: droite) -> booléen
{ teste si le point p est sur la droite d}
début
retourner
colinéaire (d.direction, pointVec(d.origine, p))
fin
fonction parallèle (d1, d2 : droite) -> booléen
{ teste si deux droites sont parallèles }
début
retourner colinéaire (d1.direction, d2.direction)
fin
fonction droiteOrtho (d : droite, p : point) -> droite
{ calcule la droite orthogonale a d passant par p }
début
retourner consDroite (p, ortho (d.direction))
fin
3. Fonction qui calcule où se trouve un point M par rapport à une droite D.
type côté = (aGauche, aDroite, dessus)
fonction quelCôté (p : point, d : droite) -> côté
{ calcule la position relative de p par rapport à d }
lexique
pm : vecteur
s : réel
début
pm <- pointVec (d.origine, p)
s <- scalaire (ortho (d.direction), pm)
selon le cas
s > 0 : retourner aGauche
s = 0 : retourner dessus
s < 0 : retourner aDroite
fin
fin
4.a Spécifier le type abstrait polygone.
{ type permettant de représenter un segment de droite }
type segment = produit
p1, p2 : point
fin
type polygone
{constructeur}
{ construction d'un polygone avec 3 points }
triangle : point x point x point -> polygone
{opérations}
{ ajout d'un point à un polygone }
action ajouterPoint : DR polygone x point
{ retourne le i-ème point du polygone }
ièmePoint : polygone x entier -> point
{ retourne le i-ème segment du polygone }
ièmeSegment : polygone x entier -> segment
fin
4.b Réaliser le type polygone.
const maxp = 100
{ un polygone est constitué d'un tableau de points et
d'un nombre de points }
type polygone = produit
pts : tableau [0 .. maxp] de point
nbp : entier
fin
fonction triangle (p1, p2, p3 : point) -> polygone
{ crée un polygone à partir de 3 points }
lexique
poly : polygone
début
poly.pts [0] <- p1
poly.pts [1] <- p2
poly.pts [2] <- p3
poly.nbp <- 3
retourner poly
fin
action ajouterPoint (DR poly : polygone, p : point)
{ ajoute un point à la fin du polygone si c'est possible }
début
si poly.nbp <= maxp
poly.pts [poly.nbp] <- p
poly.nbp <- poly.nbp + 1
sinon
erreur ("trop de points dans le polygone !")
fin
fonction ièmePoint (poly : polygone, i : entier) -> point
{ retourne le i-ème point du polygone s'il existe }
début
si i >= 0 et i < poly.nbp
retourner poly.pts[i]
sinon
erreur ("point inexistant")
fin
fonction ièmeSegment (poly:polygone, i:entier) -> segment
{ retourne le i-ème segment du polygone s'il existe }
lexique s : segment
début
si i >= 0 et i < poly.nbp
s.p1 <- poly.pts[i]
si i = poly.nbp-1
s.p2 <- poly.pts[i+1] { segment PiPi+1}
sinon
s.p2 <- poly.pts[0] { segment PnP0 }
sinon
erreur ("segment inexistant")
retourner s
fin
5. Spécifier et réaliser une fonction qui calcule si un polygone est convexe.
fonction segDroite (s : segment) -> droite
{ retourne la droite support du segment s }
début
retourner consDroite (s.p1, pointVec (s.p1, s.p2))
fin
fonction convexe (poly : polygone) -> booléen
{ calcule si un polygone est convexe. On suppose que trois
points successifs du polygone ne sont jamais alignés }
lexique
seg : droite
c, c1 : côté
i, j : entier
début
pour i parcourant [0..poly.nbp -1]
début
{ trouver la droite support du ième segment }
s <- segDroite (ièmeSegment (poly, i))
{ regarder de quel côté est le point suivant }
j <- (i + 1) mod poly.nbp
c <- quelCôté (ièmePoint (poly, j), seg)
{ regarder tous les points et vérifier qu'ils
sont du même côté que c }
pour j parcourant [0..poly.nbp -1]
début
c1 <- quelCôté (ièmePoint(poly, j), seg)
si c1 != c
retourner faux
fin
fin
retourner vrai
fin
1. Spécifier et réaliser la fonction permettant d'additionner deux GrandNombre.
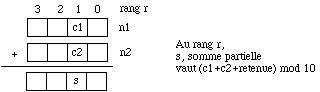
fonction somme (n1, n2 : GrandNombre) -> GrandNombre
{ calcule la somme de deux grands nombres }
lexique
résultat : GrandNombre
retenue : chiffre
s, r, rmax : entier
début
résultat <- zéro
retenue <- 0
{ r est le rang pour lequel on calcule la somme }
r <- 0
{ rmax est le nombre maximal de chiffres de n1 et n2}
rmax <- max (nbChiffres(n1), nbChiffres(n2))
pour r parcourant [0 .. rmax]
début
{ calculer la somme partielle }
s <- ième(r, n1) + ième(r, n2) + retenue
{ calculer la retenue et le chiffre de rang r }
retenue <- s div 10
s <- s mod 10
affecter (résultat , r, s)
fin
{ ne pas oublier la dernière retenue }
affecter (résultat , r, retenue)
retourner résultat
fin
2. Spécifier et réaliser ensuite une fonction qui multiplie deux GrandNombre.
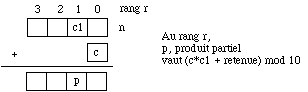
fonction multc (n:GrandNombre, c:chiffre) -> GrandNombre
{ calcule le produit d'un grand nombre par un chiffre }
lexique
résultat : GrandNombre
retenue : chiffre
p, r : entier
début
résultat <- zéro
retenue <- 0
pour r parcourant [0 .. nbChiffres(n)]
début
p <- c * ième (r, n) + retenue
retenue <- p div 10
p <- p mod 10
affecter (résultat, r, p)
fin
affecter (résultat, r, retenue)
retourner résultat
fin
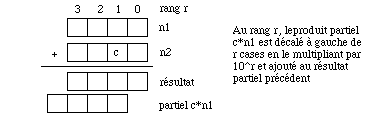
fonction produit (n1, n2 : GrandNombre) -> GrandNombre
{ calcule le produit de deux grands nombres }
lexique
résultat : GrandNombre
partiel : GrandNombre
r : entier
début
résultat <- 0
pour r parcourant [0 .. nbChiffres(n2)]
début
partiel <- multc (n1, ième (r, n2))
partiel <- mul10n (partiel, r)
résultat <- somme (résultat, partiel)
fin
retourner résultat
fin
3. Réaliser les constructeurs et opérations du type abstrait GrandEntier.
const maxc = 100
type GrandNombre = tableau [0 .. maxc] de chiffre
fonction zéro -> GrandNombre
{ retourne le nombre 0 }
lexique
résultat : GrandNombre
i : entier
début
pour i parcourant [0 .. maxc]
résultat [i] <- 0
retourner résultat
fin
action affecter (DR n:GrandNombre, i:entier, c:chiffre)
{ effecte le ième chiffre d'un grand nombre. i doit être
inférieur à maxc, nombre maximal de chiffres}
début
n[i] <- c
fin
fonction nbChiffres (n : GrandNombre) -> entier
{ retourne le nombre de chiffres d'un grand nombre }
lexique
i : entier
début
i <- maxc
tantque i > 0 et n[i] = 0 faire
i <- i - 1
retourner i
fin
fonction mul10n (n:GrandNombre, p:entier) -> GrandNombre
{ multiplie un grand nombre par 10^p, p > 0 }
lexique
résultat : GrandNombre
i : entier
début
{ décaler les chiffres de p rang vers la gauche }
pour i parcourant [0 .. maxc - p]
résultat [p + i] <- n [i]
{ mettre des 0 dans les p premier rangs }
pour i parcourant [0 .. p]
résultat [i] <- 0
retourner résultat
fin