Les mots sont une structure très utilisée en informatique. La théorie des langages classifie les ensembles de mots (langages réguliers ou algébriques) suivant leur propriétés, en particulier la manière de reconnaître qu’un mot appartient à un certain langage. Un programme donné à interpréter à un ordinateur est un mot. De la même manière, on peut représenter les actions réalisées par un programme par un mot, et donc certaines techniques d’analyse de programme s’appuient sur des résultats de théorie des langages.
Les mots sont aussi la notion sous-jacente aux structures séquentielles (tableaux, listes) qui servent dans de nombreux algorithmes en particulier pour représenter en machine des ensembles d’objets.
On se donne un ensemble (en général fini) d’objets A que l’on appelle un alphabet. Les éléments d’un alphabet sont appelés des caractères.
Les mots sont des suites finies de caractères. On peut les représenter comme des couples formés d’un entier n (la taille du mot) et d’une application f de [0,n[ dans A. On notera A* l’ensemble des mots sur l’alphabet A.
Si m est un mot, on note |m| la longueur du mot et pour chaque i < |m|, on note m[i] le i-ème caractère du mot m (on commence à 0).
Pour définir un mot m, il suffit de se donner sa longueur n et une application de [0,n[ dans A.
On introduit les opérations suivantes sur les mots:
On montre les propriétés essentielles des opérations précédentes.
Un mot m qui n’est pas vide a un premier caractère a=m[0] et peut être décomposé m=am′ avec m′ le mot obtenu en retirant le premier caractère de m et défini par : |m′|=|m|−1 et m′[i]=m[i+1]. On introduit les notations hd(m) pour le caractère a et tl(m) pour le mot m′.
Un langage est un ensemble de mots. Il peut se définir par un système d’inférence.
|
|
|
| aabb abb aab abab |
|
|
Le schéma de définition récursive sur les entiers se généralise au cas des mots. Une manière naturelle de définir une application f dans A*→ B consiste à définir la valeur b∈ B de l’application pour le mot vide, et pour un caractère a ∈ A arbitraire et un mot m∈ A* de définir f(am) en fonction de a, de m et de f(m), c’est-à-dire se donner une application G dans A× A* × B → B telle que f(am)=G(a,m,f(m)).
| lg(є)=0 lg(am)=1+lg(m) |
| nb(b,є)=0 nb(b,am)=1+nb(b,m) si a=b nb(b,am)=nb(b,m) si a≠ b |
On remarque que l’on ne peut pas se servir de la concaténation de deux mots arbitraires comme construction d’équations fonctionnelles. En effet si on pose des équations:
| f(є)=0 f(a)=1 f(m1 m2)=1+f(m1)+f(m2) |
alors ces équations n’ont pas de solution en effet on devrait avoir f(aє)=1+f(a)+f(є)=2 et par ailleurs comme aє=a, on a aussi f(aє)=f(a)=1 ce qui ne peut se réaliser. On peut toujours utiliser une définition par cloture de la relation f(x,n) mais cette relation n’est pas fonctionnelle. Cela vient du fait que la décomposition d’un mot m sous la forme m1m2 n’est pas unique.
Les mots sont des structures linéaires. Pour des raisons d’efficacité, on introduit des structures un peu plus complexes qui sont celles d’arbre. Ainsi les fichiers dans un ordinateur sont regroupés dans des répertoires. Un répertoire peut contenir des fichiers mais aussi d’autres répertoires créant ainsi une structure hiérarchique arborescente. Pour retrouver un fichier, il ne sera pas forcément nécessaire de les considérer dans leur globalité : si on sait reconnaitre à chaque étape dans quel sous-réperoire il peut se trouver, la recherche sera proportionnelle à la profondeur d’imbrication (et au nombre de fichiers dans le dernier répertoire), pas au nombre total de fichiers. Nous allons définir ce qu’est formellement un arbre.
Il y a de nombreuses manières de définir la notion d’arbre. Une des plus courantes est de se ramener à la notion de graphe dirigé.
On appelle feuille de l’arbre un sommet dont le degré sortant est nul. Les autres sommets sont appelés des nœuds internes.
La profondeur d’un sommet de l’arbre est la longueur du chemin de la racine à ce sommet. La hauteur de l’arbre est la profondeur maximale d’un sommet (quand elle existe, car on peut construire des arbres ayant des branches infinies).

On appelle père d’un nœud qui n’est pas la racine, le sommet source de l’arête entrante sur ce sommet.
Il y a au moins un sommet de degré entrant 0, si c’est le seul sommet alors il n’y a pas d’arêtes et donc c’est un arbre.
On suppose maintenant le résultat vrai pour un graphe avec n sommets et on le montre pour un graphe à n+1 sommets.
La somme des degrés entrants est égale à la somme des degrés sortants. S’il y a n sommets, la somme des degrés entrants est n−1, dont il y a au moins un sommet x de degré sortant 0. Cela ne peut pas être le sommet de degré entrant 0 car sinon ce serait un point isolé et donc le graphe ne serait pas connecté. Le sommet x a donc un degré entrant de 1. On retire le sommet x du graphe ainsi que l’arête entrante, le graphe obtenu satisfait bien les hypothèses du graphe initial, on peut lui appliquer l’hypothèse de récurrence et c’est donc un arbre. Les seuls chemins qui passent par e sont les chemins qui se terminent par e pour arriver en x, on a donc bien que le graphe complet est un arbre.
On représente souvent les arbres avec une convention implicite sur le sens des flèches (du haut vers le bas ou du bas vers le haut ou encore de gauche à droite), en alignant verticalement ou horizontalement tous les sommets de même profondeur. On se dispense alors de représenter les “noms” des sommets, la position géométrique suffit à donner une représentation canonique de l’arbre.
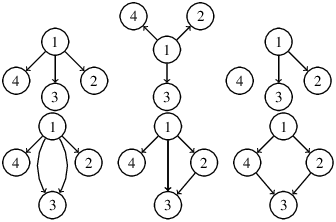
On s’intéresse à des ensembles de mots formés d’entiers naturels non nuls, c’est-à-dire des sous-ensembles de ℕ\{0}*.
Si on se donne un ensemble de positions P alors on peut lui associer un graphe dirigé dont les sommets sont les éléments de P et dans lequel il y a une arète de m à mi pour tout mi∈ P.
La racine correspond au mot vide et est connectée à chacun des sommets m en passant par tous préfixes de m. Le chemin est unique car sinon un mot aurait dex préfixes différents.
Réciproquement, tout arbre ayant un ensemble dénombrable de sommets est isomorphe à un arbre construit à partir d’un ensemble de position.
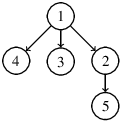
Un arbre vu comme un graphe ou un ensemble de position représente uniquement un squelette. On a remarqué que les noms des sommets n’étaient pas une information très intéressante. L’arbre précédent se représentera tout aussi bien de la manière suivante, chaque nœud pouvant s’identifier grace à sa position.
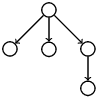
En général, on a besoin d’associer des informations aux nœuds de l’arbre. On le fait en se donnant une application des sommets de l’arbre dans l’ensemble des informations A que l’on souhaite afficher dans l’arbre et on inscrit cette valeur comme étiquette du noeud. Par exemple pour un arbre de classification en biologie ou d’organisation de répertoires,
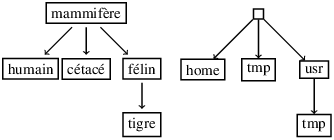
Parfois les annotations ne sont associées qu’aux nœuds internes et pas au feuilles qui sont vues comme des nœuds sans information (ceci est lié à la représentation syntaxique des arbres annotés et à leur représentation en machine).
Nous allons généraliser les constructions introduites précédemment pour les entiers ou les mots à des structures plus complexes. En effet en informatique, la machine manipule in fine des données assez simples à savoir des suites (finies) de 0 et de 1. Néanmoins, lorsqu’on veut modéliser une structure particulière comme une base de données ou une image, ces suites de 0 et de 1 sont organisées suivant des schémas très spécifiques. L’identification de ces schémas va nous permettre d’avoir des moyens de haut niveau pour construire ces objets et raisonner en faisant abstraction de la représentation physique.
On est amené par exemple à manipuler des structures d’arbres, que ce soit des arbres binaires pour représenter efficacement des ensembles finis d’objets ou bien des arbres de syntaxe abstraite pour représenter des programmes dans les compilateurs.
Dans cette section, on s’intéresse à des représentations syntaxiques, qu’il faut bien distinguer du modèle sous-jacent. Par exemple si on considère l’expression 2+3, le niveau syntaxique fait une différence entre cette expression et les expressions 5, 3+2 ou 2+(2+1) alors que toutes ces expressions correspondent au même modèle entier 5. Cette distinction entre syntaxe et modèle réel est importante en informatique où l’ordinateur effectue des manipulations symboliques sur des objets structurés qui représentent des notions complexes (des nombres flottants voir des rationnels ou des réels, des bases de données, des programmes, …).
|
|
On utilise parfois une notation infixe pour les symboles de fonctions binaires, c’est-à-dire que l’on écrira (t1 f t2) au lieu de f(t1,t2) de même on peut omettre certaines parenthèses en s’appuyant sur des conventions, mais il s’agit de facilités d’écriture qui ne changent pas la définition mathématique.
En logique ou en informatique on a souvent besoin de considérer des termes généralisés dans lesquels apparaissent des variables. On l’a vu avec les formules quantifiées en logique. En informatique, les fonctions dans les langages de programmation correspondent à des termes avec des variables (pour les paramètres). Contrairement aux constantes dans les signatures, les variables peuvent être choisies dans un ensemble infini X (mais seulement un nombre fini de variables apparait dans chaque terme).
|
|
|
Les termes de T( F) sont un cas particulier de terme avec variables dans lesquels l’ensemble des variables X est vide. Dans la suite, on considèrera uniquement des termes sans variables.
L’égalité sur les mots induit une égalité sur les termes. En particulier on peut dériver la propriété suivante :
| t=u ⇔ |
|
On peut généraliser la notion de définition récursive d’une application sur les entiers en définition récursive sur des termes arbitraires.
On suppose que l’on veut définir une application F dans T( F) → A. Pour cela on va se donner les objets suivants :
| × |
| → A | ||||||||||||||||||||||||||||||||||||
Il existe une unique application F dans T( F) → A qui vérifie :
| F(c)=dc (c∈ F0) F(f(t1,…,tn))=Gf(t1,…,tn,F(t1),…,F(tn)) (f∈ Fn) |
Le fait que l’on puisse définir une telle application est une conséquence de l’égalité sur les termes. En particulier, deux termes qui débutent par des symboles différents sont différents.
En effet ce schéma permet de définir une application f telle que f(c)=1 pour les constantes et f(t)=2 pour tous les termes qui commencent par un symbole de fonction. Si on avait plus(0,0)=0 alors on en déduirait f(plus(0,0))=f(0) et donc 2=1.
L’induction généralisée associée à la définition par cloture de T( F) s’exprime de la manière suivante. Soit P(t) une propriété qui dépend d’un terme t ∈ T( F). On suppose :
alors ∀ t ∈ T( F),P(t).
| ∀ t ∈ T( F),ht(t) ≤ size(t) |
| ht(f(t1,…,tn))= |
|
Nous avons défini les termes comme des mots en mettant en avant la structure séquentielle ce qui nous a amené à introduire les symboles parenthèses et virgule. La définition par cloture met l’accent sur la structure arborescente des termes. Une constante est vue comme une feuille de l’arbre, un terme f(t1,…,tn) est représenté comme un arbre dont la racine est étiquetée par f et qui a n fils, que l’on considère de manière ordonnée. Le i-ème sous-arbre est associé au terme ti.
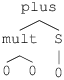
Un terme définit un ensemble de positions. Une position est une suite finie d’entiers compris entre 1 et l’arité maximale des éléments de la signature. La position décrit un chemin pour se déplacer dans l’arbre en partant de la racine, l’entier permet de choisir dans quel sous-terme continuer.
|
|
On remarque que lorsque t est une constante alors: pos(t)={є }.
| t|є=t f(t1,…,tn)|im=ti|m |
Lorsque l’on introduit des signatures complexes, il est souvent naturel de distinguer différentes catégories de termes.
Par exemple les termes correspondant aux suites finies peuvent se construire avec une constante nil et un symbole cons binaire pour ajouter un caractère en premier élément d’une suite. Il nous reste à introduire une signature pour représenter les éléments de la suite, par exemple des entiers avec une constante 0 et un symbole unaire S. Dans le cadre général, rien n’interdit de construire des termes comme S(cons(0,є)) qui n’ont pas d’interprétation naturelle.
Pour remédier à ce problème, on introduit des sortes qui permettent de distinguer les différentes classes de termes. Les sortes sont un ensemble fini (par exemple {nat,seq } pour représenter la sorte des entiers naturels et celle des séquences d’entiers). Au lieu d’être un simple entier décrivant le nombre d’arguments, une arité décrit la sorte des termes que le symbole prend en argument et la sorte du terme construit en résultat, on l’écrira s1×…× sn → s. Dans notre exemple de suite d’entiers :
On définit maintenant par cloture l’ensemble T( F,s) des termes de sorte s:
|
Une structure importante en informatique est celle d’arbre binaire. On suppose que l’on souhaite stocker dans cet arbre des objets. On introduit une sorte elt pour représenter ce qui est stocké dans l’arbre avec par exemples des constantes a, b, c, d, e. On introduit également la sorte tree pour les arbres binaires.
Une signature (notée A) possible est donnée par :
L’arbre
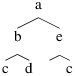 |
est représenté par le terme :
node(node(node(leaf,c,leaf), b, node(leaf,d,leaf) ,a,node(leaf,e,node(leaf,c,leaf))))
qui lui même peut se représenter sous forme d’arbre :
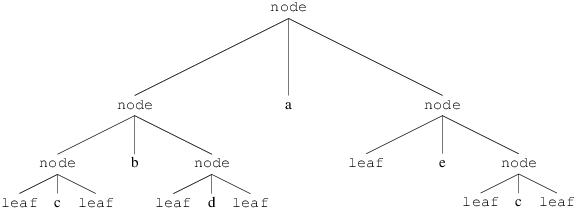
On définit de nombreuses fonctions sur les arbres en suivant le schéma de définition récursive sur les termes.
Par exemple la hauteur:
| ht(leaf) = 0 ht(node(l,a,r)) = 1 + max(ht(l),ht(r)) |
On peut aussi définir un parcours d’arbre qui construit la suite finie des éléments qui apparaissent dans l’arbre :
| elts(leaf) = є elts(node(l,a,r)) = elts(l) a elts(r) |
De manière générale, le principe de définition récursive sur les arbres est donné par la définition suivante :
Soit une fonction h∈ X → Y et g∈ T × E × T × Y × Y × X → Y alors il existe une unique fonction f∈ T × X → Y telle que :
| f(leaf,x)=h(x) f(node(l,e,r),x)=g(l,e,r,f(l,x),f(r,x)) |
De plus la propriété suivante (schéma d’induction sur les arbres) est vérifiée pour toute propriété P sur les arbres :
Comme précédemment, le schéma peut être généralisé en autorisant dans les appels récursifs de f(l,x) et f(r,x) d’appliquer une transformation à x.
Preuve: La fonction demandée est la solution des équations :
| sum(leaf)=0 sum(node(l,e,r))=sum(l)+e+sum(r) |
□