Deep Learning in Practice

Chapter 7: Small data, weak supervision, robustness / Modeling: incorporating priors or physics

• Small data
• Weak supervision, self-supervision
• Multi-task and transfer learning
• Data augmentation, synthetic data, invariances

• Curriculum learning (from easy task to harder task)
• Example of invariance enforcement by design: permutation invariance
  • Deep Sets
  • Examples of applications: when dealing with unordered set of points
  • Equivariance to rotations
• Learning the invariance
• Choosing physically meaningful metrics
  • Optimal transport (Sinkhorn approximation)
  • Metric learning: Siamese networks
• Noisy data (can be seen as noise modeling)
  • Denoising auto-encoder
  • What if noise is already present in the dataset, but unknown? (no denoised target available)
• Incorporating physical knowledge: Example of learning dynamics equations
  • Data assimilation
  • Learning a PDE (equation not known)
  • Incorporating invariances/symmetries of the problem
  • Knowing an equation that the solution has to satisfy : solving PDEs!
  • Important example in chemistry
  • Form of the solution known
  • In practice
• Deep for physic dynamics : learning and controlling the dynamics
• Combining deep learning & classical approaches (data term + regularizer)

I - Small data, weak supervision, robustness

Small data

Weak supervision, self-supervision

Multi-task and transfer learning

Data augmentation, synthetic data, invariances

II - Modeling: incorporating priors or physics

Curriculum learning (from easy task to harder task)

• Main idea: not harder "tasks", but harder "examples": pick gradually harder and harder examples, i.e. make the probability of picking hard examples to increase with time
• Formalization: instead of training directly on the distribution $p$ of all examples, train on a distribution $q_t$ varying with time and including gradually harder examples more frequently:
  • at time $t \in [0,1]$, consider the distribution $q_t(z) = w_t(z) p(z)$ over all examples $z$
  • with $w_t$ increasing with $t$, for each $z$ (i.e., starting from few examples and adding some with time)
  • and entropy $H(q_t)$ increasing with $t$ (i.e., more and more diversity)
  • and $w_t = 1$ for all $z$, i.e. final distribution $q_1(z) =$ target $p(z)$
• NB: notion of "easy"/"hard" example = defined by hand by the user
• Experiments:
  • classifying geometrical shapes (triangles, rectangles...) from easy shapes to more complex ones
  • NLP task with growing vocabulary
    $\implies$ notice faster & better convergence

• when the task consists in predicting long-term trajectories (time sequences): first learn to predict next time step, then when achieved, next next time step, etc. i.e. progressively grow the prediction time span
• this is needed, as gradients of errors (w.r.t. parameters of a recurrent network) in long time series will not be informative (= dominated by kind-of-random terms) as long as shorter-span predictions are not already sufficiently good.

Example of invariance enforcement by design: permutation invariance

Deep Sets

• invariant par construction
• theorem: universal approximator (2-steps formulation)
• theorem 2: idem, for stacks of simple equivariant/invariant layers
  [Mixed batches and symmetric discriminators for GAN training; Thomas Lucas, Corentin Tallec, Jakob Verbeek, Yann Ollivier; ICML 2018]

Examples of applications: when dealing with unordered set of points

• PointNet / PointNet++ : 3D point cloud classification / segmentation (e.g., shapes obtained by laser measurements)
  • [PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation; Charles R. Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas; CVPR 2017]
  • [PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space; Charles R. Qi, Li Yi, Hao Su, Leonidas J. Guibas; NIPS 2017]
    
• mini-batch GAN (see above)
• deep genetics
  [End-to-End Deep Learning Approach for Demographic History Inference; Théophile Sanchez, Guillaume Charpiat, Flora Jay; Human Evolution: Fossils, Ancient and Modern Genomes 2017]

Equivariance to rotations

• Easy, simplistic way:
  • [E(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials; Simon Batzner et al; 2021]
  • Architecture = succession of rotation-equivariant blocks, each of which proceeds as follows:
  • Decompose a vector $v$ in its norm $n = \|v\|$ and its direction $d = \frac{v}{\|v\|}$; work on the norm and recombine: $f(n) d$, i.e. $f(\|v\|) \frac{v}{\|v\|}$
• The hard, theoretical physicist way:
  • Use spherical harmonics and Clebsch-Gordan coefficients, a mathematical framework precisely developped for (in particular) 3D rotation equivariance.
  • References in machine learning: works by Max Welling team, notably by Taco Cohen (from 2016), or e.g. [Geometric and physical quantities improve E(3) equivariant message passing; Johannes Brandstetter, et al, and Max Welling, ICLR 2022]

Learning the invariance

Choosing physically meaningful metrics

Optimal transport (Sinkhorn approximation)

• [Sinkhorn Distances: Lightspeed Computation of Optimal Transportation Distances; Marco Cuturi; NIPS 2013]
  and in primal form: [Learning Generative Models with Sinkhorn Divergences; Aude Genevay, Gabriel Peyré, Marco Cuturi; AISTATS 2018]
• Goal: to compare output distribution $p$ with desired (ground truth) one $q$
• Optimal transport: a distance between distributions, quantifying how much work is needed to transform one distribution into the other one. Analogy: moving earth with a shovel, minimizing the energy required, taking into account the mass and the distance to be transported.
  $\implies$ better distance than $L_2$ norm between distributions... or than $KL$ (the Kullback-Leibler divergence doesn't handle geometry: exact target bin, not around: no notion of neighborhood or distance between bins)
• Optimal transport formulation: $$\inf_{\text{transport fields} \;w\; \text{matching} \; p\; \text{and}\; q} \int_{x,y} w(x,y) C(x,y) dx dy $$ where $C(x,y)$ is the cost of moving some unit mass from point $x$ to point $y$,
  where $w(x,y)$ is the quantity of mass transported from point $x$ to point $y$,
  and where the conditions on the transport $w$ write:
  • reach the target distribution: $\forall y, \;\; \int_x w(x,y) dx = q(y)$
  • start from the candidate distribution: $\forall x,\;\; \int_y w(x,y) dx = p(x)$
    then return the total transportation cost
  
  
• Issue: closed form solution in 1D space, but too expensive to compute in higher dimensional space $\implies$ approximation schemes; in particular, approximation by Sinkhorn divergences
  • in both dual/primal formulations: if distributions are sets of points of identical masses (Dirac peaks), then solving the optimal transport problem is equivalent to searching for a bistochastic (*) transport matrix $W$ minimizing $W\,.*\;C$
    (*) bistochastic = all lines and rows sum up to 1
  • approximation: add a + $\epsi\, \text{entropy}(W)$ cost, making the problem convex (unique solution)
  • $W$ is necessarily of the form $\text{diag}(u) K \text{diag}(v)$, with $K = e^{-C/\epsi}$ and only one matrix satisfies this
  • Sinkhorn-Knopp algorithm [1967]: $W$ is obtainable by the iterative algorithm (proved to converge): $$u \;\; ./\!= \;\; K v$$ $$v \;\; ./\!= \;\; K u$$ starting from $u$ and $v = (1 1 1 1\dots)$ and at convergence return: $$u\; (K \; .* \; C) \; v$$ as $\sum_{ij} K_{ij} u_i v_j$ stands for $\int_{xy} w(x,y) dx dy$ and $C_{ij}$ stands for the transport cost $C(x,y)$.
  • this is implementable with a (fixed in advance) number of simple neural network layers, as all operations are differentiable
  
  
• thus the (approximated) optimal transport cost $\text{OT}(p,q)$ can be used in an optimization process such as backpropagation: $\displaystyle\;\; \min_f \sum_{\text{examples}\; k} \text{OT}( f(\text{ex}_k), \text{target} \; q_k$ ).

Minimum Mean Discrepancy

Metric learning: Siamese networks

• estimate the best metric (e.g. for some classification task), i.e. for instance, a mapping to another space, in which the Euclidean distance will be relevant
• if desired distances (between given points) or clusters are known, define a loss on triplets $(x,p,n)$, such as $$\sum_{(x,p,n)} max(0, d(x,p) - d(x,n) + m)$$ where
  • $x$ : current sample,
  • $p$ : positive example : $d(x,p)$ should be small
  • $n$ : negative example : $d(x,n)$ should be large
  • $m$ : arbitrary margin
  The optimization of such a loss will push together positive samples with $x$ and push away negative ones from $x$.
  NB : without margin and clamping, the optimization would provably diverge.
• named Siamese because the network $\varphi$ needs to be applied twice (to $x$ and $p$, e.g.) in order to be able to copmute the (Euclidean) distance in the output space (between $\varphi(x)$ and $\varphi(p)$).

Noisy data (can be seen as noise modeling)

Denoising auto-encoder

• originally meant to robustify auto-encoders (without requiring few middle neurons)
• get noisy inputs (in the article, artificial additional noise), ask for reconstruction without noise
• learns to get robust features and to denoise

What if noise is already present in the dataset, but unknown? (no denoised target available)

• data self-realignment : possible?
• example: registering RGB satellite images to cadaster maps (binary pictures indicating building presence): no exact ground truth available (spurious deformations in data acquisition & elevation landscape / human mistakes in making cadasters)
  • [Aligning and Updating Cadaster Maps with Aerial Images by Multi-Task, Multi-Resolution Deep Learning; Nicolas Girard, Guillaume Charpiat, Yuliya Tarabalka; ACCV 2018]
  • [Noisy Supervision For Correcting Misaligned Cadaster Maps Without Perfect Ground Truth Data; Nicolas Girard, Guillaume Charpiat, Yuliya Tarabalka; 2019]
    
    
    
• in the case of a regression task : $x \mapsto y$ with noisy dataset samples $(x,y)$ :
  • if output noise (on $y$) is ~i.i.d. (does not depend on x)
    or more exactly: if "relatively similar" $x, x'$ do not share more similar noise on $y, y'$
    then no bias in the dataset
  • if loss = $L_2$ metric : $\sum_i \| \hat{y}(x_i) - y_i \|^2$ with $y_i = y_i \;\text{real}$ + unknown $\text{noise}_i$
    then, with the following assumptions:
    • no noise bias (condition above on similar $x$)
    • no overfit
    • dense sampling limit (each sample has many neighbors)
    the optimal $\hat{y}(x_i)$ is reached at $y_i$ real!
  • in practice: denoise the dataset this way (here, re-align) and then re-learn from the aligned dataset (as less noise $\implies$ better results [theoretically same global optimum, but with different confiedences (= variance)])

Incorporating physical knowledge: Example of learning dynamics equations

Data assimilation

Learning a Partial Differential Equation (real equation not known)

• genetic optimization (of possible terms to incorporate in the equation)
• a PDE is an iterative process $\implies$ model it as a recurrent network
  • PDE = leaky RNN, i.e. not of the type $h_{t+1} = f\left(h_t\right)$ but of the form $h_{t+1} = h_t + f\left(h_t\right)$ : small iterative updates
  • example: segmentation refinement
    [Recurrent Neural Networks to Correct Satellite Image Classification Maps; Emmanuel Maggiori, Guillaume Charpiat, Yuliya Tarabalka and Pierre Alliez; Transactions on Geoscience and Remote Sensing 2016]
    In the spirit of image processing PDEs, learn an iterative process to deblur segmentation maps, using the original RGB image (whose edges might bring useful information)
    
    
• going further: not using a RNN, but using an Ordinary Differential Equation (ODE) solver $\newcommand{\dd}{\partial}$
  [Neural Ordinary Differential Equations; Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud; best paper at NeurIPS 2018]
  • given $f_\theta$, which describes the dynamics by $\frac{dh}{dt} = f_\theta\left(h_t\right)$, and given an initial condition $h_{t_0}$, use an ODE solver to compute $h_t$ at any real continuous time $t > t_0$
    $\implies$ more precise than a RNN with discretized time steps
  • the dynamics might depend also on $t$, using $\frac{dh}{dt} = f_{\theta, t} \left(h_t\right)$, for instance using a neural network $f_\theta$ with two inputs: $t$ and $h_t$
  • given a loss to be minimized $L(h_{T})$ with respect to the dynamics $f_{\theta,t}$, one can similarly use an ODE solver to compute $\nabla_\theta L(h_T)$:
    • define the "adjoint" $a(t) = \frac{\dd L}{\dd h_t}$, which tells how the state $h_t$ should change at time $t$ to decrease the loss
    • using the chain rule (as for backpropagation), this adjoint satisfies: $$\frac{d a(t)}{dt} = - a(t)^\top \, \frac{\dd f_{\theta,t}( h_t )}{\dd h_t} $$
    • and then the total variation with respect to the parameters $\theta$ can be expressed by integration: $$\frac{dL}{d\theta} = - \int_{t_1}^{t_0} a(t)^\top\,\frac{\dd f_{\theta,t}( h_t )}{\dd\theta}\,dt$$
    • this integral can be computed using an ODE solver...
  • thus one can learn the dynamics $f_{\theta,t}$
  • example: complete a temporal series $(x_0, x_1, x_2 \dots x_N)$:
    • consider that the dynamics learned / to be learned do not act directly on $x_t$ but on an internal state $h_t$ (in order to be able to deal with partial or noisy information, etc.)
    • so first, transform this sequence into a guessed initial internal state $\hat{h}_{t=0}$ (named $z_0$ in the figure below), using an RNN (going reverse in time, from $x_N$ to $x_0$; the RNN has to be learned as well)
    • then apply the dynamics $f_{\theta,t}$ previously learned, to $\hat{h}_0$ (using an ODE solver)
    • this gives guessed states $\hat{h}_t$ for all times, in particular $\hat{h}_{t>N}$
    • from them, deduce missing observations $\hat{x}_{t>N}$
    
    
  
  
• choosing relevant sensors and mixing information
  • example of hurricane trajectory forecast, from 30 possible sensors of various dimensions and units (temperature, pressure, wind field, ...) [Deep Learning for Hurricane Track Forecasting from Aligned Spatio-temporal Climate Datasets; Sophie Giffard-Roisin, Mo Yang, Guillaume Charpiat, Balázs Kégl and Claire Monteleoni; Modeling and decision-making in the spatiotemporal domain workhop at NIPS 2018]
  • choose a few relevant sensors only, thanks to a sparse feature selection technique (e.g., Automatic Relevance Determination, based on linear regression)
  • notice possible optimization issues when fusing all information sources into one input only (different learning rates might be needed for each sensor)
  • so, build and train independently one sub-network per sensor
  • and merge their last layers (re-train to fine-tune)
  • time incorporated as a convolution (but could be as an LSTM e.g.)
    

Incorporating invariances/symmetries of the problem

• eg: translation / rotation / permutation... or symmetry between variables (shared blocks of networks)

Knowing an equation that the solution has to satisfy : solving PDEs!

• equation to solve, of the form:

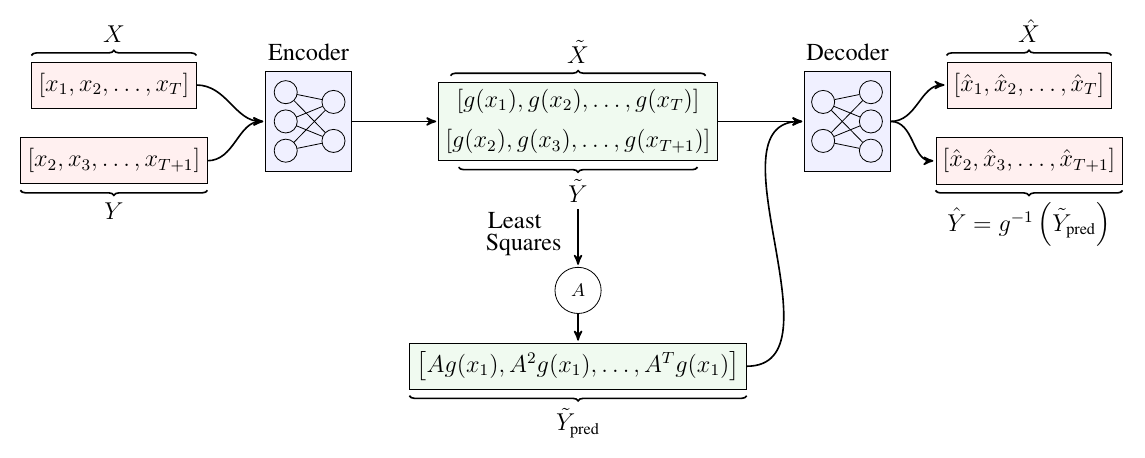
  	$\dd_t\, u(t,x) + L\, u(t,x) = 0 \;\;\;\; \forall t, x \in [0,T]\times\Omega$
  with constraints	$u(0,x) = u_0(x) \;\;\;\; \forall x \in \Omega\;\;\;$	[initial condition]
  and	$u(t,x) = g(t,x) \;\;\;\; \forall x \in [0,T] \times \dd\Omega\;\;\;$	[boundary condition: control]

  
  where:
  • one searches for a function $u$ defined over a spatio-temporal domain $\Omega\times[0,T]$
  • $L$ is a differential operator, not necessarily linear, applied to function $u$
  • $\dd_x$ denotes the partial derivative with respect to $x$
  • $\dd\Omega$ denotes the boundary of domain $\Omega$
  
  
• minimize $J(f) = \| \dd_t f + L f\|^2_{[0,T]\times\Omega} + \|f-g\|^2_{[0,T]\times\dd\Omega} + \|f(0,.) - u_0\|^2_\Omega$
• operators such as $\dd_t$ or $L$ are easy to implement on top of the network providing $f$
• proved (under assumptions) and checked experimentally to converge to 0 (and $f \to $ solutions)
• in practice: replace integral with Monte Carlo estimates (i.e. $\E_{\text{batch samples}}$ ...) and replace second-order derivatives $\dd_{x_1} \dd_{x_2} f(t,x)$ with approximations of type $\frac{ \dd_x f(t,x+\epsi) - \dd_x f(t,x) }{\epsi}$.

Important example in chemistry

• Finding or approximating quantum mechanics equations' solutions is a very important topic in chemistry, as these equations are hard to solve (very heavy computations) and molecule properties depend on them
• (energy) potential function $U(x)$ around a molecule $x$: hard to model / compute
• with ML : train $x \mapsto U(x)$ from simulations
• desired physical property: $- \dd_x U(x) = \text{ForceField}(x)$
• minimize $\| \dd_x U(x, \theta) + \text{ForceField}(x)\|^2$ w.r.t. $\theta$ (parameters of the neural network standing for $U$)

Form of the solution known

• goal: prediction of the evolution of temperature maps (sea surface temperature, from satellite imagery)
• equation satisfied by the fluid (the ocean streams): advection-diffusion: $$\dd_t I + w \cdot \dd_x I = D\, \dd^2_{xx} I$$ ($\dd^2_{xx}$ = Laplacian, $D$ = diffusion constant, $w$ = unknown motion field)
• theorem: the solution of this equation is of the form: $$I(x,t) = \int_{\R^2} \frac{1}{4\pi D\,t} e^{- \frac{\|x-y-w\|^2 }{4Dt}} I_0(y) dy$$
• instead of predicting directly the new state at $t+1$ by learning $I(.,t) \mapsto I(.,t+1)$ directly, learn to predict the motion: $I(.,t) \mapsto w(.,t)$ from which one can estimate $I(.,t+1)$
• criterion to optimize: good prediction of $I(t+1)$ + regularization of $w$ (smooth, small, small divergence)
       
  $\implies$ better results than direct prediction; this said, the same team, in a later paper, without using the solution form, but using an ODE solver, obtained better results [Learning Dynamical Systems from Partial Observations; Ibrahim Ayed, Emmanuel de Bézenac, Arthur Pajot, Julien Brajard, Patrick Gallinari; 2019]

In practice

Deep for physic dynamics : learning and controlling the dynamics

• $x_{t+1} = F(x_t)$ with fixed, unknown function $F$, and $x_t \in \R^d$
• if $F$ is linear: "easy" (or, at least, a classic problem) to retrieve from data samples $(x_t, x_{t+1}, \dots)$ as a mean square problem $\displaystyle \sum_{\text{samples} \; x} \|x_{t+1} - A\, x_t\|^2$
• solution: note $X = [x_1, x_2, ... x_T]$
  and $Y = [x_2, x_3, ... x_{T+1}]$
  then the matrix $Y\, X^\dagger \to$ optimal $A$ when $T$ increases
  where $X^{\dagger}$ is the Moore-Penrose pseudo-inverse of $X$, which is $\displaystyle \;\;\lim_{\epsi\to 0}\;\; (X^* X + \epsi\, \mathrm{Id})^{-1} X$
• what if $F$ non linear?

• Theorem: there exists a representation space in which any dynamical system becomes linear
  $\implies$ approximate this representation with a neural network! and learn linear dynamics there
• unfortunately: this representation space = a complex Hilbert space (i.e., infinite-dimensioned vector space)

• train a network $g:$

  $X \to X'$

  $Y \to Y'$

  mapping to another space,
  such that the dynamics in that space are linear, i.e. $Y' = A' X'$ for some matrix $A'$
  and the inverse network $h = g^{-1} :$

  $ X' \to X$

  $Y' \to Y$

  .
  Then, for new $X$, predict $h\big( A'( g(X) ) \big)$ [supposed to be close to $Y$]
  
  
• loss: $\|X - h(g(X))\|^2$ : reconstruction error of the auto-encoder $h \circ g$
  $+\; \|Y - h(A'(g(X)))\|^2$ : prediction error
• NB: given $X'$ and $Y'$, the optimal matrix $A'$ (best linear dynamical model) can be computed in closed form as above for the linear case. The non-linearity of the dynamics in that space can be measured by how much $A'X'$ differs from $Y'$ for that best $A'$.
• idem for control

• [Koopman Theory for Partial Differential Equations; J. N. Kutz, J. L. Proctor, and S. L. Brunton; Complexity, 2018]
• [Deep learning for universal linear embeddings of nonlinear dynamics; B. Lusch, J. N. Kutz, S. L. Brunton; Nature Communications 2018]