Résumé de l'épisode précédent

On a fait une seconde série de rappels sur la langage OCaml

• Le polymorphisme : avoir des types avec des variables ('a, 'b, …)
  ex: fst: 'a * 'b -> 'a
• Le type des listes 'a: un type somme prédéfini en OCaml représentant une suite de valeurs d'un type 'a
  • Listes littérales [1; 2; 3; 4]
  • Construction x::l
  • Filtrage : match l with [] -> (* cas de la liste vide *) | x :: ll -> (* cas d'une liste formée d'un premier élément x et une suite ll *)
  • Le module List et ses fonctions, en particulier des itérateurs (List.map f l, …)
• Les fonctions récursives et en particulier la récursion terminale

Motivations

La structure de liste ne permet pas de représenter efficacement des ensembles

• Maintenir des éléments ordonnés (insertion en O(n))
• Rechercher un élément (le plus petit O(1), le plus grand, O(n))
• Union/Intersection/Différence : O(n+m)

La structure d'ensemble ordonnée est très importante en informatique

• Création de collection sans doublon
• Recherche efficace d'éléments
• Implémentation de dictionnaires

Quelle autre structure utiliser

Arbre Binaire de Recherche (ABR)

Un arbre binaire de recherche est un arbre binaire stockant des valeurs aux nœuds internes avec la propriété suivante:

Pour tout nœud interne, la valeur du nœud est supérieure aux valeurs du sous-arbre gauche et inférieure aux valeurs du sous-arbre droit.

Note: un arbre binaire est un arbre ordonné (l'ordre des enfants d'un nœud est significatif) dont les nœuds internes ont exactement 2 enfants.

Représentation en OCaml

Un ABR peut être représenté par le type OCaml

type 'a tree = Leaf | Node of ('a tree * 'a * 'a tree)

Il représente soit une feuille, soit nœud interne contenant une valeur de type 'a et 2 sous-arbres.

Hypothèse : on suppose l'existence d'une fonction:

val compare :'a -> 'a -> int

Cette fonction peut comparer deux valeurs x et y d'un même type et renvoie :

• Un entier négatif si x < y
• 0 si x = y
• Un entier positif si x > y

Pour l'instant on suppose qu'elle calcule la comparaison « naturelle » (sur les entiers, les chaînes de caractères, …). On reviendra dans un autre cours sur cette hypothèse.

Exemple

L'arbre :

Est représenté par :

let t_ex = Node (Node (Node (Leaf, 0, Leaf), 4, Node (Node (Leaf, 5, Leaf), 6, Node(Leaf, 7, Leaf))), 8, Node (Leaf, 12, Node (Node (Leaf, 13, Leaf), 14, Leaf)))

∈ (appartenance)

Une opération basique est de savoir si une valeur v est dans un arbre t:

let rec mem v t = match t with | Leaf -> false | Node (_, l, w, r) -> let c = compare v w in if c = 0 then true else if c < 0 then mem v l else mem v r

La fonction est-elle récursive terminale ? oui !

Illustration

On recherche 5 dans l'arbre :

Complexité de la recherche ?

La complexité de la recherche est bornée par la hauteur de l'arbre.

Ce qui nous intéresse est la complexité par rapport au nombre d'éléments. Elle dépend de la forme de l'arbre :

2h - 1 nœuds, hauteur logarithmique		h nœuds, hauteur linéaire

Qu'est-ce qui peut causer ces situations ?

Ajout naïf

let rec naive_add v t = match t with | Leaf -> Node (Leaf, v, Leaf) | Node (l, w, r) -> let c = compare v w in if c = 0 then t else if c < 0 then Node (naive_add v l, w, r) else Node (l, w, naive_add v r)

• Ajout 5, 3, 8, 1, 4, 7, 10 (dans cet ordre) ⇒
• Ajout 1, 3, 4, 5, 7, 8, 10 (dans cet ordre) ⇒

Comment faire ?

On souhaite ré-équilibrer l'arbre progressivement :

	⮏
déséquilibre détecté		réparation

On veut détecter cette situation pour des sous-arbres arbitrairement grands.

On doit donc:

• Garder de l'information supplémentaire dans les nœuds
• L'utiliser pour ré-équilibrer l'arbre lors d'opérations élémentaires
• Exprimer toutes les opérations en termes d'opérations élémentaires

Arbres binaires annotés

type ('a, 'info) tree = | Leaf | Node of ('info * ('a, 'info) tree * 'a * ('a, 'info) tree)

On modifie le type des arbres pour prendre 2 paramètres

• Le paramètre 'a ne change pas, il indique le type des éléments
• Le paramètre 'info représente une information supplémentaire qui sera utilisée pour ré-équilibrer l'arbre

Il y a plusieurs sortes d'informations que l'on peut stocker, en fonction des différents arbres binaires de la littérature: arbres AVL, arbres rouges-noirs, arbres à poids équilibrés, treap, …

Nous verrons pour certains d'entre eux les détails du ré-équilibrage.

Itérateurs

Les itérateurs doivent (par définition) parcourir toutes les valeurs de la collection une à une ⇒ au mieux O(n).

La complexité ne dépend pas de la forme de l'arbre.

let rec iter f t = match t with | Leaf -> () | Node (_, l, v, r) -> iter f l; (* parcours sous-arbre gauche *) f v; (* puis nœud courant *) iter f r (* puis sous-arbre droit *) let pr_int_tree t = iter (fun i -> Printf.printf "%d " i) t let () = pr_int_tree t_ex (* exemple du slide t *) (* affiche 0 4 5 6 7 8 12 13 14 *)

Fold

L'itérateur fold permet de calculer une opération d'agrégat sur les valeurs stockées dans l'arbre

let rec fold f t acc = match t with | Leaf -> acc | Node (_, l, v, r) -> let acc_l = fold f l acc in let acc_v = f v acc_l in fold f r acc_v let size t = fold (fun _ acc -> 1 + acc) t 0 let sum_int_tree t = fold (fun x acc -> x + acc) t 0 let prod_float_tree t = fold (fun x acc -> x *. acc) t 1.0 let to_list_rev t = fold (fun x acc -> x :: acc) t [] let l = to_list_rev t_ex (* l = [ 14; 13; 12; 8; 7; 6; 5; 4; 0 ] *)

Valeur minimale/maximale

On peut implémenter le min avec fold :

let min_opt x y = match (x, y) with | None, _ -> y | _, None -> x | Some xx, Some yy -> (* fonction min d'OCaml qui utilise compare *) Some (min xx yy) let naive_min_tree_opt t = fold min_opt t None let n = naive_min_tree_opt t_ex (* renvoie Some 0 *)

🤔 : est-ce vraiment raisonnable ?

Complexité linéaire, on peut faire mieux.

Valeur minimale/maximale

let rec min_elt_opt t = match t with | Leaf -> None (* arbre vide *) | Node (_, Leaf, v, _) -> Some v (* valeur la plus à gauche *) | Node (_, l, _, _) -> min_elt_opt l

Complexité : hauteur de l'arbre

Remarque : on renvoie une option pour avoir quelque chose à renvoyer dans le cas de l'arbre vide.
Une définition alternative lève une exception dans le cas vide et renvoie directement la valeur.

let rec min_elt t = match t with | Leaf -> failwith "arbre vide" (* lève une exception *) | Node (_, Leaf, v, _) -> v | Node (_, l, _, _) -> min_elt_opt l

Valeur maximale : symétrique, on renvoie la valeur la plus à droite.

Autres itérateurs

forall, exists :

let rec exists p t = match t with | Leaf -> false | Node (_, l, v, r) -> exists p l || p v || exists p r let forall p t = not (exists (fun v -> not (p v)) t)

La fonction exists explore-t'elle tout le temps tout l'arbre ?

⇒ non car l'opérateur || est paresseux:

(* équivalent à *) | Node (_, l, v, r) -> let c = exists p l in if c then true (* on s'arrête si vérifié dans l'arbre gauche *) else let c = p v in if c then true (* on s'arrête si vérifié dans le nœud *) else exists p r (* sinon on cherche dans l'arbre droit *)

map ?

Attention, la version naïve est incorrecte:

let rec wrong_map f t = match t with | Leaf -> Leaf | Node (i, l, v, r) -> Node (i, wrong_map f l, f v, wrong_map f r)

😱 : la fonction f ne préserve pas l'ordre (a priori)

Si on suppose qu'on a une fonction

val add : 'a -> ('a,'info) tree -> ('a,'info) tree

qui ajoute un élément (correctement) dans l'arbre alors

let map f t = fold (fun x acc -> add (f x) acc) t Leaf

Complexité : n opérations add (attention add n'est a priori pas en temps constant).

Quelles opérations

On n'a pas encore vu comment construire un ABR équilibré, ni comment maintenir l'équilibre.

• Les opérations qui construisent un arbre on l'air dépendante de la stratégie (en part. des informations stockées)
• On aimerait cependant éviter de ré-écrire toutes les fonctions ensemblistes pour chaque type d'ABR.

⇒ on présente une méthode générique, qu'on appliquera à au moins 3 types d'arbres différents (AVL, arbres rouges-noirs, arbres à poids équilibrés)

⇒ cette méthode donne la complexité optimale pour la structure d'ABR pour les opérations que l'on va définir.

Quelles opérations (2)

On souhaite définir les opérations ensemblistes suivantes

• val union : ('a, 'info) tree -> ('a, 'info) tree ->('a, 'info) tree
• val inter : ('a, 'info) tree -> ('a, 'info) tree ->('a, 'info) tree
• val diff : ('a, 'info) tree -> ('a, 'info) tree ->('a, 'info) tree

Remarque : si union a une complexité optimale, alors on peut définir add:

let add v t = union t (Node(Leaf, v, Leaf)) (* on fait l'union de t et de l'arbre représentant l'ensemble singleton { v } *)

On va supposer l'existence d'une opération élémentaire qui va nous permettre d'exprimer toutes les autres.

join

On suppose l'existence d'une fonction join :

val join : ('a, 'info) tree -> 'a -> ('a, 'info) tree -> ('a, 'info) tree

Telle que : join l v r renvoie la valeur de l'arbre formé par l, v et r et correctement ré-équilibré, en faisant l'hypothèse que toutes les valeurs de l sont plus petite que v et toutes les valeurs de r sont plus grandes que v.

En particulier, l et r peuvent être de forme quelconque, join s'occupe de ré-équilibrer l'arbre final.

En quoi ça nous aide ?

Opérations dérivées de join (1) : split

let rec split join t v = match t with | Leaf -> (Leaf, false, Leaf) | Node (i, l, w, r) -> let c = compare v w in if c = 0 then (l, true, r) else if c < 0 then let ll, b, lr = split join l v in (ll, b, join lr w r) else let rl, b, rr = split join r v in (join l w rl, b, rr)

• split t v prend un arbre t et une valeur v et renvoie un triplet l, b, r où l (resp. r) est l'arbre de toutes les valeurs plus petites (resp. plus grandes) que v, et b vaut true ssi v est dans t
• join est prise en argument car on ne connaît pas encore son code

Autrement dit, split t v partage t en deux arbres selon la valeur pivot v.

Opérations dérivées de join (2) : remove_max_elt

let rec remove_max_elt join t = match t with | Leaf -> failwith "arbre vide" | Node (_, l, v, Leaf) -> (l, v) | Node (_, l, v, r) -> let rr, w = remove_max_elt join r in (join l v rr, w)

• remove_max_elt t renvoie le plus grand élément de t et l'arbre privé de cet élément
• Suppose que tn'est pas vide
• join est prise en argument car on ne connaît pas encore son code

Opérations dérivées de join (3) : merge

let rec merge join l r = match l with | Leaf -> r | _ -> let ll, v = remove_max_elt l in join ll v r

• merge l r fusionne deux arbres l et r
• Suppose que toutes les valeurs de l sont inférieures aux valeurs de r
• join est prise en argument car on ne connaît pas encore son code

Alors avec ça on fait quoi ?

add

let rec add join v t = let l, b, r = split join t v in if b then t else join l v r

• add v t ajoute v à t
• Garde l'arbre initial si v est dans t
• Est optimale si join est optimal (car split dépend de join)
• join est prise en argument car on ne connaît pas encore son code

remove

let rec remove join v t = let l, b, r = split join t v in if b then merge l r else t

• remove v t supprime v à t
• Garde l'arbre initial si v n'est pas dans t
• Est optimale si join est optimal (car split dépend de join)
• join est prise en argument car on ne connaît pas encore son code

union

let rec union join t1 t2 = match (t1, t2) with | Leaf, _ -> t2 | _, Leaf -> t1 | _, Node (_, l2, v2, r2) -> let l1, _, r1 = split join t1 v2 in let ll = union join l1 l2 in (* union des plus petits que v2 *) let rr = union join r1 r2 in (* union des plus grands que v2 *) join ll v2 rr (* on reconstruit l'arbre *)

• union t1 t2 renvoie l'union de t1 et t2
• Est optimale si join est optimal (preuve compliquée)
• join est prise en argument car on ne connaît pas encore son code

inter

let rec inter join t1 t2 = match (t1, t2) with | Leaf, _ | _, Leaf -> Leaf | _, Node (_, l2, v2, r2) -> let l1, _, r1 = split join t1 v2 in let ll = inter join l1 l2 in (* inter des plus petits que v2 *) let rr = inter join r1 r2 in (* inter des plus grands que v2 *) if b then (* v2 était aussi dans t1 *) join ll v2 rr else (* v2 pas dans t1, il n'est pas dans l'intersection *) merge ll rr

• intersection t1 t2 renvoie l'intersection de t1 et t2
• Est optimale si join est optimal (preuve compliquée)
• join est prise en argument car on ne connaît pas encore son code

diff

let rec diff join t1 t2 = match (t1, t2) with | Leaf, _ -> Leaf | _, Leaf -> t1 | _, Node (_, l2, v2, r2) -> let l1, _, r1 = split join t1 v2 in let ll = diff join l1 l2 in (* retire de l1 les plus petits que v2 *) let rr = diff join r1 r2 in (* retire de r1 le plus grand que v2*) merge join ll rr (* fusionne sans remettre v2 *)

• intersection t1 t2 renvoie l'intersection de t1 et t2
• Est optimale si join est optimal (preuve compliquée)
• join est prise en argument car on ne connaît pas encore son code

Plusieurs stratégies ?

Il existe dans la littérature plusieurs types d'ABR. Ils ont été découverts indépendamment il y à longtemps, mais le fait qu'ils sont exprimables uniquement avec join dans un cadre fonctionnel est récent (1993, Adams, Efficient sets--a balancing act, JFP) et la preuve d'optimalité est plus récente encore (2016, Just Join for Parallel Ordered Sets, Belloch, Ferizovic, Sun, SPAA'16).

Parmi les stratégies possibles

• Arbres AVL: l'information gardée est la hauteur de l'arbre (int)
• Arbres Rouges-Noirs : l'information gardée est la couleur du nœud (type color = Red | Black)
• Arbres à poids équilibrés (Weight Balanced binary trees) : l'information gardée est la taille de l'arbre (int)

AVL

• Plus ancienne structure connue d'ABR équilibré
• découverte en 1962 par Georgy Adelson-Velsky et Evgenii Landis (URSS)

Principe : on conserve la hauteur de l'arbre dans le nœud. One ré-équilibre les arbres dès que le la hauteur de 2 sous-arbres diffère de plus de 1.

Types et opérations de base

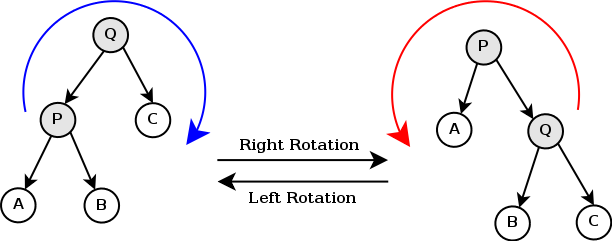
type 'a avl = ('a, int) tree (* équivalent à : type 'a avl = Leaf | Node of (int * 'a tree * 'a * 'a tree) *) let height t = match t with Leaf -> 0 | Node (h, _, _, _) -> h let empty = Leaf let node l v r = let hl = height l in let hr = height r in Node (1 + max hl hr, l, v, r) let rotate_left t = match t with | Node (_, l, v, Node (_, lr, vr, rr)) -> node (node l v lr) vr rr | _ -> failwith "erreur rotate_left" let rotate_right t = (* code symétrique *) match t with | Node (_, Node (_, ll, vl, rl), v, r) -> node ll vl (node rl v r) | _ -> failwith "erreur rotate_right"

Types et opérations de base

• On stocke la hauteur dans l'arbre
• La fonction height permet de renvoyer la hauteur
• La fonction node permet de construire un nœud en calculant la nouvelle hauteur
• Les fonctions de rotation (gauche ou droite) sont les primitives pour ré-équilibrer :

join_avl_right

(* suppose que l est trop grand par rapport à r ⇒ hauteurs diffèrent de plus que 1 *) let join_avl_right l v r = match l with | Leaf -> failwith "impossible" | Node (_, ll, vl, rl) -> if height rl <= height r + 1 then let new_r = node rl v r in if height ll <= height new_r + 1 then node ll vl new_r else rotate_left (node ll vl (rotate_right new_r)) else let new_r = node rl v r in let new_t = node ll vl new_r in if height new_r <= height ll + 1 then new_t else rotate_left new_t let join_avl_left l v r = (* symétrique *)

join_avl

let join_avl l v r = if height l > height r + 1 then join_avl_right l v r else if height r > height l + 1 then join_avl_left l v r else node l v r let add_avl v t = add join_avl v t let remove_avl v t = remove join_avl v t let union_val t1 t2 = union join_avl t1 t2 let inter_val t1 t2 = inter join_avl t1 t2 let diff_val t1 t2 = diff join_avl t1 t2

Toute la difficulté du code est concentrée dans 1 fonction (et son symétrique).

Le but du TP sera de comprendre en détail ce qui se passe lors de la rotation (graphiquement).

La semaine prochaine : d'autres types d'arbres (donc d'autres fonctions join) et des considérations sur l'occupation mémoire.