Multi-Layer Perceptron {0;1}

Introduction

A multi-layer perceptron is made up of several layers of neurons. Each layer is fully connected to the next one. Moreover, each neuron receives an additional bias input as shown in figure 1:

I^p 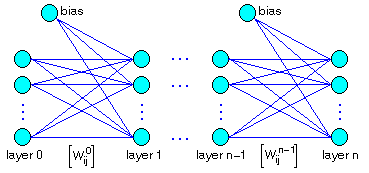A^p

• W_ij^k = weight from unit i (in layer v) to unit j (in layer v+1).
• I^p = input vector (pattern p) = (I₁^p, I₂^p, ..., I_b^p).
• A^p = Actual output vector (pattern p) = (A₁^p, A₂^p, ..., A_c^p).

In this applet, the ouput values of the neurons stand in {0;1}.

Credits

The original applet was written by Olivier Michel.

Instructions

To change the structure of the multi-layer perceptron:

1. change the values H1, H2 and H3 corresponding to the number of units in the first second and third hidden layer. If H3 is equal to 0, then only two hidden layers are created ; if both H3 and H2 are equal to 0 a single hidden layer is created and if all H1, H2 and H3 are null, no hidden layer is created, corresponding to a single layer perceptron.
2. click on the Init button to build the requested structure and initialize the weights.

Applet

Questions

1. Try to characterize the problems the simplest multi-layer perceptron is able to solve. Reminder: the  simplest multi-layer perceptron would be a multi-layer perceptron with a single hidden layer containing a single unit. Is it able to solve  classification problems which are not linearly separable?
2. Set three clusters of points in a line: a red one with 3 points, a blue one with 6 points, then a red one with three points. Does the simplest multi-layer perceptron solve this problem ? If not, what is the minimuls structure necessary to solve the problem? With which momentum and learning rate ?
3. Set a cluster of red points (1.0) in the center, surrounded by blue points. Which network structure and which momentum / learning rate combination can solve such a problem?