Uniformly random colourings of sparse graphs
Eoin Hurley and François Pirot.
Uniformly Random Colourings of Sparse Graphs.
In STOC ’23: 55th Annual ACM Symposium on Theory of Computing, pages 1357–1370, Orlando FL USA, France, June 2023. ACM.
DOI: 10.1145/3564246.3585242
HAL: hal-04245446
Context
This work was made possible by taking full advantage of a new technique often referred to as the Rosenfeld Counting Method which seems to improve on existing probabilistic methods such as Entropy Compression, with additional degrees of freedom that let us study many properties of graph colourings (among other combinatorial objects), and led to profound scientific advances. This is the topic of an ANR JCJC proposal involving François Pirot. This method has been explored by various members of the team (François Pirot, Quentin Chuet, Johanne Cohen).
Contribution
In this work, we study the reconfiguration properties of a uniformly random proper colouring of any given sparse graph right above the phase transition. This extends and improves previously known results that held only with high probability in a random graph of given average degree. This technique can be seen as a quantitative version of Entropy Compression, from which we could derive information about the expectation of a crucial quantity --- informally speaking, this corresponds to the degrees of freedom one has when incrementing the size of a partial solution. On top of that, we were able to prove large deviation inequalities in an unusual setting --- we have basically no control over the dependencies between the random events that we study --- and conclude that this quantity is highly concentrated above a sufficiently large threshold for our purpose.
Illustration
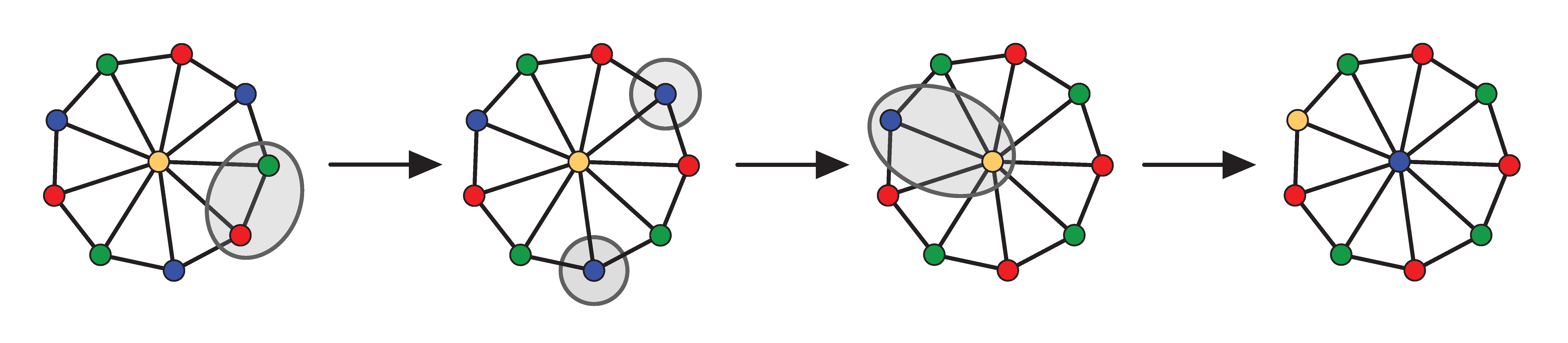
A recolouring process to change the colour of the middle vertex of a wheel. Only 4 colours are allowed, and one can recolour at most 2 vertices at each step.
Impact
This work has been accepted at STOC, one of the most selective theoretical computer science conferences on the other side of the Atlantic. François Pirot was invited to present this work in a plenary lecture at the annual meeting of the CoA (Complexity and Algorithms) working group of the GDR-IM (now GDR-IFM) in 2023.
Neural representation and learning of hierarchical 2-additive Choquet integrals
Romain Bresson, Johanne Cohen, Eyke Hüllermeier, Christophe Labreuche, and Michèle Sebag (A&O).
Neural Representation and Learning of Hierarchical 2-additive Choquet Integrals.
In IJCAI-PRICAI-20 - Twenty-Ninth International Joint Conference on Artificial Intelligence and Seventeenth Pacific Rim International Conference on Artificial Intelligence, pages 1984–1991, Yokohama, France, July 2020. International Joint Conferences on Artificial Intelligence Organization.
DOI: 10.24963/ijcai.2020/275
HAL: hal-03017078
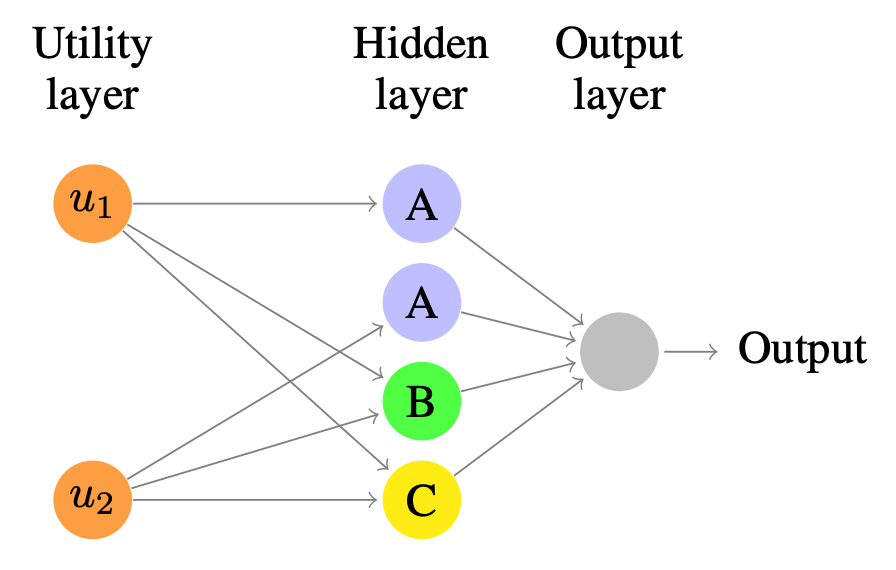
Context
Multi-criteria decision-making (MCDM) involves modelling expert preferences and assisting decision-makers in selecting options based on several criteria.
Contribution
We use the widely used MCDM model, the Choquet integral, and propose a machine learning-based approach that constructs a hierarchical model of Choquet integrals by aggregating criteria at multiple levels. Starting from models that assign a score with a given alternative, the aim is to solve three key problems: choice (identifying the best alternative), ranking (ordering the alternatives) and classification (giving each alternative a satisfaction class). The work involves adapting the Choquet integral and employing supervised learning techniques on data to develop such models and specifically to harness available data to learn the parameters of a multi-criteria decision support model. We explore the application of the Choquet integral, particularly hierarchical Choquet integrals that involve intermediate aggregations of interacting criteria.
Our primary contribution lies in the development of a learning-based method for automatically identifying hierarchical MCDA models, which consist of aggregators of Choquet integrals and utility functions. To achieve this, we propose a neural network architecture, referred to as Neur-HCI, that facilitates end-to-end learning of the model based on data reflecting expert preferences. The empirical validation of our approach on both real-world and artificial benchmarks demonstrates its effectiveness, showcasing favorable comparisons with state-of-the-art baseline methods.
Impact
This work was a part of Roman Bresson's CIFRE thesis, who obtained in 2022 the Thalès PhD. prize. This was also our first collaboration with the A&O team. A patent is being submitted.
The aperiodic Domino problem in higher dimension
Benjamin Hellouin de Menibus and Antonin Callard.
The aperiodic Domino problem in higher dimension.
In S. Dagstuhl, editor, 39th International Symposium on Theoretical Aspects of Computer Science (STACS 2022), number 18, pages 1–15, Marseille, France, Mars 2022.
DOI: 10.4230/LIPIcs.STACS.2022.18
HAL: hal-03573476
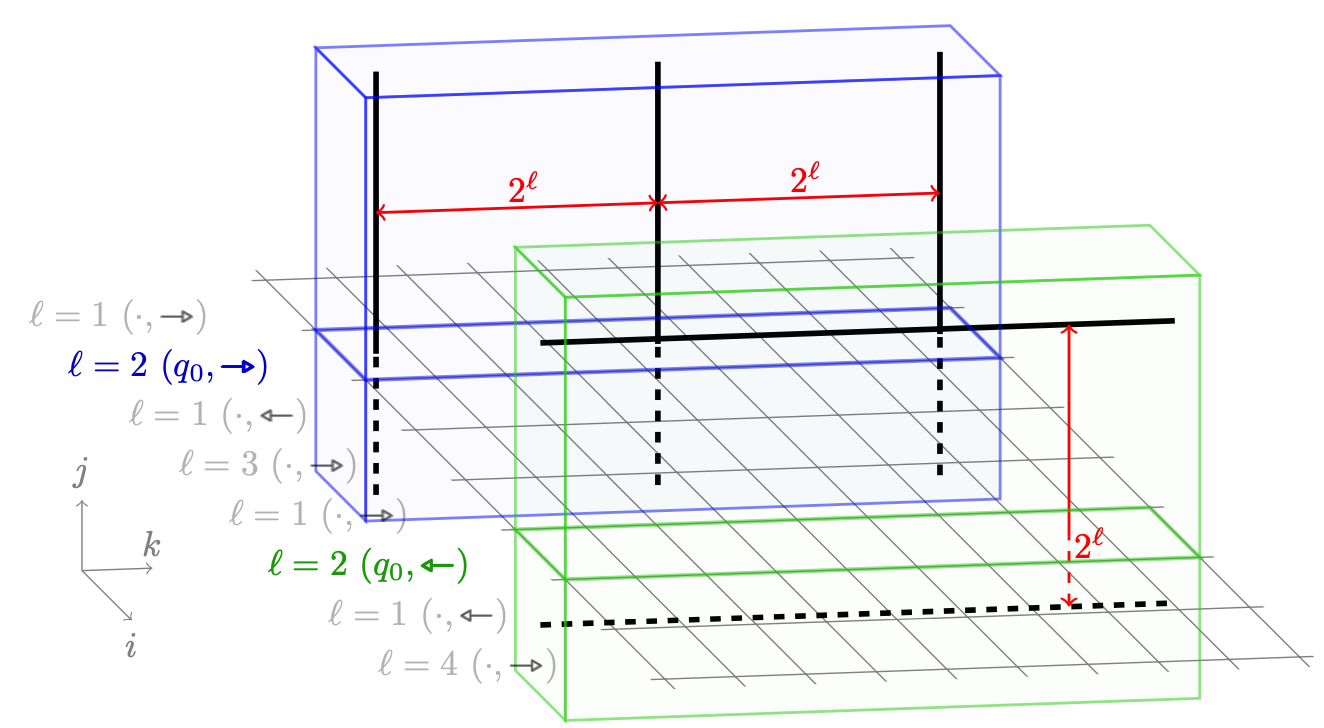
Context
A main axis in symbolic dynamics relates the the frontier of undecidability: the conditions under which some simple problems become decidable or undecidable. In the theory of tilings, the Domino problem is the single most studied problem (on the computer science side), while aperiodicity phenomena and quasiperiodic structures have been main motivations for the activity in the topic, motivated by various applications such as quasicrystals.
Contribution
We find and prove a qualitative difference in the structure of breaks of periodicity in tiling spaces between dimensions 2 and 4, which induces a jump in the computational difficulty of a variation of the classical Domino problem. This is the first time that such a jump is observed in higher dimension, with complex combinatorial and geometrical reasons underlying this phenomenon (complex enough that the 3-dimensional case remains open). Understanding the role of aperiodicity on computational and dynamical properties of the system is of interest not only for computer scientists, but for mathematician and statistical physisicists as well.
Impact
Antonin Callard was an M2 intern in the team. The article was accepted to STACS, one of the top European non-specialised conferences in theoretical computer science.
Les étoiles de l'Europe -- H2020 project OpenDreamKit
Trophy "Les étoiles de l'Europe" for the H2020 European Research Infrastructure project OpenDreamKit.

Context
From 2015 to 2019, Nicolas Thiéry coordinated the 7.6M€ Horizon 2020 European Research Infrastructure project (#676541) OpenDreamKit. Bringing together a diverse team of 50 Open Science enthusiasts across 17 sites all over Europe, including an average of 11 full time Research Software Engineers, it supported the joint ecosystems of software for mathematics and Jupyter, as a toolkit from which to build Virtual Research Environments.
Contribution
Beyond the coordination of the project, the team was heavily involved in all its work packages, from community building to scientific developments (e.g. around formalizing computational math software or HPC for combinatorics) to tackling, thanks to the recruitement of Research Software Engineers, long standing highly technical tasks, like porting SageMath and dependencies (several millions lines of code) to Windows, or helping migrating SageMath to Python 3.
The project also contributed to foster the Research Software Enginner movement.
Impact
OpenDreamKit was one of the twelve H2020 projects that were awarded the 2020 French CNRS trophy “Les étoiles de l’Europe” for their success and impact. The jury particularly appreciated the massive dissemination activities (110 events!) led by Viviane Pons, and the dedication to all aspects of Open Science: open source, open data, open publications and, special innovation of OpenDreamKit, open project setup and management.
More generally this award, together with other marks – 69 citations of the book "Computational Mathematics with SageMath" since 2019; 80 citations of the paper "Using Jupyter for Reproducible Scientific Workflows" since 2021; two SageMath Development Prizes; a Distinguished Jupyter Contributor award, many invitations –, exemplifies the impact of the heavy involvement of the team in the advocacy, community building, design and development of libre software and infrastructure for research and teaching, with important contributions to SageMath, Coq - Mathematical Component, or the Jupyter ecosystem.
Musical juggling, Automata and Combinatorics
Since 2016, Florent Hivert and Nicolas Thiéry are collaborating with the artist Vincent de Lavenère, juggler-author of the "Compagnie Chant de Balles", around the design of notations for writing musical juggling scores.

Context
Vincent de Lavenère has invented a new juggling prop, namely a ball containing a tuned bell which plays a specific note when catched. He is currently trying to create a "concerto for four jugglers and orchestra" composed by Vincent Bouchot. The difficulty is that the juggler acts when he throws the ball in the air but the note is played when he catches the ball.
Contribution
To produce a specific melody, one needs to carefully schedule in which order, when and at which height to throw the balls. This video presents the scientific question.
This combinatorial work led to the creation of a one-hour conference/show with a scientist and the artist, using musical juggling to introduce scientific concepts such as models and automata, funded by Fondation Blaise-Pascal, Institut Hadamard and La Diagonale Paris-Saclay.
New research questions raised by this collaboration (How to compute the juggling figure to play, e.g. "The blue Danube" ? How to present the figure to a juggler so that he can learn and memorise it ?) led to ongoing research projects.
Impact
The show was presented more than 60 times in high schools, museums, theaters, festivals, etc., as well as three times in Istanbul, Turkey and once at the Art & Science festival Les Diableret, Switzerland. The show sometimes comes with a joint workshop for students.
Two M1 interships on the topic (Josué Moreau and Léo Kulinski) led to a paper which was awarded the Prix Sélection du Comité Scientifique de Paris-Saclay and a PhD. student (Léo Kulinski) funded by the CFM foundation.