Définitions formelles¶
Une grammaire décrit récursivement un ensemble d’objets. Elle est constituée d’un ensemble de règles ayant chacune un nom (chaîne de caractères). Le nom d’une règle est appelé symbole non-terminal ou plus simplement non-terminal de la grammaire.
Une règle de grammaire 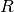 décrit un ensemble qui est
décrit un ensemble qui est
- soit un singleton dont le seul élément est un objet atomique et qui sera de poids 1 (par exemple la feuille d’un arbre).
- soit un ensemble dont le seul élément est un objet vide qui sera de poids 0 (par exemple la chaîne vide).
- soit l’union de deux ensembles décrit par deux non-terminaux
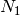 et
et 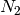 ;
; - soit en bijection avec le produit cartésien de deux ensembles décrit
par deux non-terminaux
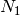 et
et 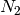 ; L’ensemble est alors construit à
partir des paires d’éléments
; L’ensemble est alors construit à
partir des paires d’éléments 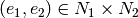 . Dans ce
cas, il faut de plus donner à Sage la bijection qui construit l’objet
correspondant à la paire
. Dans ce
cas, il faut de plus donner à Sage la bijection qui construit l’objet
correspondant à la paire 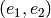 (concaténation pour les chaînes de
caractères où constructeur Node pour les arbres).
(concaténation pour les chaînes de
caractères où constructeur Node pour les arbres).
La taille ou poids d’un objet est le nombre d’atomes qu’il
contient. Le poids d’un élément correspondant à une paire 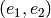 est
donc la somme des poids de
est
donc la somme des poids de 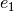 et de
et de 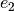 .
.
À chaque non-terminal on associe la taille du plus petit objet qui en dérive. Cette taille est appelé valuation du non-terminal.
Structures de données¶
On modélise chacun de ces ensembles décrits récursivement par un objet (au sens de la programmation orientées objets) Sage. Dans l’exemple des arbres binaires, l’objet treeGram["Tree"] modélise l’ensemble de tous les arbres binaires. Cet ensemble est construit comme l’union de deux sous ensembles modélisés par les objets treeGram["Node"] et treeGram["Leaf"]. La classe de treeGram["Tree"] est ainsi UnionRule, il est construit grâce à un appel au constructeur par UnionRule("Node", "Leaf").
Une grammaire sera stockées sous la forme d’un dictionnaire qui associe à une chaîne de caractère un objet. Dans le but de ne pas recopier plusieurs fois du code, on utilisera avantageusement la programmation objet et l’héritage. Ainsi chaque règle de grammaire sera un objet de la classe abstraite AbstractRule. On distingue deux types de règles de grammaires:
- les règles de constructions qui sont les objets des classes UnionRule et ProductRule qui dérivent de la classe abstraite ConstructorRule;
- les règles de constantes qui sont les objets des classes SingletonRule et EpsilonRule qui dérivent de la classe abstraite ConstantRule;
Voici un schéma de la hiérarchie de classe:
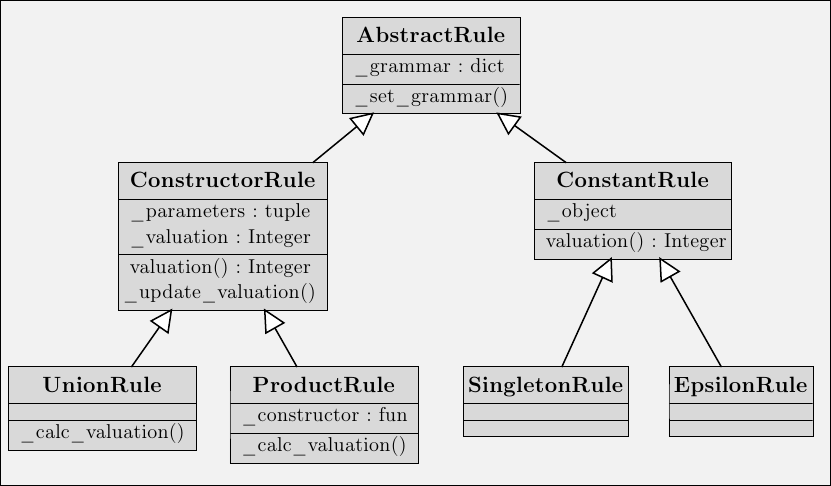
Voici la liste des constructeurs (méthodes __init__) des différentes classes avec les paramètres et leurs types:
- SingletonRule.__init__(self, obj) où obj est un object python quelconque;
- EpsilonRule.__init__(self, obj) où obj est un object python quelconque.
- UnionRule.__init__(self, fst, snd) où fst et snd sont deux non terminaux (de type string);
- ProductRule.__init__(self, fst, snd, cons) où fst et snd sont deux non terminaux et cons est une fonction qui prend un couple d’object et qui retourne un object.
En plus des méthodes listées dans ce diagramme, chaque classe devra implanter (ou bien hériter) les méthodes d’énumération suivantes: count, count_naive, list, unrank, random,dots
Le principal problème d’implantation provient du fait qu’une grammaire est un ensemble de définitions mutuellement récursives. Il y a donc un travail à faire pour «~casser des boucles infinies~» et s’assurer que la récursion est bien fondée. Voici quelques éléments permettant de résoudre ce problème:
- Pour les règles constructeur par exemple UnionRule("Node", "Leaf") les sous règles (ici: "Node" et "Leaf") ne sont connues que par les chaînes de caractères qui représentent les symboles non terminaux. Pour pouvoir associer ces chaînes aux objets associés, il faut que l’objet UnionRule("Node", "Leaf") ait accès à la grammaire.
- Au moment de la construction d’une règle, la grammaire qui va contenir la règle n’existe pas encore; il faut donc attendre que la grammaire soit complètement créée pour appeler la méthode _set_grammar sur chaque règle. C’est le rôle de la fonction init_grammar.
- La fonction init_grammar se charge également de calculer les valuations selon l’algorithme décrit plus bas.
Pour s’entraîner¶
- Donner la grammaire de tous les mots sur l’alphabet A, B.
- Donner la grammaire des mots de Dyck, c’est-à-dire les mots sur
l’alphabet
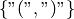 et qui sont correctement parenthésés.
et qui sont correctement parenthésés. - Donner la grammaire des palindromes sur l’alphabet A, B.
- Donner la grammaire des mots sur l’alphabet A, B qui contiennent autant de lettres A que de lettres B.
- Écrire une fonction qui vérifie qu’une grammaire est correcte, c’est-à-dire que chaque non-terminal apparaissant dans une règle est bien défini par la grammaire.