Introduction: quelques exemples

Les arbres binaires complets

Un arbre binaire complet est soit une feuille, soit un noeud sur lequel on a greffé deux arbres binaires complets. Une manière simple et rapide d’implanter la structure de donnée en Sage est de définir une variable formelle Leaf pour les feuilles et une fonction formelle Node d’arité 2 (demande la version 4.3 de sage):

sage: var("Leaf")               # variable formelle
sage: function("Node", nargs=2) # fonction formelle d'arité 2
sage: tr = Node(Leaf, Node(Leaf, Leaf))

On peut ainsi décrire l’ensemble des arbres binaires par les définitions récursives suivantes:

• l’ensemble "Trees" des arbres est la réunion disjointe (que l’on notera en Sage par le constructeur UnionRule) de deux ensembles: l’ensemble "Nodes" des noeuds et l’ensemble "Leaf" des feuilles;
• l’ensemble "Nodes" des noeuds est obtenu à partir de l’ensemble des paires d’arbres, c’est-à-dire le produit cartésien (noté par le constructeur ProdRule) de l’ensemble des arbres avec lui même;
• il n’y a qu’un seul arbre possible constitué d’une feuille. C’est le singleton (constructeur SingletonRule) "Leaf".

Une telle définition est appelée grammaire. On écrira en Sage la grammaire des arbres de la manière suivante:

sage: treeGram = {"Tree": UnionRule("Node", "Leaf"),
...               "Node": ProductRule("Tree", "Tree",
...                                   lambda (a, b) : Node(a, b)),
...               "Leaf": SingletonRule(Leaf)}
sage: init_grammar(treeGram)

Le but de ce projet est d’implanter un algorithme permettant de compter, d’engendrer automatiquement la liste ainsi que de tirer au hasard un des objets décrit par une grammaire de ce type : par exemple il y a 5 arbres binaires complets à quatre feuilles:

Ce que l’on peut obtenir par le programme

sage: treeGram['Tree'].count(4)
5

La liste des objets décrits par la grammaire peut ensuite être obtenue comme suit:

sage: for t in treeGram['Tree'].list(4): print t
Node(Leaf, Node(Leaf, Node(Leaf, Leaf)))
Node(Leaf, Node(Node(Leaf, Leaf), Leaf))
Node(Node(Leaf, Leaf), Node(Leaf, Leaf))
Node(Node(Leaf, Node(Leaf, Leaf)), Leaf)
Node(Node(Node(Leaf, Leaf), Leaf), Leaf)

Les mots de Fibonacci

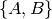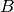On appelle mot de Fibonacci tout mot sur l’alphabet qui ne contient pas deux à la suite. Un tel mot 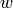est décrit par la grammaire suivante:

• soit 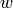est vide;
• soit 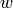est de la forme 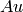où 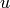est un mot de Fibonacci;
• soit 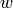est le mot ;
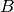• soit 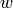est de la forme 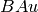où 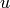est un mot de Fibonacci;

Ceci ce traduit en Sage par la grammaire:

sage: fiboGram = {"Fib"    : UnionRule("Vide", "Cas1"),
...               "Cas1"   : UnionRule("CasAu", "Cas2"),
...               "Cas2"   : UnionRule("AtomB", "CasBAu"),
...               "Vide"   : EpsilonRule(""),
...               "CasAu"  : ProductRule("AtomA", "Fib", "".join),
...               "AtomA"  : SingletonRule("A"),
...               "AtomB"  : SingletonRule("B"),
...               "CasBAu" : ProductRule("AtomB", "CasAu", "".join)}
sage: init_grammar(fiboGram)

Note

La commande "".join utilise la méthode join de la classe string qui concatène une liste ou un tuple de chaînes de caractères passé en argument:

sage: "".join(["ab","toto"])
'abtoto'

Voici la liste des mots de Fibonacci de longueur 3: AAA, AAB, ABA, BAA, BAB. Ce qui se calcule en Sage par

sage: fiboGram['Fib'].count(3)
5
sage: fiboGram['Fib'].list(3)
['AAA', 'AAB', 'ABA', 'BAA', 'BAB']

On peut de la même manière obtenir les 21 mots de Fibonacci de longueur 6:

sage: fiboGram['Fib'].list(6)
['AAAAAA', 'AAAAAB', 'AAAABA', 'AAABAA', 'AAABAB', 'AABAAA', 'AABAAB',
 'AABABA', 'ABAAAA', 'ABAAAB', 'ABAABA', 'ABABAA', 'ABABAB', 'BAAAAA',
 'BAAAAB', 'BAAABA', 'BAABAA', 'BAABAB', 'BABAAA', 'BABAAB', 'BABABA']