Un type est une classe de données ayant des propriétés communes. Les types sont utilisés pour aider à vérifier la correction des programmes, pour traduire les programmes en code exécutable (compilation), etc. C'est une notion fondamentale de l'informatique.
Dans la suite on va parler de types abstraits et de types concrets. On utilise les types abstraits pour la réalisation et les types concrets pour le codage. Les types concrets dépendent donc du langage de programmation que l'on utilise.
Un type abstrait est définit par :
Par exemple, on peut parler du type polynôme car tout polynôme peut être représenté par un degré et une suite de coefficients ci :
P(x) = cnxn + cn-1xn-1 + ... + c1x + c0
On peut avoir définir deux constructeurs :
Les opérations sur les polynômes peuvent être par exemple :
La déclaration peut se faire de la façon suivante :
type polynôme
{ constructeurs }
polynôme_nul
construire : polynôme * réel -> polynôme
{ opérations }
ajouter : polynôme * polynôme -> polynôme
éval : polynôme * réel -> réel
Les types concrets sont les types utilisés dans les langages de programmation. Alors qu'un type abstrait ne fait aucune supposition sur la représentation (le codage) des données du type, un type concret définit précisément l'implantation en machine des donnés de ce type, et les opérations prédéfinies qui sont disponibles.
Par exemple, un type abstrait "entier naturel" représente tout nombre >= 0, mais le type concret correspondant peut ne coder que les entiers entre 0 et 65535.
Les constructeurs et les opérations du type abstrait sont :
Dans le premier cas on parle de codage explicite et dans le second de codage implicite (vu en M1).
Dans un langage impératif, il faut déclarer le type de chaque variable, argument et valeur de retour de fonction du programme. Cela permet de vérifier que les constructions du programme sont correctes du point de vue des types. Nous reviendrons sur ce point en détail plus tard. Par exemple :
Les types concrets d'un langage de programmation sont
Dans la suite, on décrit un ensemble de types abstraits de base et composés qui correspondent (à peu près) aux types concrets usuels des langages impératifs. L'usage de ces types abstraits permettra de faciliter le codage implicite, qui est en général plus efficace à exécuter et plus concis à écrire.
Les types de base sont les types les plus simples et correspondent généralement aux entités manipulées directement par la machine.
Un type énuméré est défini par un domaine fini, décrit par l'énumération de ses éléments :
type carte
{constantes: }
pique, coeur, carreau, trèfle
On utilisera la notation plus concise suivante :
type carte = (pique, coeur, carreau, trèfle)
Les constante d'un type énuméré sont ordonnées, selon l'ordre de leur déclaration. Cela permet de définir un constructeur et 3 opérations sur tout type énuméré :
image : entier -> carte { constructeur }
ord : carte -> entier { indice dans l'énumération }
suivant : carte -> carte { élément suivant }
précédent : carte -> carte { élément précédent }
Cela nous permet de définir plusieurs invariants :
image(ord(x)) = x image(x) défini => ord(image(x)) = x suivant(x) = image(ord(x) + 1) précédent(x) = image(ord(x) - 1)
Le type booléen est prédéfini avec les valeurs faux et vrai. Les opérations de l'algèbre de Boole sont définies sur les booléens :
et : booléen * booléen -> booléen ou : booléen * booléen -> booléen non : booléen -> booléen
Le type caractère est prédéfini et représente l'ensemble des caractères imprimables. On note les constantes de ce type entre quotes :
'a', 'b', ..., 'z', '0', ..., '9', ';', '$', ...
Les types entier et réel sont prédéfinis. Les opérations arithmétiques et logiques usuelles sont définies sur ces types. Un entier peut être converti en réel et un réel peut être converti en entier (par troncature de la partie décimale).
Il y a une différence importante entre les types numériques abstraits, qui correspondent aux ensembles Z et R, et les types concrets, qui ne représentent qu'un ensemble fini de valeurs.
On définit un type intervalle à partir d'un type énuméré ou du type entier par la notation suivante :
type rouge = couleur dans [coeur .. carreau] type lettres = caracrtère dans ['a' .. 'z'] type dizaine = entier dans [10 .. 19]
Un type intervalle représente l'ensemble des constantes comprises entre les deux bornes de l'intervalle. Cette définition a un sens puisque les constantes d'un type intervalle sont toujours ordonnées.
Des règles particulières s'appliquent pour que les valeurs d'un type intervalle soient converties en valeur de leur type de base. Elles seront décrites plus tard.
Les types composés (appelés aussi types structurés) sont définis à partir d'un constructeur de type et d'un ou plusieurs types composants. Nous allons voir :
Un type produit est construit à partir d'un ensemble de composants. Chaque composant peut être extrait par une opération dite de projection :
type complexe
{ constructeur }
creer_complexe : réel * réel -> complexe
{ operations }
partie_réelle : complexe -> réel
partie_imaginaire : complexe -> réel
On appelle ce type un type enregistrement ou structure, les composants s'appellent des champs et on le note :
type complexe : produit re : réel im : réel fin
La notation pointée permet d'accéder aux champs
c.re = partie_réelle (c) c.im = partie_imaginaire (c)
On peut définir d'autres opérations sur les nombres complexes, comme le module et l'argument. (Noter que dans ce cas, on aurait pu représenter également un nombre complexe par son module et son argument, et avoir des opérations retournant les parties réelles et imaginaires.)
Les champs d'un enregistrement peuvent apparaitre en partie gauche d'une affectation :
c.re <- 1.0
Cela est équivalent à utiliser une nouvelle opération :
changer_partie_réelle : complexe * réel -> complexe
qui vérifie l'invariant :
partie_réelle (changer_partie_réelle (c, r)) = r.
L'affectation
c.re <- 1.0
est équivalente à
c <- changer_partie_réelle (c, 1.0)
Si l'on veut que le programme vu au premier cours puisse calculer des racines complexes, il suffit de modifier le cas d < 0 :
lexique c1, c2 : complexe début ... selon le cas d ... d < 0 : c1.re <- -b / 2*a c1.im <- sqrt(d) / 2*a c2.re <- -b / 2*a c2.im <- - sqrt(d) / 2*a
Le type tableau permet de représenter des fonctions à domaine fini : à chaque valeur d'un indice, le tableau associe une valeur ou élément de tableau.
Par exemple, on peut représenter les valeurs des cartes dans un jeu par :
type carte = (roi, dame, valet, as)
type valeur_carte
{ opérations }
valeur : tableau * carte -> entier
change_valeur : tableau * carte * entier -> tableau
A chaque carte, le tableau fait correspondre une valeur entière, accessible par l'opération valeur. On peut changer la valeur qui correspond à une carte par l'opération change_valeur. On peut se représenter un tableau comme un bloc-tiroirs dont chaque tiroir a une étiquette correspondant à son indice dans le tableau et dont le contenu est la valeur. Chaque tiroir est appelé un élément du tableau.
Un invariant de tableau est le suivant :
valeur (change_valeur (t, c, x), c) = x
Pour faciliter l'usage des tableaux, on les note comme suit :
type carte = (roi, dame, valet, as) type valeur_carte = tableau [carte] de entier
Le type de l'indice (ici carte) doit être un type énuméré ou intervalle. Le type des éléments (ici entier) peut être quelconque. Pour accéder aux éléments d'un tableau, on utilise la notation indicée :
t[i] = valeur (t, i)
Un élément de tableau peut apparaitre en partie gauche d'une affectation, ce qui permet de changer sa valeur :
t[i] <- v
est équivalent à
t <- changer_valeur (t, i, v)
L'accès à un élément de tableau n'est légal que si l'indice est compris dans l'intervalle défini à la déclaration du tableau.
Avec l'exemple des cartes :
type carte = (roi, dame, valet, as) lexique points : tableau [carte] de entier main : tableau [1..5] de carte total : entier début points[roi] <- 10 points[dame] <- 9 points [valet] <- 8 points [as] <- 1 pour i parcourant [1..5] faire main [i] <- carte_hasard total <- 0 pour i parcourant [1..5] faire total <- total + points[main[i]]
Lorsque l'on utilise comme indice un type intervalle d'entier, on retrouve pratiquement la notation indicée usuelle en mathématiques :
type vecteur = tableau [1..10] de réel somme_vecteur = vecteur * vecteur -> vecteur produit_scalaire = vecteur * vecteur -> réel fonction somme_vecteur (v1, v2) lexique v : vecteur i : 1..10 début pour i parcourant [1..10] v[i] <- v1[i] + v2[i] retourner v fonction produit_scalaire (p, q) lexique produit : réel i : 1..10 début produit <- 0 pour i parcourant [1..10] produit <- produit + p[i] * q[i] retourner produit
Cet exemple montre que l'on peut considérer le type tableau comme un type produit particulier. Pour des vecteurs à 3 dimensions, au aurait pu écrire :
type vecteur3D = produit x, y, z : réel fin somme3D = vecteur3D * vecteur3D -> vecteur3D fonction somme3D (v1, v2) lexique v : vecteur3D début v.x <- v1.x + v2.x v.y <- v1.y + v2.y v.z <- v1.z + v2.y retourner v
On voit que l'écriture est plus lourde, surtout si l'on avait des vecteurs à 10 dimensions. On remarque cependant la similitude entre la notation pointée et la notation indicée.
On peut définir des tableaux multi-dimensionnels (ou matrices) en utilisant le fait que les éléments d'un tableau peuvent eux-même être des tableaux :
type matrice= tableau [1..4] de tableau [1..4] de réel
L'accès se fait alors par :
lexique m : matrice début m[1][1] <- 0
Pour simplifier la notation, on peut écrire :
type matrice = tableau [1..4, 1..4] de réel lexique m : matrice début m[1, 1] := 0
On peut décrire un type "liste d'entiers" par le type abstrait suivant :
type Liste
{ constructeurs }
ListeVide
Cons : entier * Liste -> Liste
{ opérations }
Longueur : Liste -> entier
Tete : Liste -> entier
Fin : Liste -> Liste
Concat : Liste * Liste -> Liste
...
Une façon de représenter ce type abstrait par un type concret est d'utiliser un tableau qui va contenir les éléments de la liste :
type Liste = produit
longueur : entier
contenu : tableau [1..max] de entier
fin
fonction ListeVide : Liste
lexique
l : Liste
début
l.longueur := 0
retourner l
fin
fonction Cons (x : entier, l : Liste) : Liste
lexique
i : entier
res : Liste
début
{ il faudrait verifier que longueur <= max }
res.longueur := l.longueur + 1
pour i parcourant [1..l.longueur]
res.contenu [i+1] <- l.contenu [i]
retourner res
fin
...
Pour des raisons d'efficacité, on peut souhaiter que Cons ajoute l'élément dans la liste passée en argument plutôt que de retourner une nouvelle liste. Il serait alors judicieux de mettre les éléments dans la liste dans l'ordre inverse. Ainsi un ajout en tête de liste revient a ajouter l'élément a la fin du tableau :
procédure Cons (x : entier, donnée-résultat l : Liste)
début
{ il faudrait verifier que longueur <= max }
l.longueur := l.longueur + 1
l.contenu [l.longueur] <- x
fin
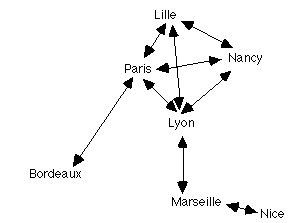
On veut représenter les relations entre un ensemble de gares SNCF. On se donne un type énuméré représentant les gares :
type gares = (Lille, Paris, Lyon, Nancy, Marseille, Bordeaux, Nice)
Considérons les liaisons suivantes :

On peut aussi les représenter dans un tableau à deux dimensions :
Lille Paris Lyon Nancy Marseill Bordeaux Nice
e
Lille X X
Paris X X X X X
Lyon X X X X
Nancy X X
Marseille X X X
Bordeaux X
Nice X
Ce tableau peut être représenter par un type tableau :
type ligne_SNCF = tableau [gares, gares] de booléen
Un tel graphe de connexions peut être utilisé pour répondre a un certain nombre de questions :
On peut aussi remplacer les croix par des distances kilométriques, et calculer ainsi la distance entre deux gares. On peut également avoir des liaisons à sens unique (la matrice n'est alors plus symétrique).
Le type somme permet de représenter des unions disjointes de domaines.
Par exemple, les solutions d'une équation du second degré peuvent être :
On peut définir le type abstrait suivant pour représenter ces solutions :
type solutions
{constructeurs}
réelles : réel * réel -> solutions
complexes : réel * réel -> solutions
double : réel -> solution
{opérations}
type_solution -> réelles | complexes | double
{invariants}
tag (réelles (r1,r2)) = réelles
tag (complexes (c1, c2)) = complexe
tag (double (d)) = double
On note un type somme de la façon suivante :
type type_solution = (réelles, complexes, double) type solutions = somme selon t : type_solution réelles : r1, r2 : réel complexes : c1, c2 : réel double : d : réel fin
Le type somme se comporte comme un type enregistrement : t, r1, r2, c1, c2, r sont des champs accessibles par la notation pointée. Le champ t est appelé "tag" ou "discriminant" car il indique dans quel sous-domaine on se trouve.
lexique racines : solutions début ... selon le cas d d > 0 : racines.t <- réelles racines.r1 <- ... racines.r2 <- ... d = 0 : racines.t <- double racines.d <- ... d < 0 : racines.t <- complexes racines.c1.re <- ... racines.c1.im <- ... racines.c2.re <- ... racines.c2.im <- ...
Il faut noter que l'accès à un champ n'est légal que si la valeur du discriminant correspond au sous-domaine qui contient ce champ. Ainsi, dans l'exemple ci-dessus, racines.d est illégal si racines.t vaut réelles.