


Dans ce chapitre, nous allons poser les bases d’une structure qui a beaucoup d’importance en informatique qui est celle de graphe. On a vu au chapitre précédent la notion de relation binaire, qui est une notion importante car c’est à partir d’elle qu’on définit d’autres notions comme celles de fonction, d’égalité, de relation d’ordre. Les graphes peuvent se voir comme une forme “concrète” de relations binaires sur un ensemble A : les éléments de A sont vus comme des points et deux éléments de A qui sont dans la relation sont reliés par un arc. La théorie des graphes va se poser des questions sur les chemins qui peuvent être construits dans le graphe (avec des contraintes comme de ne visiter les sommets une seule fois, ou de trouver le chemin le plus court entre deux sommets), ou encore la possibilité de colorier les sommets avec la contrainte que deux sommets liés ne sont pas de la même couleur. On s’intéresse à ces problèmes à la fois de manière abstraite mais aussi pour construire des algorithmes efficaces pour les résoudre. En effet beaucoup de problèmes concrets peuvent se modéliser comme des problèmes de graphes.
La théorie des graphes est un domaine complexe qui est l’objet de cours entiers spécifiques au niveau master et qui reste un sujet de recherche actif. L’objectif dans ce cours est de fournir les bases du vocabulaire sur les graphes qui est utile dans de nombreux contextes et d’illustrer les concepts sur des exemples élémentaires.
Nous commençons par donner quelques exemples de problèmes qui peuvent se ramener à des questions sur les graphes.
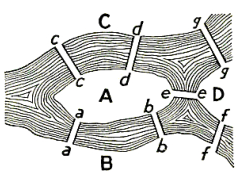
Dans la ville de Königsberg, peut-on faire un trajet qui passe une et une seule fois par chacun des sept ponts et revenir à son point de départ ?

Euler en 1736 répond à cette question en utilisant une modélisation comme un graphe.

La réponse est négative, pourquoi ?
Comment stocker des variables dans un nombre limité de registres pour faire un calcul ?
Les variables d,k,j seront utilisées dans la suite du programme.
| instructions | variables utiles |
| g:= mem [j+12] | k j |
| h:= k - 1 | j g k |
| f:= g * h | j g h |
| e:= mem[j+8] | j f |
| m:= mem[j+16] | j f e |
| b:= mem[f] | m f e |
| c:= e+8 | m b e |
| d:= c | m b c |
| k:= m+4 | m b d |
| j:= b | b d k |
| d k j |
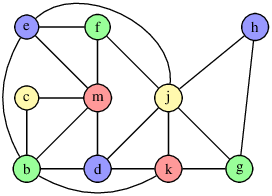
Les variables qui doivent être disponibles en même temps sont liées. Ranger les variables dans des registres revient à colorier le graphe.
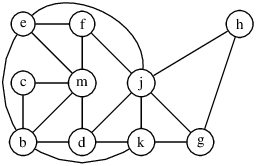
Si un sommet a moins de 3 voisins on peut toujours lui trouver une couleur.
Il y a beaucoup d’autres situations dans lesquelles la notion de graphe est importante, par exemple pour tout ce qui est la planification de trajets (dans une agence de voyage, ou bien à l’aide de GPS). La structure de graphe sera alors enrichie avec des annotations comme la durée du trajet ou son coût et on cherchera des chemins qui sont optimaux suivant certains critères.
Les graphes servent aussi à décrire des systèmes à états et transitions comme un système d’authentification avec un mot de passe que l’on ne peut essayer plus de trois fois ou encore un système de passage à niveau qui se ferme à l’approche d’un train. Les sommets du graphe vont correspondre à la description de l’état du système et les arètes correspondent à des changements d’états en fonction d’événements spécifiques.
On a vu sur les exemples, que dans un graphe on avait des points (appelés sommets) et des liens entre deux points (appelés arêtes). On a visualisé les graphes comme des dessins mais ce n’est qu’une représentation, la définition générale est plus abstraite.
On distingue deux sortes de graphes suivant s’ils sont orientés ou non. Dans un graphe orienté, les liens entre deux sommets ont une direction (que l’on représente en général par une flèche), c’est-à-dire qu’il est possible qu’il y ait un chemin de A à B sans qu’il y ait de chemin inverse de B à A.
Afin de ne pas dupliquer les définitions, on introduit une relation entre les arêtes et les sommets E(e,a,b) qui représente le fait que l’arête e a pour extrémités les sommets a et b. Dans le cas d’un graphe orienté, cela revient à dire que є(e)=(a,b) et dans le cas d’un graphe non orienté є(e)={a,b}
Réciproquement, si on se donne un graphe orienté (S,A,є), on peut toujours lui associer une relation binaire sur l’ensemble des sommets par la relation R =def {(a,b)∈ S× S|∃ e∈ A,є(e)=(a,b)} c’est-à-dire que l’on prend l’image de la fonction extrémité.
On peut montrer que les relations binaires correspondent exactement aux graphes orientés qui n’ont pas d’arêtes multiples (fonction extrémités injective). En particulier, s’il n’y a pas d’arêtes multiples, alors on peut se passer de “nommer” les arêtes, une arête est simplement caractérisée par le couple de ses extrémités.
Dans un graphe non orienté, d(a) est le cardinal de l’ensemble des arêtes qui ont a pour extrémité, les boucles sur a vont compter deux fois. On a donc
| d(a)=|{e∈ A|a∈ є(e)}|+|{e∈ A|є(e)={a}}| |
Dans un graphe orienté, on distingue les arêtes entrantes qui ont a comme destination et les arêtes sortantes qui ont a comme origine. Le degré entrant, noté d−(a), est le nombre d’arêtes entrantes alors que le degré sortant, noté d+(a), est le nombre d’arêtes sortantes. Le degré d’un sommet est la somme des degrés entrants et sortants.
| d−(a)=|{e∈ A|∃ b, (b,a)∈ є(e)}| d+(a)=|{e∈ A|∃ b, (a,b)∈ є(e)}| d(a)=d+(a)+d−(a) |
Preuve: Le chemin entre a et b s’écrit (a0,e1,a1,…,en,an) avec a0=a et an=b. Le chemin entre b et c s’écrit (b0,f1,b1,…,fp,bp) avec b0=b et bp=c. On forme le chemin entre a et c en concaténant les deux chemins puisque an=b=b0 : (a0,e1,a1,…,en,b,f1,b1,…,fp,bp) qui est bien un chemin de longueur n+p qui va de a à c. □
Preuve: Par récurrence sur la longueur du chemin. □
On considère les deux graphes ci-dessous, le premier est non-orienté, le second est orienté.
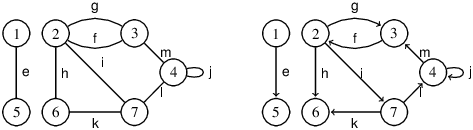
Indiquer les degrés des sommets 2 et 4.
Donner plusieurs chemins des sommets 4 à 6.
Ces graphes sont-ils fortement connexes ? Même question pour les sous-graphes dans lesquels on a enlevé les sommets 1 et 5.
Preuve: Soient deux sommets a et b et un chemin entre a et b noté (a0,e1,a1,…,en,an) avec a0=a et an=b. Si le chemin est élémentaire, la propriété est montrée. Sinon il existe deux indices i et j tels que i<j et ai=aj et en choisissant i le plus petit possible et j le plus grand possible on garantit que pour tout 0≤ k<i et j<l≤ n on a ak≠al. On considère le chemin obtenu en mettant bout à bout le sous-chemin allant de a0 à ai et le sous-chemin allant de aj à an qui est élémentaire. □
On est souvent intéressé par revenir à son point de départ.
Preuve: On regarde le cas des graphes non-orientés.
S’il n’y a pas de points isolés alors le cycle eulérien qui passe par toutes les arêtes passe aussi par tous les sommets. Le graphe est donc fortement connexe puisque deux sommets sont reliés par la portion du circuit entre ces deux sommets. Lorsqu’un sommet apparait dans le chemin il y a une arête qui entre et une qui sort, c’est évident pour les sommets qui sont au milieu du chemin mais c’est aussi vrai pour les extrémités puisque le départ et l’arrivée sont les mêmes, donc le degré de chaque sommet est pair.
Montrons que tout graphe G fortement connexe dont les sommets sont de degré pair à un cycle eulérien.
On fait la preuve par récurrence sur le nombre d’arêtes du graphe. S’il n’y a pas d’arêtes alors comme il n’y a pas de point isolé le graphe est vide et le résultat est vrai.
Supposons que le résultat est vrai pour tout graphe ayant moins de n arêtes et montrons qu’il est vrai pour un graphe qui à n+1 arêtes. On distingue plusieurs cas
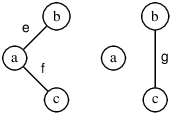
Il ne peut pas y avoir d’arête qui va d’un sommet de G′a à un sommet de G′b sinon tous les sommets de G′ seraient liés. Donc les arêtes de G′ sont soit dans G′a soit dans G′b. Les degrés des sommets dans G′a et G′b sont les mêmes que ceux des sommets dans G′ et sont donc pairs. Le nombre d’arêtes dans chacun de ces graphes est plus petit que le nombre d’arêtes de G′ et donc que n. L’hypothèse de récurrence s’applique aux deux graphes. On obtient deux cycles eulériens Ca qui couvre les arêtes de G′a et Cb qui couvre les arêtes de G′b. Il suffit de prendre le cycle Cb qui contient l’arête g, par exemple dans la direction bgc et on remplace cette arête par bfCagc. On a bien ainsi couvert toutes les arêtes du graphe G.
□
On va proposer plusieurs représentations concrètes des graphes (finis) qui pourront donner des pistes pour une représentation en machine. On s’intéresse ici à des graphes finis (nombre fini de sommets et d’arêtes).
Il est donc toujours possible de représenter les sommets et les arêtes par des entiers.
La matrice d’incidence est une matrice qui représente la relation entre les arêtes et ses extrémités. Cette matrice a pour lignes les sommets et comme colonnes les arêtes.
Dans le cas d’un graphe non orienté, la matrice d’incidence J contient des entiers entre 0 et 2. On a J(a,e)=0 si a∉є(e) J(a,e)=2 si є(e)={a} et J(a,e)=1 dans les autres cas, c’est-à-dire si a ∈є(e) et є(e)≠{a}.
L’exemple précédent du graphe non orienté a la matrice d’incidence suivante.
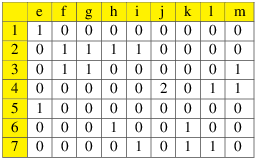
Dans le cas d’un graphe orienté on utilisera deux matrices qui ne contiennent que des 0 et des 1. La matrice d’incidence sortante J+ et la matrice d’incidence entrante J− telles que J+(a,e)=1 si et seulement si il existe b∈ S tel que є(e)=(a,b) et J−(b,e)=1 si et seulement si il existe a∈ S tel que є(e)=(a,b).
L’exemple précédent du graphe orienté a la matrice d’incidence sortante et la matrice d’incidence entrante suivantes.
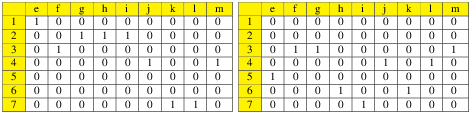
Une autre manière de représenter le graphe G =def (S,A,є) est de le voir comme une matrice carrée indicée par l’ensemble des sommets S et telle que sur la ligne a et la colonne b on met l’ensemble des arêtes qui ont a et b comme extrémités, c’est-à-dire l’ensemble {e∈ A| E(e,a,b)}. Si on s’intéresse à une représentation des graphes à isomorphisme prêt, il n’est même pas nécessaire de conserver dans la matrice l’ensemble des arêtes, il suffit de conserver leur nombre. En effet on peut toujours à partir de la matrice, compter le nombre total d’arêtes et ensuite les numéroter.
Les exemples de graphes donnés précédemment ont pour matrice d’adjacence :
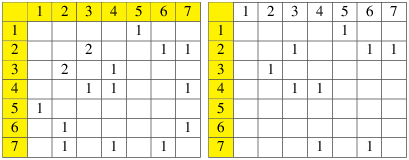
Un graphe non orienté est représenté par une matrice symétrique.
Soit un graphe G sur l’ensemble de sommets 1,…,n et α sa matrice d’adjacence.
Il y a un chemin entre deux sommets, si et seulement si il y a un chemin élémentaire qui ne passe pas deux fois par le même sommet. Comme il y a n sommets, ce chemin a au plus n−1 arêtes. Il n’est donc pas utile de chercher etre les deux points des chemins de longueur plus que n−1.
Si on multiplie α par elle même on obtient une matrice α2 telle que α2(i,j)=Σk=1k=nα(i,k)α(k,j). Ce nombre représente exactement le nombre de chemins de longueur 2 entre i et j. On montre aisément par récurrence sur k que la matrice αk a comme coefficient (i,j) le nombre de chemins de longueur k entre les sommets i et j.
Multiplier deux matrices carrées de taille n nécessite par la méthode naive n3 opérations et donc déterminer s’il y a un chemin entre deux points du graphe en calculant αn−1 par une méthode naive de calcul d’exponentiel prendra de l’ordre de n4 opérations. En calculant αn avec une méthode dichotomique, on peut ne faire que log2(n) multiplications.
On peut aussi vouloir simplement savoir s’il existe un chemin entre deux points. C’est l’algorithme de Warshall. L’idée est de construire par récurrence sur k une matrice βk qui contient des booléens et telle que βk(i,j)=V si et seulement si il y a un chemin de i à j dont les nœuds intermédiaires sont dans l’ensemble {1,…,k}.
Dans le cas où k=0 il n’y a pas de nœud intermédiaire et donc il y a un chemin si et seulement si il y a une arête et donc β0(i,j)=(α(i,j)≠0).
Maintenant on suppose que l’on a calculé βk et on veut calculer βk+1. Il y a un chemin de i à j dont les nœuds intermédaires sont dans l’ensemble {1,…,k+1}. Deux cas sont possibles,
On a donc βk+1(i,j)=βk(i,j)∨ βk(i,k+1)∧βk(k+1,j).
On peut donc calculer βk+1 en n2 opérations et donc finalement savoir s’il y a un chemin entre deux points en calculant βn−1 en n3 opérations.


