Calcul propositionnel

Le calcul propositionnel est un système logique dans lequel on se donne un ensemble X de variables propositionnelles qui peuvent être vraies ou fausses et on considère des formules logiques construites à partir de ces variables avec des connecteurs logiques {¬,∨,∧,⇒,⇔} (pas de quatificateur).

Ce système peut paraitre simpliste, mais il est néanmoins très utile et utilisé. En effet beaucoup de problèmes peuvent être modélisés ainsi, quite à introduire un très grand nombre de variables. Les problèmes de validité (ma formule est-elle toujours vraie, quelles que soient les valeurs des variables) ou de satisfiabilité (est-ce qu’il existe des valeurs des variables pour lesquelles la formule est vraie) sont décidables. Même si la complexité de ces problèmes est élévée (c’est un problème NP complet, pour lequel s’il existe un algorithme polynomial alors le fameux problème de complexité P=NP est résolu).

Dans ce chapitre, on va étudier le calcul propositionnel du point de vue de l’informaticien qui veut implanter un système de raisonnement sur ordinateur et donc qui va faire un certain nombre de manipulations symboliques.

6.1 Syntaxe

Comme pour toute structure de terme, on a de manière associée la possibilité de définir des fonctions par des équations récursives sur la structure de la formule et on peut aussi raisonner par récurrence structurelle sur la formule.

Exercice 1

Donner la forme arborescente de la formule p ∧ q ⇒ ¬ r ⇒ ⊥ avec p, q et r des variables propositionnelles.
Donner les équations d’une fonction récursive nb-neg qui compte le nombre de négations dans une fomule.
Enoncer le principe de récurrence structurelle pour des formules dont les seuls connecteurs binaires sont ∧ et ∨.

6.2 Interprétation et modèles

On notera B l’ensemble des booléens {V,F} qui représentent les valeurs de vérité vrai et faux, parfois aussi notées 1,0.

C’est une algèbre de Boole avec l’ordre F≤ V. La borne supérieure correspond au ou logique et la borne inférieure au et logique.

Pour interpréter une formule propositionnelle comme une valeur de vérité, il faut au préalable savoir comment on interprète les variables propositionnelles. En effet une variable propositionnelle est une inconnue donc peut très bien être remplacée par une proposition vraie ou une proposition fausse ou même par une formule qui comporte elle-même des variables propositionnelles et donc qui peut parfois prendre la valeur vraie et parfois la valeur faux.

Définition 1 (Interprétation) Une interprétation est une fonction qui associe une valeur de vérité à chaque variable propositionnelle. C’est donc une fonction I ∈ X → B. On l’écrira sous la forme {p₁↦ b₁,…,p_n↦ b_n} avec p_i∈ X une variable propositionnelle et b_i∈B la valeur booléenne V ou F correspondante.

Étant donnée une interprétation I∈ X → B, on peut calculer la valeur de vérité de n’importe quelle formule propositionnelle.

Exemple 1 Soit la formule P définie comme ((x ⇒ y) ⇒ x) ⇒ x et I l’interprétation {x↦ F,y↦ V}. On a val(I,x ⇒ y)=V donc val(I,(x ⇒ y) ⇒ x)=F et donc val(I,((x ⇒ y) ⇒ x) ⇒ x)=V. Cette formule est en fait une tautologie (vraie pour toute interprétation).

La valeur d’une formule ne dépend que de la valeur de l’interprétation pour les variables qui apparaissent dans la formule. Si deux interprétations I₁ et I₂ coïncident (ont la même valeur) sur l’ensemble des variables propositionnelles d’une formule P alors val(I₁,P)=val(I₂,P).

Définition 2 Une formule P est valide si elle est vraie pour toute interprétation (on dit aussi que c’est une tautologie). Elle est satisfiable s’il existe une interprétation pour laquelle elle est vraie et elle est insatisfiable sinon, c’est-à-dire quand la formule est fausse quelle que soit l’interprétation.

Proposition 1 La formule P est valide (resp. insatisfiable) si et seulement si la formule ¬ P est insatisfiable (resp. valide).

Une formule propositionnelle fait apparaître seulement un nombre fini n de variables propositionnelles. Il y a 2ⁿ interprétations différentes pour ces variables propositionnelles, on peut donc connaître la validité d’une formule en calculant la valeur pour chacune de ces interprétations. Si on s’intéresse uniquement à la satisfiabilité, il suffit d’exhiber une interprétation pour laquelle la formule est vraie.

Définition 3 (Modèle d’une formule) Un modèle d’une formule P est une interprétation I des variables de cette formule qui rend la formule vraie c’est-à-dire telle que val(I,P)=V.
On étend la notion de modèle à un ensemble de formules (fini ou infini) E, I est un modèle si pour toute formule P∈ E, on a val(I,P)=V.

Exemple 2 Soit la formule P définie comme ¬(x∧ y) ⇒ ¬ y. L’interprétation {x↦ V; y ↦ F} est un modèle, par contre {x↦ F; y ↦ V} n’en est pas un.

Equivalences

On utilise plusieurs connecteurs booléens mais il y a des équivalences entre ces connecteurs.

On écrira P≡ Q si les valeurs de vérité de P et Q coïncident pour toute interprétation (i.e. ∀ I∈ X →B, val(I,P)=val(I,Q)).

6.3 Formes normales

Lois algébriques

L’ensemble des booléens avec les opérations de conjonction et de disjonction forme une Algèbre de Boole.

Il en est de même de l’ensemble des formules quotienté par la relation d’equivalence.

Lois de de Morgan

Les lois de de Morgan établissent le comportement de la négation par rapport aux autres connecteurs :

Équivalence entre connecteurs. Certains connecteurs peuvent se définir en fonction d’autres :

Les équivalences mises en évidence ci-dessus montrent que la même propriété peut s’exprimer de plusieurs manières différentes. Cette redondance est intéressante pour l’expressivité (exprimer les notions le plus clairement possible en utilisant un vocabulaire riche) mais par contre peut être un frein au traitement informatique (comparaison, cas multiples à considérer).

On a par exemple déjà établi dans le paragraphe précédent que l’on pouvait se passer des connecteurs ⇒ et ⇔ en utilisant à la place les connecteurs ¬, ∨ et ∧. On constate que dans le cas de l’équivalence, la formule transformée est deux fois plus grosse que la formule initiale, donc l’élimination du connecteur peut avoir un coût important.

Aussi on s’intéresse à établir qu’il existe des formes canoniques pour les formules propositionnelles.

Fonctions booléennes

De manière générale une formule P qui dépend de n variables propositionnelles p₁,…,p_n peut se voir comme une fonction booléenne à n arguments dans Bⁿ→ B. C’est la fonction qui au n-uplet de booléens b₁,…,b_n associe la valeur boolénne val({p_i↦ b_i}_{i=1… n},P) correspondant à la valeur de vérité de la formule P dans l’interprétation qui associe la valeur b₁ à la variable propositionnelle p₁, la valeur b₂ à la variable propositionnelle p₂… On notera F(P) cette fonction.

Les notions de validité, satisfiabilité, insatisfiabilité d’une formule sont de fait des propriétés de la fonction booléenne associée : P est valide (resp. insatisfiable) si et seulement si F(P) est la fonction constante qui vaut T (resp. F). De même l’équivalence de deux formules correspond à l’égalité des fonctions booléennes associées, on a :

Une question naturelle est, étant donnée une fonction booléenne f quelconque à n arguments, peut-on trouver une formule propositionnelle P à n variables propositionnelles qui lui corresponde, c’est-à-dire telle que f= F(P).

La réponse est positive et même si on se restreint à des classes particulières de formules propositionnelles.

Forme normale de négation

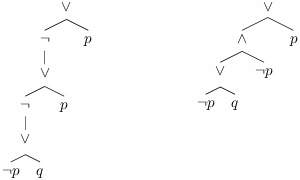
Les lois de de Morgan rappelées dans la section 6.3 permettent de propager la négation vers les variables propositionnelles.

Définition 4 (Littéral) On appelle littéral une formule qui est soit une formule atomique, soit la négation d’une formule atomique.

Proposition 2 Toute formule propositionnelle est équivalente à une formule propositionnelle qui ne comporte pas de connecteur ¬ sauf dans un littéral et seulement des conjonctions et disjonctions.

Une telle formule est dite en forme normale de négation.

Preuve: Pour résoudre ce problème, on construit deux fonctions de manière récursive : fnn (resp. neg) qui étant donnée une formule quelconque P, construit une formule en forme normale de négation équivalente à P (resp. équivalente à ¬ P).

On montre ensuite par récurrence sur la formule que fnn(P) et neg(P) sont en forme normale de négation et que de plus fnn(P)≡ P et neg(P)≡ ¬ P □

Exemple 3 Soit la formule ((p ⇒ q) ⇒ p) ⇒ p dans laquelle on élimine les implications, cette formule devient : ¬ (¬ (¬ p ∨ q) ∨ p) ∨ p. On peut ensuite repousser les négations en commençant par l’extérieur:

On obtient la formule : ((¬ p ∨ q) ∧ ¬ p)) ∨ p qui peut se simplifier en ¬ p ∨ p puis en ⊤.

Forme normale conjonctive

Définition 5 (Clause) On appelle clause une formule propositionnelle qui n’utilise que des littéraux et la disjonction.

Comme la disjonction est associative et commutative, la clause peut toujours s’écrire de la forme l₁∨ l₂∨… ∨ l_n avec l_i un littéral et on peut réarranger les littéraux dans l’ordre que l’on veut (par exemple en ordonnant les variables propositionnelles, puis pour chaque variable en mettant d’abord les littéraux positifs puis les négatifs). Par ailleurs, on a P∨ P≡ P et P∨ ¬ P≡ ⊤. On peut se ramener à une clause dans laquelle chaque variable propositionnelle apparaît au plus une fois sous forme positive ou négative.

Proposition 3 Une clause est équivalente à ⊤ ou bien à une clause qui est une disjonction de variables propositionnelles (simples ou niées) dans laquelle chaque variable apparaît au plus une fois.

Preuve: Si une variable propositionnelle p apparaît deux fois sous forme positive ou deux fois sous forme négative, alors en utilisant P∨ P≡ P on peut retirer une des occurrences sans changer la valeur de la formule. Si une variable propositionnelle apparaît une fois sous forme positive et une fois sous forme négative alors, en utilisant p∨ ¬ p ≡ ⊤, on peut remplacer ces deux occurrences par la formule ⊤. Une clause qui contient ⊤ est simplement équivalente à ⊤. □

Une clause est donc caractérisée par un ensemble de variables propositionnelles, chacune associée à une polarité pour indiquer si elle apparaît en position positive ou négative.
Par convention, la clause associée à un ensemble vide de littéraux est interprétée comme la formule fausse ⊥.

Proposition 4 Soient L₁ et L₂ des ensembles de littéraux, si L₁⊆ L₂ alors la clause correspondant à L₂ est une conséquence logique de la clause correspondant à L₁.

Preuve: Si L₁ est un ensemble vide alors la clause correspondante est ⊥ et toute propriété est conséquence logique de ⊥. Sinon soit C₁ (resp. C₂, resp. C₃) la clause correspondant à L₁ (resp. L₂, resp. L₂ ∖ L₁). On a C₂ ≡ C₁ ∨ C₃ et donc comme C₁ ∨ C₃ est une conséquence logique de C₁, on en déduit que C₂ est une conséquence logique de C₁. □

Définition 6 (Forme normale conjonctive) Une formule est dite en forme normale conjonctive si elle s’écrit comme une conjonction de clauses. Par convention, la conjonction d’un ensemble vide de formules est interprétée comme la formule vraie ⊤.

Proposition 5 Toute formule P admet une forme normale conjonctive, c’est-à-dire qu’il existe une formule Q équivalente à P et qui est en forme normale conjonctive.

Pour démontrer ce résultat, nous allons utiliser une autre propriété qui dit que toute fonction booléenne f à n arguments peut être associée a une formule Q en forme normale conjonctive telle que f= F(Q). En appliquant ce résultat à la fonction booléenne F(P) associée à P, on aura démontré le résultat de la proposition 5.

Proposition 6 Pour toute fonction booléenne f à n arguments, on peut trouver une formule Q en forme normale conjonctive telle que f= F(Q).

Preuve: On s’intéresse à l’ensemble Z des n-uplets pour lesquels la fonction f est fausse, c’est-à-dire

Dans la table de vérité, il suffit de s’intéresser aux lignes où la valeur de la formule est F. L’ensemble Z est fini. Si cet ensemble est vide alors f= F(⊤) qui est en forme normale conjonctive. On cherche une formule propositionnelle Q qui dépend des variables p₁,…,p_n correspondant à f. La variable propositionnelle p_i correspond à la propriété “le i-ème argument de f est vrai”. La propriété Q doit être vraie lorsque la fonction est vraie et donc doit exprimer que les arguments ne sont pas dans Z. Pour un élément (b₁,…,b_n), la formule qui dit que les arguments ne correspondent pas à cette valeur est l₁ ∨ l₂ ∨ … ∨ l_n avec l_i=p_i si b_i=F et l_i=¬ p_i si b_i=V. Cette formule est une clause. Il suffit ensuite de prendre la conjonction des clauses pour chaque élément de Z. □

Exemple 4 Soit la formule P =^def (p ⇒ q) ⇒ (¬ p ∧ q), on commence par écrire la table de vérité :

p	q	¬ p ∧ q	p ⇒ q	(p ⇒ q) ⇒ (¬ p ∧ q)
V	V	F	V	F
V	F	F	F	V
F	V	V	V	V
F	F	F	V	F

Les lignes qui nous intéressent sont la première et la dernière et on doit exprimer une formule qui dit exactement que l’on n’est pas dans un de ces deux cas.

La formule qui dit que l’on n’est pas dans le cas de la ligne 1 est ¬ p ∨ ¬ q et la formule qui dit que l’on n’est pas dans le cas de la ligne 4 est p ∨ q.

La forme normale conjonctive est donc (¬ p ∨ ¬ q) ∧ (p ∨ q).

En général, on ne veut pas construire la table de vérité et on procède donc par équivalences en construisant la forme normale de négation puis en utilisant la distributivité.

Exemple 5 Mettre en forme normale conjonctive la formule

(¬ (p₁∧ q₁)⇒ (p₂∧ q₂)) ∨ (p₃∧ q₃)

Les formes normales peuvent être exponentiellement plus grandes, on utilise parfois d’autres procédures qui introduisent des variables supplémentaires et ne sont pas équivalentes mais sont équi-satisfiables (la formule initiale est satisfiable si et seulement si la formule transformée est satisfiable, ce qui suffit pour les procédures de démonstration automatique.

Forme normale disjonctive

Définition 7 (Forme normale disjonctive)

Une conjonction élémentaire est une formule uniquement composée de littéraux et de conjonctions.
Une formule P est en forme normale disjonctive si elle s’écrit comme une disjonction de conjonctions élémentaires.

Proposition 7 Pour toute formule propositionnelle P, il existe une formule Q équivalente en forme normale disjonctive.

Preuve: Comme précédemment, on peut construire la table de vérité de la formule P par rapport aux variables propositionnelles {p₁,…,p_n}. On s’intéresse à l’ensemble O des n-uplets (b₁,…,b_n), pour lesquels la table de vérité donne la valeur vrai. Pour chaque ligne on construit une conjonction élémentaire l₁ ∧ l₂ ∧ … ∧ l_n avec l_i=p_i si b_i=V et l_i=¬ p_i si b_i=F. Il suffit ensuite de prendre la disjonction de ces formules pour trouver une formule équivalente à P. □

Exemple 6 En reprenant la formule P de l’exemple 4, on obtient la forme normale disjonctive :

(p∧ ¬ q) ∨ (¬ p ∧ q)

Si une formule est en forme normale disjonctive alors il est facile de trouver un modèle. On suppose que les branches de la disjonction sont en forme “simplifiée” c’est-à-dire qu’une variable propositionnelle apparaît dans un seul littéral. Il suffit de choisir une des branches de la disjonction. Pour chaque variable propositionnelle x qui apparaît dans un littéral l on prend dans le modèle x↦ V si l=x et x↦ F si l=¬ x. Il peut arriver qu’il n’y ait aucune composante en forme simplifiée: c’est le cas où la formule initiale est équivalente à ⊥ et donc il n’y a pas de modèle.

Cependant, la mise en forme normale n’est pas forcément la meilleure manière de trouver un modèle. En effet, cette forme normale peut être exponentiellement plus grosse que la formule initiale. C’est le cas par exemple de la formule (a₁∨ b₁) ∧…∧ (a_n ∨ b_n) qui a 2n variables et 2n−1 connecteurs. La forme normale disjonctive s’écrit ∨_{x_i∈{a_i,b_i}}(x₁∧… ∧ x_n). Il y a donc 2ⁿ disjonctions.

Exemple 7 (Sudoku) On peut aussi exprimer un problème directement sous la forme d’un ensemble de clauses. Par exemple dans le cas du Sudoku, on a 9³ variables X_ij^k pour i,j,k∈ [1,9]. L’interprétation est que X_ij^k est vrai si le chiffre k est sur la i-ème ligne et la j-ème colonne.

Les clauses expriment

Il y a au moins un chiffre sur la case i,j
S’il y a le chiffre k sur la case i,j alors k n’apparaît pas sur une case i′,j′ en conflit avec i,j (même ligne, colonne ou carré).

6.4 Démonstration Automatique

Satisfiabilité

On va s’intéresser ici à l’implantation d’une procédure de décision de la satisfiabilité : étant donnée une formule propositionnelle, existe-t-il une interprétation (des valeurs pour les variables) qui rende la formule vraie (qui soit donc un modèle). La version proposée ici est une version naive de l’algorithme DPLL (du nom de ses inventeurs Davis, Putnam, Logemann et Loveland) .

Cette procédure permet de dire si une formule en forme normale conjonctive (représentée par un ensemble de clauses) est satisfiable. Pour cela, l’algorithme cherche à construire une interprétation qui rend la formule vraie.

Une formule en forme normale conjonctive est vue comme un ensemble de clauses. Chaque clause est un ensemble de littéraux. On note l une clause qui ne contient que le littéral l et ⊥ la clause vide qui ne contient pas de littéraux.

L’algorithme DPLL travaille sur des problèmes de la forme : I ≫ Δ dans laquelle

On note Δ,C le problème qui contient toutes les clauses de Δ plus la clause C. Le but de l’algorithme est de construire une interprétation qui étend I, c’est-à-dire de la forme {x₁↦ b₁;…;x_n↦ b_n;x_n+1↦ b_n+1… x_p↦ b_p} et qui rend vraies toutes les clause C_i.

Il y a deux cas triviaux. Le premier cas s’il n’y a plus de clauses, l’interprétation I répond au problème. Le second cas si l’une des clauses C_i est la clause vide alors le problème n’a pas de solution. Cela correspond aux deux règles :

Par ailleurs on peut simplifier les problèmes : lorsque l’interprétation I fixe la valeur de la variable x, alors les clauses C qui contiennent un litteral l de la forme x ou ¬ x se simplifient :

Maintenant si aucune des règles précédentes ne s’applique, alors il faut préciser l’interprétation en choisissant une valeur pour une nouvelle variable. Un cas simple est si une clause ne contient qu’un seul littéral alors pour que la clause soit vraie il faut choisir la valeur de la variable pour rendre ce littéral vrai. Ceci s’exprime par les règles suivantes :

Si maintenant, il n’y a aucune clause réduite à un littéral, alors il n’y a pas de choix évident. On va donc choisir une variable qui n’a pas encore de valeur et explorer les deux branches : celle où cette variable est interprétée par V et celle où elle est interprétée par F.

On part d’un ensemble de clauses Δ et d’une interprétation vide. On construit un arbre en utilisant les règles précédentes et on cherche à arriver à une feuille de succès de la forme I≫∅. L’interprétation I est une solution de notre problème, elle rend vraie l’ensemble des clauses Δ.

Si toutes les feuilles de l’arbre correspondent à des conflits alors l’ensemble de clauses initial n’est pas satisfiable.

Exercice 2

Appliquer l’algorithme précédent aux formules
1. (¬ p ∨ ¬ q ∨ ¬ r) ∧ (¬ p ∨ q ∨ r) ∧ (p ∨ q ∨ ¬ r)
2. (p∨ r) ∧ (¬ q ∨ p) ∧ ¬ p ∧ ¬ r
Justifier que la construction de l’arbre par les règles DPLL est toujours finie (trouver une quantité qui diminue le long des branches de l’arbre).
Montrer que les règles de DPLL sont correctes. C’est-à-dire que si un arbre DPLL de racine I≫ Δ contient une feuille de succès J ≫ ∅ alors l’interprétation J étend l’interprétation I (c’est-à-dire que I(x)=J(x) pour toutes les variables x qui apparaissent dans I) et l’interprétation J rend vraies toutes les clauses de Δ.
En déduire une méthode pour trouver un modèle d’une formule.
Peut-on utiliser cette méthode pour prouver la validité d’une formule ?

6 Calcul propositionnel