Indirect addressing problems are either gathers, e.g. A(i) = B(L(i)), or scatters,e.g. A(L(i)) = B(i), or both. We make the following assumptions, and we later relax some of them:
then 
Assumption (1) is mandatory for parallel scatters to be determistic. For gathers, assumption (1) has connections with the existence of spatial locality in the sense of multiple uses of the same data. In the indirect addressing framework, reusing implies that L is many-to-one. Hence the scope of the sorting method is outside the field of the inspector/executor scheme with respect to data patterns.
If assumptions (1) and (2) hold, it is obvious that the scatter reduces to sorting array B following the keys L. More precisely, the idea is to sort L, and let the corresponding items B follow their key across the various steps of the sorting algorithm, as usual in sorting. Hence, we cannot relax the assumption that B and L have the same size and are identically distributed (e.g. are aligned onto the same TEMPLATE in HPF dialect).
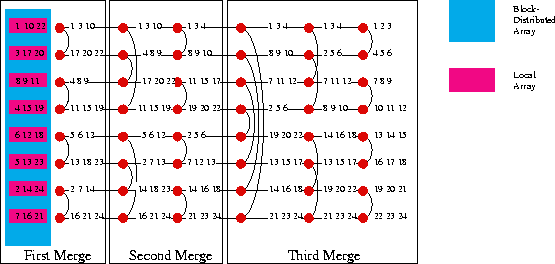
Figure 1: Odd-Even Merge Sort. Lines describes the
comparison-exchange. The larger value goes ``down'' and the smaller
values goes ``high''
The most important point to choose the sorting algorithm is that it should be recursive in nature, lead to a problem for which a fast algorithm is known when recursion falls into a sequential process, and be well-balanced. Due to the high cost of network access, the sorting algorithm must also take into account the network topology, so as to avoid contention. A candidate fulfilling all these requirements is the classical Odd-Even Merge Sort (OEMS). A lot of theoretically better parallel sorting algorithms do exist, that parallelize fast sequential algorithms (quicksort, radix sort) or are inherently parallel (flashsort) [1, 3]. All these algorithms involve global operations such as multi-cast or multi-scan. Monolithic parallel architectures such as the CM-5 or T3-E efficiently support global operations. But our target machine, an IBM SP-2, and commodity-based high-speed networks of workstations, do not markedly optimize the global operations. As OEMS only uses point-to-point communication and has low control overhead, we choosed it for our implementation.
We recall the principle of OEMS for sorting n items when n is a power of 2, but the same algorithm works for any n. The merge part of the algorithm (Odd-Even Merge) merges two sorted lists by splitting up the lists into their odd and even parts, recursively merging the alternate sublists, and merging the resulting two sublists by comparison-exchange of adjacent values. OEMS starts by Odd-Even Merging pairs of n sub-arrays of length 1 to form n/2 sorted sub-arrays of length 2, then merges the sorted sub-arrays to form n/4 sorted sub-arrays of length 4 and so on (fig. 1). Thus, all recursions end up either in a sorting problem or in a merging problem, which can be computed sequentially when a processor holds an entire sub-array.
We call local array the part of a distributed array that a given processor holds. Assuming that A, B and L are block distributed, OEMS can be implemented in the following way (fig. 1 shows an example): the first step sorts the local arrays independently in parallel; the next steps iterate over the steps of the Odd-Even Merge sort algorithm, where each comparison-exchange operation is replaced by merging the corresponding arrays; the lower numbered processor keeps the lower half of the resulting array and the higher processor the higher half.
Block distribution is straightforward, because the lexicographic order (processor, offset in local array) is identical to the linear order of indices. However, sorting with any distribution in not difficult: the only difference is in the order used for the comparisons, which should always be the lexicographic order (processor, offset in local array) corresponding to the distribution of A. For instance, if A has length 16 and is cyclically distributed onto four processors, the order is:
{1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15, 4, 8, 12, 16}.
Computing at run-time the comparisons following this order can be costly if the block size k for cyclic(k) distributions or the number of processors P are not powers of 2. The simplest way to avoid these costly and redundant computations is to precompute in parallel the index of each data in L in the target order (e.g., in the previous example, the index of 9 is 3, the index of 13 is 4 and so on), to store it in a temporary array and to use the temporary in place of L in the sorting process.
Let 
be the size of A. If and P are powers of 2, the
assumption that A has the same size than B can be relaxed. First, OEMS is
applied. The items of L and B have not reached their destination, but
L is sorted, so that the remaining work is only a what is known in
routing theory as a
spreading problem: routing a set of data located on a contiguous
set of the inputs of a indirect routing network so that their
relative order remains unchanged. In particular, greedy routing on a
butterfly network solves the spreading problem in one traversal. The
next step for our problem is to emulate
a butterfly network of size onto the processor set. This cost
only 
communnication steps. Emulating
means that the traversal of one stage of the network is emulated by a
communication step of the algorithm. This cost
only communnication steps. The requirement that and
P must be power of 2 insures that the butterfly network is properly
folded onto the P processors.
From the previous discussion, it appears that the assumptions in the beginning of this sections can be relaxed to the following ones
Finally, when temporal locality exists, the sorting method may be of some help in the inspector step of the inspector/executor scheme: sorting the indirection array may be useful for building the schedule.