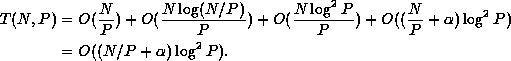Let
N be the size of the distributed array and P the number of
processors. We can derive a model for the sorting method from its
three components:
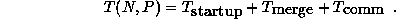
The index computation (if the target array is not block-distributed)
contributes for O(N/P) to the startup cost. The initial sorting
of local arrays contributes for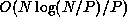 
if some fast
sequential sorting algorithm is used. The number of merge operations
is proportional to the number of parallel steps of OEMS, which is
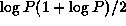and to N/P, the size of the local array. Clearly, evaluating
the communication cost is more
difficult. Independent tests on PVMe proved that the communication
time
is composed of a startup time and a part linear in the array
size. Hence, the communication time is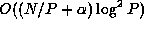 
.
Finally, we get:
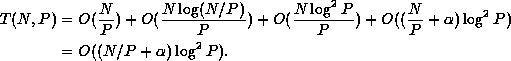
The global method basically sends all local arrays to all processors,
thus has complexity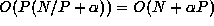 
if only
point-to-point communications are available.
Although both algorithms are asymptotically inefficient, because T(N,
P) goes to infinity for large P, the sorting methods has two
advantages. First, it goes to infinity much more slowly: the
penalizing factor is only the overhead of emulating the OEMS sorting
network; second, the
first term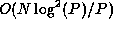 
goes to 0 for large P and can dominate
the second term in the range of feasible machines.