Despite its theoretical advantage over any global method, the algorithm described above cannot be considered for solving the irregular memory access problem without locality in compilers and run-time systems for data parallel languages, unless it allows for an efficient implementation. We now describe an implementation experiment, and a performance comparison with a commercial compiler, which shows that our method is much more efficient in practice than the global method.
Our implementation differs in one point from the theoretical model
sketched above, because we do not use a fast sequential sorting
algorithm in the initial step. The reason is that the execution time of fast sequential sorting
algorithms is highly data-dependent (quicksort is 
on
average, but 
in the worst case). In order to be sure that
our results make sense without too numerous experiments, we choose
to perform the initial local sorts by the sequential implementation of OEMS although it has sequential complexity 
.
Then the only impact of the initial data is to perform or not a swap at each
step. Taking into account the superscalar architecture of the POWER2
processor, the actual values of the indirection array only have a
slight impact on performance.
We must stress that this choice is only targeted towards
experiment, and that an end-user
targeted implementation could only display better performance.
All the measurements were performed on an IBM SP-2, with up to 64 processors available for parallel tasks and with the TB03 switch. For the sorting method, the compiler is cc with -O3 optimization level, and read_real_time timer. The message-passing library is PVMe 2.1 (PVMe is the IBM proprietary version of PVM optimized for the SP switch). Reported times are average over random initial values of the indirection array and are given in microseconds.
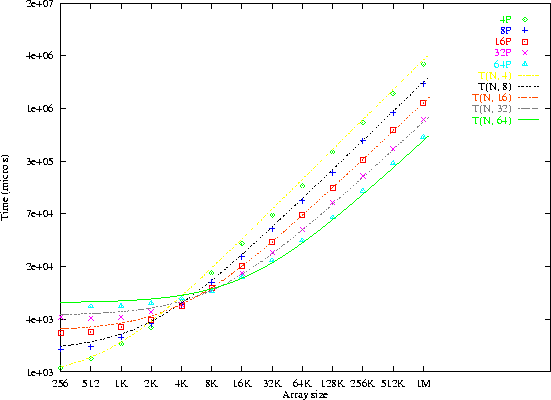
Figure 2: Execution times for the sorting method. Points are experimental
data and lines are the expected time from the T(N, P) model
Figure 2 plots the execution times of a scatter over block-distributed and identically sized arrays, for various sizes of the distributed arrays, from 128 to 1M double precision real.
The first important observation is that increasing the number of processors increases the performance if the arrays are sufficiently large. The crossover point is in the 1K to 5K range, which is moderate for a distributed array.
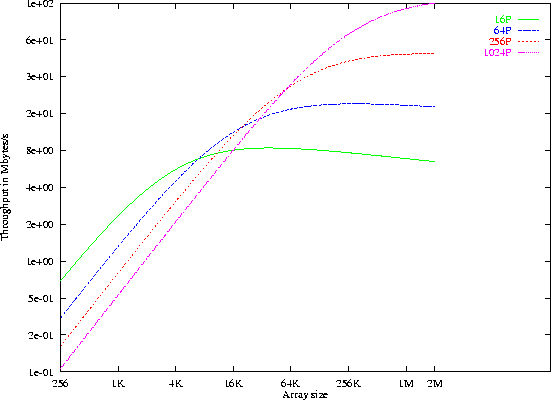
Figure 3: Throughput for the sorting method
In order to extend our results to larger
machines, the theoretical model described above can be completed with numerical
values computed by independently testing the startup, merge and
communication parts. We get
with
a = 1/30, b = 300 and c = 0.95.
Figure 2 shows that the model is very accurate. The throughput r(N, P) is the number of bytes transferred by unit time. As we considered double precision arrays, r(N, P) = 8N/T(N, P). Using the previous model, it appears that for a reasonable number of processors, the throughput has a complex behavior, but basically increases with the number of processors (fig. 3).
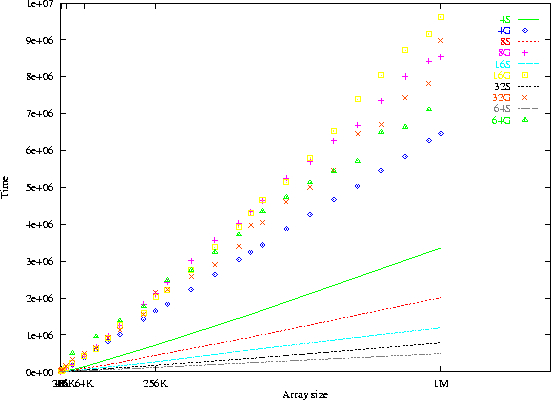
Figure 4: Comparison of execution times. Points are for the global
method and lines for the sorting method
The data-parallel scatter is a simple array assignment, written in HPF:
forall (i=1:N) A(C(i)) = B(i)where arrays A, B, C are aligned with the same template and block-distributed. The PROCESSOR geometry is known at compile-time. The compiler is xlhpf90, with -O3, -qhot and -qarch=pwr2 optimization options. The timer is the same, and is called without any hpf_serial or hpf_local interface, so as to avoid unnecessary synchronization points. Figure 4 plots the average execution times for the data-parallel scatter, and for the sorting method. Clearly, for the the global method, increasing the number of processors degrades the performance for almost all sizes of arrays . Moreover, for all configurations of processors the sorting method consistently outperforms the global method.
