Maîtriser le langage logique

La logique s’intéresse à la notion de vérité et de raisonnement. Un raisonnement est un discours qui permet d’établir la vérité d’un fait. Dans ce cours, nous nous intéressons à la logique mathématique qui s’appuie sur un langage formel pour décrire les formules, une définition rigoureuse de la notion de vérité d’un énoncé et un ensemble de règles fixé pour effectuer un raisonnement logique. Une démonstration logique ne sera donc pas un discours en langue naturel mais une suite bien précise de constructions qui obéissent à des règles du jeu définies.

Dans ce chapitre nous introduisons le langage de la logique du premier ordre, appelée aussi calcul des prédicats.

1.1 Définition du langage

On utilisera un langage formel pour écrire les propositions afin d’éviter les ambiguïtés du langage naturel ou des notations imprécises. Dans le langage naturel, le même mot peut refléter des situations logiques différentes. On le voit dans les énoncés ci-dessous avec différents sens pour le connecteur ou qui a souvent dans le langage courant un sens exhaustif (l’un des deux mais pas les deux), ou encore dans la dernière phrase dans laquelle le concept d’être une étoile représente deux réalités différents (entre l’astre et la vedette).

Un langage formel présente également moins de redondance que le langage naturel dans lequel la même situation logique peut s’exprimer de plusieurs manières différentes. Les langages formels sont donc plus simples à étudier et à représenter en machine.

1.1.1 Objets

Une formule décrit une propriété (vraie ou fausse) qui en général va parler d’objets (on appellera termes les expressions qui représentent les objets), par exemple des entiers, des figures géométriques, mais aussi des ensembles, des fonctions, des éléments dans une base de données ….

Pour décrire les objets, on introduira un langage spécifique formé de symboles qui sont juste des suites de caractères spécifiques. Chaque symbole utilisé dans le langage des objets est défini avec une arité qui est un entier naturel représentant le nombre d’arguments qu’il faut associer au symbole pour représenter un nouvel objet.

Lorsqu’un symbole est d’arité 0, on dit que c’est une constante. Cela représente donc un objet sans nécessité d’argument supplémentaire. Ce sont les objets de base. Par exemple on peut introduire 0, 1, ∅ (notation pour l’ensemble vide) comme des constantes particulières.

Un symbole d’arité 1 est dit symbole unaire. Le symbole lui-même ne représente pas un objet, par contre, si on l’associe à un terme (on dit parfois que l’on applique le symbole au terme), alors on forme ainsi un nouveau terme qui représente un objet. On peut par exemple introduire un symbole unaire sqrt pour représenter l’opération de racine carrée. On pourra alors former un nouveau terme sqrt(1). Attention le terme sqrt(1) est différent du terme 1. Dans le cas des ensembles, on peut introduire un symbole unaire P pour représenter l’ensemble des parties. Le terme P(∅) représente l’ensemble des parties de l’ensemble vide (qui est un ensemble qui contient un unique élément).

Un symbole d’arité 2 est dit symbole binaire, c’est le cas des symboles pour représenter les opérations arithmétiques +, × ou bien l’union de deux ensembles. Il faut commencer par construire deux termes avant de pouvoir les associer au symbole binaire pour construire un nouveau terme.

Définition 1 (Signature) Une signature est un ensemble de symboles F chacun associé à une arité.

Un symbole d’arité 0 est appelé constante, un symbole d’arité 1 est dit unaire, un symbole d’arité 2 est dit binaire.

Le langage des objets utilise également des variables d’objets qui sont aussi des symboles qui représentent des objets, mais contrairement aux constantes, elles ne désignent pas un objet particulier, mais sont une manière de nommer un objet arbitraire comme par exemple dans l’expression x+1.

Définition 2 (Terme) Étant donné une signature F et un ensemble X de variables, un terme t est soit une variable, soit formé d’un symbole f d’arité n et d’une suite ordonnée de n termes t₁,…,t_n. On dit alors que f est le symbole de tête et que t₁,…,t_n sont les sous-termes directs du terme t.

On note T(F,X) l’ensemble des termes sur la signature F et l’ensemble des variables X. On notera T(F) le sous-ensemble de ces termes qui ne contiennent pas de variable, appelés aussi termes clos.

La manière d’écrire le terme peut varier suivant les systèmes mais la structure du terme (variable ou symbole associé à 0, 1 ou plusieurs termes) reste la même. Si f est un symbole de fonction binaire et que t et u sont des termes, le terme obtenu avec comme symbole de tête f et comme sous-termes t et u se notera par défaut f(t,u). Pour quelques symboles spécifiques, on pourra utiliser une notation dite infixe qui consiste à placer le symbole principal entre les deux termes comme par exemple pour l’addition t+u.

Exemples de signature d’objets

1.1.2 Formules atomiques

Les formules atomiques représentent une notion qui peut être vraie ou fausse et que l’on ne peut pas décomposer sur une base logique. Il s’agit plutôt de propriétés que l’on observe plutôt que des formules logiques sur lesquelles on peut raisonner.

Parmi les formules atomiques, on distingue deux objets spéciaux : la formule notée ⊤ (aussi appelé formule vraie, ou tautologie) qui est toujours vraie et la formule ⊥ qui est toujours fausse, aussi appelée contradiction.

Les formules atomiques qui ne sont pas ⊤ ou ⊥ sont construites à partir de symboles de prédicat. Elles servent à représenter des propriétés de base des objets.

Un symbole de prédicat est juste une suite de caractères à laquelle on va pouvoir attribuer ultérieurement un sens. Comme pour les symboles d’objets, on associe à un symbole de prédicat un entier naturel que l’on appelle une arité. Cet entier correspond au nombre d’arguments représentants des objets qu’il faudra associer au symbole pour en faire une formule. On peut faire une analogie entre un symbole de prédicat et une procédure en programmation à laquelle on passe des arguments avant de pouvoir l’exécuter.

On dispose souvent (mais pas tout le temps) d’un symbole de prédicat binaire (arité 2) pour représenter l’égalité. On note de manière infixe t=u, le symbole d’égalité appliqué aux deux termes t et u.

Définition 3 (Formule atomique) Une formule atomique est soit un des symboles ⊤ ou ⊥, soit un symbole de prédicat associé à un ou plusieurs objets (le nombre d’objets attendu correspond à l’arité du prédicat).

La plupart des modélisations utilisent un symbole de prédicat binaire = qui modélise le fait que deux objets sont égaux, c’est-à-dire qu’ils vont représenter la même entité.

Exemple 1 (Egalité)
On se donne un langage dans lequel on a des constantes 0, 1, 2 et 4 ainsi qu’un symbole de fonction binaire + et un symbole de prédicat binaire =.

Les formules suivantes sont atomiques, le symbole de prédicat utilisé est l’égalité qui est un prédicat binaire (d’arité 2) : 0 = 1, 2+2 = 4, x = x, x = y
Par contre la formule 0≠1 qui sera définie comme la négation de 0=1 n’est pas une formula atomique.

Lorsqu’on modélise des systèmes d’information, l’organisation en ensembles et en tables sera représentée logiquement par des symboles de prédicat.

Exemple 2 (Systèmes d’information) Une table à n colonnes dans une base de données relationnelle peut se modéliser en logique comme un symbole de prédicat d’arité n.

La formule atomique Etudiant(Durand, Bob, 347890, 01/01/1990) correspondra à l’existence d’une entrée (Durand, Bob, 347890, 01/01/1990) dans la table ”Etudiant”.
Un système qui modélise des trajets de bus distinguera dans ses données des chaînes de caractères qui représentent indifféremment des lignes, des arrêts et des horaires. On pourra introduire trois prédicats unaires ligne, arret et horaire pour séparer les objets de la logique suivant leur catégorie. Pour modéliser une table qui tient à jour les rotations de bus avec le numéro de ligne, l’arrêt de départ, celui d’arrivée ainsi que l’horaire de départ, on peut introduire un prédicat trajet d’arité 4. La formule atomique trajet() représente le fait qu’un bus de numéro 91.06 effectue un trajet de Massy-Palaiseau gare à Christ de Saclay à 6:00.

Un symbole de prédicat est juste un nom (on dit que c’est de la syntaxe). La sémantique lui attribue un sens en lui associant une relation mathématique entre les objets modélisés. Il y a parfois un sens implicite (par exemple l’égalité ou l’ordre sur les entiers) mais d’un point de vue logique, de nombreuses interprétations sont possibles.

L’arité d’un symbole de prédicat peut être 0. Le symbole de prédicat représente alors à lui tout seul une formule vraie ou fausse. On parle alors de variable propositionnelle. On verra que c’est un cas important, car avec seulement des variables propositionnelles, la logique (que l’on appelle alors logique propositionnelle ou calcul propositionnel) devient décidable. De nombreux problèmes peuvent se modéliser en logique propositionnelle, quitte à introduire des milliers de variables propositionnelles et de formules.

Les symboles se choisissent en fonction du problème à modéliser et il y a souvent plusieurs manières de faire.

Exemple 3 (Modélisation) Si dans un problème on cherche à modéliser la situation Paul est mon ami, alors il suffit d’introduire une variable propositionnelle (qui pourra être vraie ou fausse) et qui représente le fait que Paul est (ou non) mon ami. Si par contre on veut modéliser une phrase comme «tous mes amis habitent Paris», alors il faut un symbole de prédicat unaire ami tel que ami(t) est vrai lorsque t est mon ami et un symbole de prédicat unaire paris tel que paris(t) est vrai lorsque t habite Paris, en introduisant en plus une constante Paul on peut facilement traduire la notion Paul est mon ami. Si maintenant la propriété à montrer est «les amis de mes amis sont mes amis»alors il faudra passer à un symbole de relation binaire tel que amis(t,u) est vrai si t et u sont amis et utiliser une constante self pour représenter la personne qui s’exprime.

Etant donnée une situation à représenter en logique, il peut être demandé de la modéliser et donc de trouver les bons symboles à introduire pour pouvoir représenter le problème. Dans d’autres situations, le langage peut être imposé (comme lorsque on doit utiliser l’interface d’une bibliothèque donnée) et il faudra se limiter aux symboles autorisés.

Notation infixe

La notation standard pour un symbole f d’arité au moins 1 (symbole de fonction ou de prédicat) est f(t₁,…,t_n).

Pour certains symboles binaires (d’arité 2), on utilise parfois plutôt une notation infixe, c’est-à-dire que l’on écrira t ∘ u plutôt que f(t,u). Par exemple : t + u, t × u pour des termes et t = u, t ≤ u pour des formules atomiques.

1.1.3 Formules complexes

Les formules complexes se construisent à partir des formules atomiques à l’aide de connecteurs logiques. On distingue la partie dite propositionnelle :

La quantification universelle peut se voir comme une conjonction généralisée sur tous les x possibles (il peut y en avoir une infinité, pas forcément dénombrable). La quantification existentielle peut se voir comme une disjonction généralisée, elle aussi possiblement infinie.

Exemple 4 (Formules complexes) On se place dans un langage dans lequel on a un prédicat unaire yeux-bleus. La formule atomique yeux-bleus(x) représente le fait que l’objet x a les yeux bleus. On introduit également une variable propositionnelle A.

tout le monde a les yeux bleus : ∀ x, yeux-bleus(x)
il existe une personne qui a les yeux bleus : ∃ x, yeux-bleus(x)
il existe une personne telle que si cette personne a les yeux bleus alors tout le monde a les yeux bleus : ∃ x, (yeux-bleus(x)⇒ ∀ y, yeux-bleus(y)) ¹
S’il existe une personne qui a les yeux bleus alors tout le monde a les yeux bleus : (∃ x, yeux-bleus(x))⇒ (∀ y, yeux-bleus(y)) ²
tiers exclu : A ∨ ¬ A (soit une formule est vraie, soit sa négation est vraie)
élimination des doubles négations : (¬ ¬ A) ⇒ A, (une formule dont la négation est fausse est vraie)
raisonnement par l’absurde (¬ A ⇒ A)⇒ A (si A est vrai sous l’hypothèse ¬ A alors A est vrai sans hypothèse)

Exemple 5 (Formules paramétrées) Les formules logiques permettent aussi d’énoncer des propriétés d’objets. On se place dans un langage qui contient les constantes 1 et 2, les opérations binaires + et * et le symbole d’égalité.

on peut exprimer le fait que l’entier x est impair à l’aide de la formule logique ∃ y, x=2× y+1.
Cette formule n’est pas a priori vraie ou fausse, cela dépendra de la valeur que l’on donne à x.
De même on peut exprimer le fait que l’entier x est pair à l’aide de la formule logique ∃ y, x=2× y.
A l’aide de ces définitions, on pourra exprimer la propriété qui dit qu’un entier qui n’est pas pair est impair : ∀ x, ((∀ y, ¬(x=2× y)) ⇒ (∃ y, x=2× y+1))

Notations

On pourrait ajouter le connecteur logique d’équivalence dans la définition des formules complexes. Nous utiliserons plutôt la notation A ⇔ B comme un raccourci pour la formule (A ⇒ B) ∧ (B ⇒ A).

On peut introduire plusieurs variables dans un quantificateur, par exemple : ∀ x y, P représente la formule ∀ x, ∀ y, P.

En mathématique usuelle, on utilise parfois d’autres notations logiques comme ∃! x,A pour «il existe un et un seul x qui vérifie A» ou encore ∀ x∈ E,A (la propriété A est vérifiée pour tous les objets x dans E) et ∃ x∈ E,A ( il existe un objet x dans E qui vérifie la propriété A).

Néanmoins ces notations logiques ne sont pas primitives et cachent des constructions plus complexes. L’unicité par exemple présuppose l’existence d’un symbole d’égalité qui nous permet de dire si deux termes représentent le même objet (et donc de compter). La restriction d’un quantificateur sur un ensemble demande une modélisation des ensembles et de la notion d’appartenance, de plus elle se traduit par une implication dans le cas du quantificateur universel et par une conjonction dans le cas existentiel. Les exercices 1 et 3 donnent des exemples. Ces notations de haut niveau ne feront pas partie a priori du langage logique utilisé dans ce cours.

Différentes catégories syntaxiques

Dans le langage de la logique, on distingue deux catégories syntaxiques, les termes et les formules. En particulier, il y aura des symboles de fonctions (comme 0 ou +) qui permettent de construire des termes et des symboles de prédicat pour construire les formules. La catégorie des termes (expressions qui représentent des objets) se construit à partir des données suivantes

La catégorie des formules logiques se construit à partir des symboles de prédicats

Les règles précédentes correspondent à une représentation arborescente des termes et des formules sur laquelle nous reviendrons dans la section 1.2. Lorsqu’on écrit des formules comme des suites de caractère, il est nécessaire d’introduire des parenthèses de manière à délimiter les constructions et à éviter les ambiguïtés. Cela doit être pris en compte si on écrit un programme qui “lit” des formules logiques entrées de manière séquentielle par l’utilisateur pour les représenter ensuite en machine comme des arbres.

L’accumulation des parenthèses alourdit parfois les notations et des conventions permettent d’en éliminer un grand nombre. On choisit souvent une présentation ambigüe de la syntaxe, sans mettre systématiquement de parenthèses autour des opérateurs mais en ajoutant la possibilité de parenthéser n’importe quelle sous-expression sans en altérer le sens.

Si les termes n’utilisent que la notation préfixe pour les symboles alors il n’y a pas besoin de parenthèses additionnelles au niveau des termes. Par contre si certains symboles utilisent une notation infixe, il faudra aussi autoriser des termes parenthésés, par exemple pour lever une possible ambiguïté sur un terme comme x−y−z qui pourrait se lire comme (x−y)−z ou comme x−(y−z).

Calcul des prédicats et calcul propositionnel.

On appelle logique du premier ordre (ou calcul des prédicats) le langage logique défini par une signature (symboles de fonctions et de prédicats) et qui n’utilise que les connecteurs logiques et les quantificateurs sur les variables de termes tels que définis précédemment.

Le calcul propositionnel (aussi appelé logique propositionnelle) est un cas particulier dans lequel la signature est réduite à des symboles de prédicats d’arité 0 (variables propositionnelles) et dans lequel on n’utilise pas de quantificateurs.

Il existe beaucoup d’autres logiques comme des logiques multi-sortes dans lesquelles les termes sont séparés dans des classes différentes (à la manière des types dans les langages de programmation) ou encore des logiques d’ordre supérieur dans lesquels on peut aussi quantifier sur les formules ou encore des logiques temporelles qui intègrent des quantificateurs spéciaux pour raisonner sur le comportement de systèmes. La logique du premier ordre est le socle de référence de toutes ces logiques et l’outil de base pour le raisonnement mathématiques.

1.1.4 Traduire des énoncés en formule logique

On suppose que l’on se place dans un langage avec les prédicats amis(x,y) qui représente le fait que x et y sont amis et une constante self qui représente l’individu qui s’exprime. On cherche à traduire en une formule logique la phrase «les amis de mes amis sont mes amis». On peut procéder par étape

Exercice 1 On ajoute au langage précédent le prédicat joue(x,y) qui représente le fait que x joue avec y et un prédicat d’égalité. Traduire en formules logiques les expressions suivantes :

je ne joue qu’avec mes amis
tout le monde a un ami
je n’ai pas d’ami avec qui jouer
j’ai au moins deux amis (on utilisera la relation d’égalité)

Exercice 2 On se place dans un langage qui contient un symbole de fonction binaire + qui représente l’addition, un symbole de prédicat unaire pair tel que pair(x) exprime que l’entier x est pair.

Écrire la formule qui dit que la somme de deux entiers pairs est un entier pair. On fera attention à bien distinguer les expressions qui représentent des objets (termes) de celles qui représentent des énoncés (formules).

Exercice 3 En logique du premier ordre, lorsque l’on écrit la formule ∀ x,P ou ∃ x,P on englobe tous les objets possibles (sans préciser dans quel univers se placent ces objets). En mathématiques, la quantification est restreinte à un ensemble particulier. On écrira par exemple dans le cas des entiers naturels ∀ x∈ℕ,P ou ∃ x∈ℕ,P.

En utilisant un symbole de prédicat unaire N, tel que N(x) représente le fait que x∈ℕ, donner des formules de la logique du premier ordre qui représentent les deux quantifications ensemblistes ∀ x∈ℕ,P et ∃ x∈ℕ,P.

Compétences 1

Connaître les notions de signature et arité.
Distinguer les termes et les formules, et parmi les formules celles qui sont atomiques.
Reconnaître les termes et les formules syntaxiquement bien formés.
Comprendre le sens intuitif des connecteurs propositionnels et quantificateurs logiques.
Savoir lire une formule logique et traduire une propriété exprimée en langue naturelle en utilisant le langage de la logique.

1.2 Structure des formules

1.2.1 Représentation des formules comme des arbres

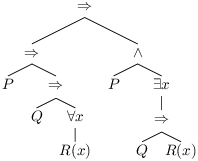
Une formule peut se voir comme un arbre dont les nœuds internes sont les connecteurs logiques (les connecteurs propositionnels sont binaires, sauf la négation qui est unaire) et les quantificateurs ∀ x, ∃ x qui sont des nœuds internes unaires. Les feuilles de l’arbre sont les formules atomiques.

On suppose que P et Q sont des variables propositionnelles et que R est un symbole de prédicat unaire. On peut dessiner sous forme d’arbre la formule (P ⇒ (Q ⇒ (∀ x, R(x)))) ⇒ (P ∧ (∃ x, (Q ⇒ R(x)))) :

Cette représentation arborescente pourra être utilisée si on veut représenter les formules en machine. C’est aussi elle qui va nous servir pour construire des fonctions sur les formules et aussi pour raisonner sur les formules.

Exercice 4 Donner la forme arborescente de la formule (∀ x, (R(x) ⇒ Q)) ⇒ (¬ Q ⇒ ¬ (∃ x, R(x))).

1.2.2 Notations, règles de parenthésage

La définition des formules complexes correspond à une méthode de construction des formules à partir des formules atomiques. Pour lever toute ambiguïté, on peut mettre des parenthèses autour de chaque formule non atomique, néanmoins cela alourdit considérablement l’écriture et peut nuire à la lisibilité. Si on supprime les parenthèses et que l’on écrit simplement P ∧ Q ∨ R il y a une ambiguïté: cette formule peut se construire de deux manières différentes suivant si on utilise d’abord la règle pour la disjonction puis la conjonction ou bien dans l’autre sens. Pour lever cette ambiguïté, on utilise des parenthèses et on pourra écrire P ∧ (Q ∨ R) ou bien (P ∧ Q) ∨ R. Les parenthèses sont importantes car les deux formules ne sont pas vraies en même temps (prendre P faux et Q et R vrai).

Comme pour les formules arithmétiques, il y a des règles de précédence pour les connecteurs logiques qui évitent l’utilisation systématique des parenthèses. La précédence de ¬ est la plus forte, vient ensuite la conjonction ∧ puis la disjonction ∨ et finalement l’implication ⇒.

Dire que ¬ a une précédence plus forte que ∧ signifie que la formule ¬ P ∧ Q doit se parenthéser en (¬ P) ∧ Q et non pas en ¬ (P ∧ Q). De même dire que ∧ a une précédence plus forte que ⇒ signifie que P ⇒ Q ∧ R se parenthèse comme P ⇒ (Q ∧ R) et non pas (P ⇒ Q) ∧ R. On commence par mettre les parenthèses autour du connecteur dont la précédence est la plus forte.

Les connecteurs ∧, ∨ et ⇒ associent à droite, ce qui signifie que la formule P⇒ Q⇒ R se parenthèse en P⇒ (Q⇒ R) et non pas (P⇒ Q)⇒ R.

L’ordre des parenthèses ne change pas le sens des formules pour les connecteurs ∧ et ∨ qui sont associatifs. Par contre, dans le cas de l’implication, les formules P⇒ (Q⇒ R) et (P⇒ Q)⇒ R ne disent pas du tout la même chose, il faut donc être très attentif à ne pas se tromper.

Exemple 6 P ∧ R ∧ ¬ Q ⇒ P ∨ Q ∧ R représente donc la même formule que (P ∧ (R ∧ (¬ Q))) ⇒ (P ∨ (Q ∧ R)).

Exercice 5 Pour chacune des formules suivantes, donner sa représentation sous forme d’arbre ainsi qu’une forme avec des parenthèses sans changer le sens:

(P ⇒ Q ⇒ R) ⇒ P ∧ Q ⇒ R
(P ⇒ Q) ⇒ ¬ Q ⇒ ¬ P

Précédence des quantificateurs

Les quantificateurs ∀ et ∃ ont une précédence plus faible que les autres opérateurs. Leur portée s’étend donc aussi loin que possible.

Exemple 7 ∀ x, P ⇒ Q représente ∀ x, (P ⇒ Q) et non pas (∀ x, P) ⇒ Q.

Exercice 6 Exprimer sous une forme logique l’adage suivant: “Tout ce qui ne nous tue pas nous rend plus fort”. On se donne comme symbole de prédicat de base Tue(x) et Fort(x). Représenter la formule sous forme d’arbre. Écrire la formule avec toutes les parenthèses puis avec le minimum de parenthèses.

1.2.3 Variables libres, liées

Dans les formules ∀ x, P et ∃ x, P, la variable x est dite liée (on dit aussi muette), en effet les occurrences de x sont reliées au quantificateur correspondant et on peut changer le nom de manière cohérente dans P et le quantificateur sans changer le sens de la formule:
∀ x, ∃ y, x < y exprime la même propriété que ∀ t, ∃ u, t < u. Une variable x qui apparaît dans une formule P mais qui n’est pas dans une sous-expression de la forme ∀ x, Q ou ∃ x, Q est dite libre. Par exemple dans la formule ∃ y, x < y, la variable x est libre et y est liée. Cette formule représente le fait que “Il existe un nombre plus grand que x”.

En langage courant, le plus souvent, on n’introduit pas de nom explicite pour les variables liées, comme dans les exemples suivants :

Définition 1 (Variables libres, Vl(P)) Soit une formule P et x une variable. On dit que x est libre dans la formule P et on écrira x ∈ Vl(P) si:

P est une formule atomique R(t₁,…,t_n) et x apparaît dans l’un des termes t_i;
P est une négation ¬ A et x ∈ Vl(A);
P est une formule composée A∧ B, A∨ B, A⇒ B et x ∈ Vl(A) ou x ∈ Vl(B);
P est une formule quantifiée ∀ y,A ou ∃ y,A avec x≠y et x ∈ Vl(A).

Une variable peut à la fois apparaître en position libre et en position liée, ou bien apparaître liée dans plusieurs quantificateurs comme y dans la formule 0<x× y ∨ (∃ y, x < y) ∧ (∃ y, y+y < x). Cependant ces trois positions ne représentent pas la même chose car on peut toujours choisir un nom nouveau pour les variables liées. La formule pourra s’écrire: 0<x× y ∨ (∃ y₁, x < y₁) ∧ (∃ y₂, y₂+y₂ < x).

Exercice 7 Donner les variables libres de la formule : ∀ b, b > 0 ⇒ ∃ q, ∃ r, a = b × q + r ∧ r < b.

Les variables libres représentent des paramètres de la formule par exemple dans la formule ∃ y, x=2× y, la variable x est libre, la formule représente la notion “x est pair”, qui dépend de x. Cette formule est vraie ou fausse en fonction de la valeur de la variable x. On peut faire une analogie avec une variable globale d’un programme qui devra avoir une valeur pour permettre une exécution.

Une variable libre peut être remplacée par un terme plus complexe, on parle de substitution, par exemple

Attention au phénomène de capture lorsqu’on substitue une variable par un terme. Supposons que l’on veuille écrire la formule “3× y est pair” :

On notera P[x← t] la formule obtenue en remplaçant dans P les occurrences libres de la variable x par le terme t, après avoir si nécessaire renommé les variables liées de P afin d’éviter de capturer les variables qui apparaissent dans t. La définition précise de la substitution dans les formules sera donnée plus tard (définition 3).

Définition 2 (Terme clos, formule close)

Un terme qui ne contient pas de variables est appelé terme clos.
Une formule qui ne contient pas de variable libre est appelée formule close.

Compétences 2

Connaître les règles de précédence sur les connecteurs et les quantificateurs de la logique.
Savoir représenter une formule sous forme d’arbre.
Reconnaître les variables libres et les variables liées d’une formule logique.
Connaître la définition de terme clos et formule close.

1.3 Formule vraie

Il y a deux valeurs de vérité vrai et faux. On les représente par les éléments de l’ensemble B={V,F} des booléens. L’élément V correspond à vrai et F à faux. On utilise parfois les entiers {1,0} à la place, mais il est préférable de ne pas confondre valeur de vérité et valeur entière, d’où le choix de notations spécifiques.

Pour définir quand une formule quelconque est vraie, il faut se placer dans un modèle (on parle aussi d’interprétation) qui explicite de quels objets on parle et également pour chaque symbole de prédicat (propriété atomique), nous dit pour quels objets il est vérifié.

Par exemple, dans le modèle usuel des mathématiques 2 ≤ 4 est vrai mais 0=1 est faux. L’énoncé «Anne est l’amie de Bob» peut être vrai dans certaines situations et faux dans d’autres. L’énoncé «Tout le monde a les yeux bleus» sera vrai ou faux en fonction de notre interprétation de «tout le monde», suivant si on se restreint a une famille donnée ou bien si on considère l’ensemble de la population française.

1.3.1 Le cas propositionnel

Une formule logique complexe contient des connecteurs logiques qui ont un sens précis.

La formule atomique ⊥ est toujours fausse et la formule atomique ⊤ est toujours vraie.

Les tables suivantes rappellent les valeurs de vérité des connecteurs propositionnels en fonction des valeurs de vérité des composants de la formule.

Pour savoir si une formule propositionnelle est vraie, il “suffit” de la décomposer pour se ramener à la vérité des formules atomiques qui la composent.

Si une formule propositionnelle ne contient pas de variables propositionnelles ni de symboles de prédicats, alors on peut calculer sa valeur de vérité en utilisant les tables ci-dessus.

Par exemple ((⊥⇒ ⊥) ⇒ ⊥) ⇒⊥ est une formule propositionnelle qui est toujours vraie.

Les formules sans symboles de prédicat ne sont pas très intéressantes à étudier. On va donc se placer dans le cas d’une formule propositionnelle (pas de quantificateur) qui ne contient comme symboles de prédicat que des variables propositionnelles (symbole d’arité 0, sans argument).

Une variable propositionnelle dans une formule peut prendre soit la valeur vrai, soit la valeur faux. C’est une inconnue du problème. Une formule propositionnelle contient un nombre fini de variables propositionnelles que l’on note X₁,…, X_n. Chacune peut prendre comme valeur soit vrai soit faux. Il y a donc en tout 2ⁿ possibilités. Chaque choix correspond à une interprétation différente. Si on fixe une interprétation, alors on peut calculer la valeur de vérité de la formule dans cette interprétation en utilisant les tables ci-dessus.

Définition 1 (Table de vérité) Soit une formule P qui contient les variables propositionnelles X₁,…, X_n. La table de vérité de la formule P est un tableau à n+1 colonnes étiquetées par X₁,…, X_n,P.

Chaque ligne correspond à une interprétation différente de X₁,…, X_n et contient dans la colonne P, la valeur de la formule P dans cette interprétation.

La table de vérité contient a priori 2ⁿ lignes (une par interprétation). Cependant la valeur de vérité d’une formule ne dépend parfois que de la valeur d’une ou deux variables propositionnelles, on s’autorisera alors à n’écrire qu’une seule ligne, en laissant les valeurs des autres variables indéterminées (et donc cette ligne représentera plusieurs interprétations pour lesquelles la valeur de P est la même).

Exemple 8 Soit la formule P définie par (A⇒ B⇒ C) ⇒ (A⇒ B)⇒ A⇒ C avec A, B et C des variables propositionnelles.

Avant de construire la table de vérité, il est préférable de parenthéser la formule pour lever toute ambiguïté, ici on obtient (A⇒ (B⇒ C)) ⇒ ((A⇒ B)⇒ (A⇒ C)).

La formule P a trois variables propositionnelles A, B et C, et donc la table de vérité a 8 lignes que l’on peut énumérer avant de calculer la valeur de la formule sur chaque ligne.

A	B	C	P
V	V	V	?
V	V	F	?
V	F	V	?
V	F	F	?
F	V	V	?
F	V	F	?
F	F	V	?
F	F	F	?

Plutôt que cette approche « brute-force » qui est propice aux erreurs de calcul, on peut procéder de manière plus subtile en traitant en priorité les cas pour lesquels le calcul de la formule est immédiat (par exemple une conjonction est fausse si l’un des membres est faux, quelle que soit la valeur de l’autre membres).

Dans notre exemple la formule est vraie trivialement si C est vrai. On peut donc faire une première ligne

A	B	C	P
*	*	V	V

Cette ligne couvre 4 interprétations différentes (toutes les valeurs combinées possibles pour A et B). Les autres interprétations à considérer sont celles où C a la valeur faux. La formule P est aussi vraie lorsque A est faux car alors A ⇒ C est toujours vrai. On peut donc compléter la table de vérité.

A	B	C	P
*	*	V	V
F	*	F	V

Cette ligne ne couvre que deux cas supplémentaires (puisque les cas avec C vrai ont déjà été comptés). Il ne reste donc que deux interprétations à considérer dans lesquelles A est vraie et C est faux. Si B est faux alors A⇒ B est faux et donc P est vrai et si B est vrai alors B ⇒ C est faux donc A⇒ (B ⇒ C) est faux et donc P est vrai. Ce qui donne au final la table.

A	B	C	P
*	*	V	V
F	*	F	V
V	V	F	V
V	F	F	V

Validité, satisfiabilité.

On va s’intéresser à savoir si une formule est vraie pour toutes les interprétations possibles de ces prédicats (pour tous les modèles). Si c’est le cas on dira que la formule est valide ou encore que c’est une tautologie. Si la formule est vraie pour certaines interprétations, on dit que la formule est satisfiable, si elle est fausse dans toutes les interprétations alors elle est dite insatisfiable.

La terminologie satisfiable est un anglicisme couramment utilisé, on trouvera également dans les livres les qualificatif de formule satisfaisable ou insatisfaisable qui correspondent aux mêmes définitions.

Attention insatisfiable est la négation de satisfiable, mais ne pas être valide (au moins une interprétation rend fausse la formule) ne signifie pas être insatisfiable (toutes les interprétations rendent fausses la formule). Une formule valide (toutes les interprétations rendent vraie la formule) est a fortiori satisfiable (au moins une interprétation rend vraie la formule), une formule non valide (au moins une interprétation rend la formule fausse) peut être satisfiable (une autre interprétation rend vraie la formule) ou insatisfiable (la formule est tout le temps fausse).

Il y a cependant un lien direct entre validité et satisfiabilité grâce à l’opération de négation sur les formules. En effet pour toute formule P (propositionnelle ou non), La formule P est valide si et seulement si la formule ¬ P est insatisfiable. Savoir résoudre un des problèmes est donc équivalent à savoir résoudre l’autre.

Exemple 9 Soit P et Q deux variables propositionnelles.

¬ (P ∧ Q) ⇒ (¬ P ∨ ¬ Q) est une tautologie (formule valide)
¬ (P ∧ Q) ⇒ (¬ P ∨ Q) est vrai lorsque Q est vrai et lorsque P est faux mais est faux lorsque P est vrai et Q est faux (formule satisfiable).
¬ P ∧ P n’est jamais vérifié (formule insatisfiable).

Exercice 8 Les formules suivantes sont-elles valides ?

((P ⇒ Q) ⇒ P) ⇒ P
(¬ P ⇒ P) ⇒ P

Résoudre des problèmes avec la logique.

Le calcul propositionnel permet de modéliser et de résoudre des problèmes. En plus de pouvoir décider si une formule est valide, on peut également répondre à la question pour quelles valeurs des formules atomiques la propriété sera-t-elle vérifiée ? ou bien à la question combien y-a-t-il de solutions différentes ?

Exercice 9 (Enigme du tigre et de la princesse) Des prisonniers sont soumis à un test qui peut se résoudre en utilisant la logique. Ils doivent choisir entre deux portes derrière lesquelles il peut y avoir soit une princesse soit un tigre. S’ils ouvrent une porte derrière laquelle il y a un tigre, ils sont dévorés.

Des inscriptions sur les portes guident leur choix:

La porte 1 comporte la mention “Il y a une princesse derrière cette porte et un tigre derrière l’autre”, la porte 2 comporte la mention “Il y a une princesse derrière une des portes et un tigre derrière l’autre”, on sait de plus qu’une seule de ces inscriptions est vraie.

On introduit les variables propositionnelles P₁ (resp. P₂) pour représenter la présence d’une princesse derrière la porte 1 (resp. la porte 2).

Donner les formules propositionnelles représentant le problème. Quelle porte est-il préférable d’ouvrir ?

1.3.2 Formule avec quantificateurs

Le sens commun de la formule ∀ x,P est que P doit être vrai pour tous les x mais cela ne peut avoir un sens que si on explique ce que représente x.

Avant de pouvoir dire quelle est la valeur de vérité de ∀ x,P, il faut donc préciser notre interprétation des symboles. S’il y a des quantificateurs, c’est qu’il y a des objets et donc il faut préciser de quels objets on parle. On se donne donc un ensemble, appelé domaine de l’interprétation (on dira aussi plus simplement domaine) qui représente l’univers auquel appartiennent nos objets. Cet ensemble doit être non vide. On fait correspondre à chaque constante, un élément de notre domaine. Deux constantes qui ont des noms différents dans la logique peuvent parfaitement correspondre à la même valeur dans le domaine. A chaque symbole de fonction de la logique, va correspondre une fonction sur le domaine. Pour faire un parallèle avec la programmation, les symboles utilisés de la logique correspondent à l’interface d’un module à partir duquel on peut construire de nouveaux programmes alors que l’interprétation va correspondre à l’implémentation du module qui va permettre d’exécuter les programmes. Le comportement de ces programmes peut complètement changer en fonction de l’implémentation du module.

Une formule atomique P(t₁,…,t_n) représente une vérité qui dépend évidemment de la valeur des arguments t₁,…,t_n. On peut choisir l’interprétation de P parmi toutes les relations n-aires sur le domaine de l’interprétation.

Si on a un prédicat unaire comme yeux-bleus l’interprétation revient à choisir le sous-ensemble des individus qui ont les yeux bleus. Si on a une relation binaire comme amis ou ≤, l’interprétation peut se représenter comme un graphe orienté dont les sommets sont les éléments du domaine et dans lequel une arête de s à t sera présente lorsque la relation est vraie entre s et t.

Même si la formule ne contient qu’un symbole de prédicat, si le domaine est infini, le nombre d’interprétations possibles est lui-même infini et donc on ne peut plus faire une table de vérité qui énumère toutes les interprétations.

Par contre si on exhibe une interprétation qui rend vraie la formule, on sait qu’elle est satisfiable et si on trouver un contre-exemple (une interprétation qui rend fausse la formule) alors on sait qu’elle n’est pas valide.

Nous verrons dans les chapitres ?? et ?? des méthodes pour simplifier la recherche d’un modèle.

Vérité d’une formule quantifiée sans variable libre.

La vérité d’une formule sans variable libre mais avec des quantificateurs du premier ordre dépend en général de l’exploration de la vérité d’un ensemble infini de formules (obtenues en interprétant les variables par des objets arbitraires).

Exercice 10 Les formules suivantes sont-elles vraies pour toute interprétation du prédicat P?

(∀ x, P(x)) ⇒ ∃ x, P(x)
¬(∀ x, P(x)) ⇒ ∃ x, ¬ P(x)

Compétences 3

Savoir construire la table de vérité d’une formule propositionnelle (prérequis).
Savoir utiliser la logique propositionnelle pour modéliser et résoudre des problèmes simples.
Comprendre intuitivement la notion d’interprétation et de modèle (sera approfondi au chapitre ??).

1.4 Théories et modélisation

Une formule est un élément de syntaxe qui utilise des symboles qui peuvent avoir de nombreuses interprétations différentes.

Si au contraire on s’intéresse à certaines opérations et certaines propriétés d’un univers particulier, on peut modéliser cet univers en introduisant un ensemble de symboles et un ensemble d’énoncés A tel que notre univers corresponde à un modèle qui rend vraies toutes les formules de A.

On pourra alors travailler au niveau de la logique à partir de cet ensemble d’axiomes et en déduire des propriétés de l’univers qui nous intéresse.

1.4.1 Définitions autour des théories

Les mathématiciens se sont intéressés depuis l’antiquité à trouver des présentations axiomatiques de théories.

Axiomes pour la géométrie.

Par exemple Euclide a formalisé un ensemble d’axiomes pour la géométrie. Dans sa représentation, il choisit comme primitives les notions de points, de segment, de droite, de demi-droite et de cercle et les relie par des axiomes. Le logicien Hilbert a proposé une formulation alternative. Si on ne s’intéresse qu’à la géométrie planaire et la notion de point et de droite ainsi qu’à la relation d’incidence (un point appartient à une droite), les axiomes de Hilbert sont les suivants :

Pour formaliser cette théorie en logique du premier ordre, il nous faut des prédicats unaires P et D pour représenter respectivement les points et les droites et deux prédicats binaires (notés de manière infixe) : ∈ pour la propriété pour un point d’être sur une droite et = pour l’égalité (afin de pouvoir traduire la propriété d’unicité). Le premier axiome ci-dessus se traduit par la formule

Pour une modélisation complète de la géométrie euclidienne, Hilbert introduit d’autres notions primitives pour modéliser les distances. Une relation ternaire entre les points représente le fait qu’un point est entre deux autres. Ce qui permet d’introduire le notion de segment AB (les points situés entre les points A et B). Les notions de demi-droite, d’angle et de triangle sont aussi dérivés. Les relations de congruence sont introduites entre segments, angles et triangles pour modéliser les notions de distance et le fait que les figures géométriques se “déplacent” dans l’espace sans changer de forme.

Axiomes pour les groupes.

La théorie des groupes est une généralisation du modèle des entiers relatifs : on se donne une constante 0, une opération binaire +, une opération unaire − et un prédicat binaire d’égalité. On suppose que ces opérateurs vérifient un certain nombre de propriétés logiques

et on en déduit divers conséquences qui seront vraies pour les entiers relatifs mais aussi pour toutes les autres structures de groupe.

Définition 1 (Théorie) Une théorie est définie par un ensemble de symboles de fonctions et de prédicats (la signature de la théorie) et un ensemble de formules closes (sans variables libres) construites sur ce langage, appelés les axiomes de la théorie.

Un modèle d’une théorie est donné par une interprétation de la signature (c’est-à-dire un domaine correspondant à l’ensemble dans lequel on interprète les objets et des fonctions et relations sur ce domaine) telle que, dans cette interprétation, tous les axiomes ont pour valeur vraie.

Soit une théorie définie par un ensemble A d’axiomes. Au lieu de s’intéresser à la validité d’une formule, on va se poser la question est-ce que la formule est vraie dans tous les modèles de la théorie ? ou encore est-ce qu’on peut par un raisonnement qui suppose vrais tous les axiomes de la théorie, déduire cette propriété.

Si une formule P est vraie dans tous les modèles d’une théorie, on dit que la formule est vraie dans la théorie A ou encore qu’elle est conséquence des axiomes A.

Une théorie peut ne pas avoir de modèle, auquel cas on dit que la théorie est incohérente. Dans une théorie incohérente, même la formule ⊥ est vraie!

La théorie A est dite complète si pour toute formule P soit P est vraie dans la théorie, soit ¬ P est vraie dans la théorie.

La plupart des théories ne sont pas complètes. Si on pense à la théorie des groupes et que l’on regarde la formule qui dit que le groupe est commutatif (∀ x y, x+y=y+x) alors la théorie ne permet de prouver ni cette formule ni sa négation puisqu’il existe à la fois des groupes commutatifs et des groupes non-commutatifs.

Pour faire des mathématiques, on aimerait pouvoir définir un ensemble d’axiomes qui nous permette de capturer avec précision et rigueur ce qui est vrai ou faux.

Le théorème d’incomplétude de Gödel nous dit que toute théorie (dont on peut reconnaitre les axiomes) qui contient l’arithmétique est forcément incomplète et que quelques soient les axiomes que l’on ajoute la théorie restera incomplète à moins de devenir incohérente.

Une théorie est décidable, si on sait, pour toute formule P, décider si P est ou non une conséquence des axiomes. La théorie vide n’est pas décidable. La théorie de l’arithmétique linéaire (sans multiplication) est décidable ainsi que la théorie des réels.

1.4.2 Exemples de théories

Égalité

Une théorie importante est celle de l’égalité. Elle contient un symbole de prédicat binaire = qui sera noté de manière infixe. Les axiomes nécessaires sont les suivants.

Définition 2 (Théorie de l’égalité) Le théorie de l’égalité est donnée par les axiomes qui expriment que c’est une relation d’équivalence.

réflexivité : ∀ x, x=x
symétrie : ∀ x y, x=y⇒ y=x
transitivité : ∀ x y z, x=y⇒ y=z⇒ x=z

Pour chaque symbole de fonction f n-aire on ajoute un axiome qui exprime le fait que c’est une congruence

∀ x₁… x_n y₁… y_n, x₁=y₁∧…∧ x_n=y_n ⇒ f(x₁,…, x_n)=f(y₁,…, y_n)

et pour chaque symbole de prédicat P n-aire on ajoute un axiome qui exprime le fait que la propriété est stable par égalité :

∀ x₁… x_n y₁… y_n, x₁=y₁∧…∧ x_n=y_n ⇒ P(x₁,…, x_n)⇒ P(y₁,…, y_n)

Les axiomes de congruence sont importants en effet le symbole d’égalité peut en logique s’interpréter de manière très variée par n’importe quelle relation d’équivalence (réflexive, transitive et symétrique) de même pour l’interprétation des fonctions et des prédicats qui peuvent ne pas vérifier les propriétés de congruence.

Supposons que l’on veuille modéliser les rationnels, on pourrait introduire des symboles de fonction pour le dénominateur et le numérateur. Néanmoins la fonction dénominateur n’est pas une congruence (avec l’égalité usuelle sur les rationnels) en effet on a 1/2=2/4 mais 2≠4. Il faudra donc soit se passer des fonctions d’accès au numérateur et au dénominateur, soit distinguer une égalité de représentation dans laquelle deux rationnels sont égaux s’ils ont même numérateur et même dénominateur et donc 1/2≠2/4 et introduire une autre relation d’équivalence =_ℚ pour lier des fractions qui représentent le même rationnel. Ces considérations sont très semblables à ce que l’on rencontre en programmation. Si les langages de programmation fournissent une notion d’égalité générique, elle correspondra à une égalité des représentations des objets et il est laissé à l’usager le soin d’introduire des égalités plus larges en fonction des interprétations souhaitées.

La plupart des théories vont contenir un symbole d’égalité et donc inclure ces axiomes. On utilisera plus simplement la notation t≠u pour représenter la formule ¬(t=u).

Arithmétique

Définition 3 (Théorie arithmétique de Peano (PA)) Le langage est composé de la constante 0 du symbole de fonction unaire S et des symboles binaires + et × ainsi que du symbole de prédicat d’égalité.

Les sept axiomes suivants constituent ce que l’on appelle l’arithmétique élémentaire. Cette théorie est notée PA₀.

∀ x, S(x)≠0
∀ x, x=0∨ ∃ y, x=S(y) (inutile en présence de récurrence)
∀ x y, S(x)=S(y)⇒ x=y
∀ x, x+0=x
∀ x y, x+S(y)=S(x+y)
∀ x, x× 0=0
∀ x y, x× S(y)=(x× y)+x

La théorie PA₀ n’est pas suffisante pour prouver une propriété comme la symétrie de l’addition.

Pour obtenir l’arithmétique de Peano, on lui ajoute une infinité d’axiomes pour le schéma de preuve par récurrence. Pour chaque formule P ayant comme variables libres x₁,…,x_n,x, on aura comme axiome la formule

∀ x₁… x_n,P[x← 0] ⇒ (∀ x, P⇒ P[x← S(x)]) ⇒ ∀ x,P

On rappelle que P[x← t] représente la formule obtenue en remplaçant dans la formule P toutes les occurrences libres de la variable x par le terme t.

A tout entier n∈ℕ, on peut associer un terme de l’arithmétique de Peano Sⁿ(0) que l’on notera ñ.

On peut se demander pourquoi choisir l’addition et la multiplication et pas d’autres fonctions. En fait ces deux opérations permettent de représenter logiquement toutes les autres fonctions calculables sur les entiers sous la forme de relation. Par exemple, si on veut la soustraction, on pourra définir le fait que z représente la différence entre x et y par la formule z+y=x. On peut aussi représenter les opérations de division euclidienne et de reste modulo qui permettent de faire des codages pour des couples et des suites d’entiers.

Exercice 11 On définit la propriété t ≤ u =^def ∃ n, n+t=u. Montrer que les propriétés de base de l’ordre sur les entiers sont vraies dans la théorie de l’arithmétique. Pour la transitivité, on pourra utiliser sans la démontrer la propriété d’associativité de l’addition.

∀ x, 0 ≤ x
∀ x y, x ≤ y ⇔ S(x) ≤ S(y)
transitivité : ∀ x y z, x ≤ y ⇒ y ≤ z ⇒ x ≤ z

Exercice 12

Définir par une formule logique contenant trois variables libres x, y et d le fait que d est le résultat de la division entière de x par y. On notera div(x,y,d) cette formule.
Définir par une autre formule logique contenant trois variables libres x, y et r le fait que r est le reste modulo de la division entière de x par y.
Que pensez-vous de la valeur de vérité de la formule div(x,0,d) dans laquelle on a remplacé y par 0 ?
Si la division entière est représentée par une fonction à deux arguments, on peut écrire une propriété comme (x/y)/z=x/(y× z). Exprimer le même résultat en utilisant le prédicat div à trois arguments.

Modélisation en logique propositionnelle

Si on se place dans le fragment propositionnel (pas de quantificateurs) alors on peut savoir si une formule est satisfiable, valide ou non. Les SAT-solvers sont des outils qui permettent de traiter des problèmes propositionnels. L’idée est d’avoir des variables pour des propositions atomiques qui peuvent valoir vrai ou faux, puis de décrire un problème sous la forme de contraintes sur ces variables exprimées comme des formules propositionnelles. L’outil détermine s’il existe une manière d’affecter une valeur vrai ou faux à chaque variable propositionnelle qui rende le problème vrai.

Exemple 10 On peut modéliser un problème de Sudoku sous une forme propositionnelle. Pour cela on introduit 9³=729 variables X_ijk pour i,j,k∈ [1,9]. L’interprétation est que X_ijk est vrai si le chiffre k est sur la i-ème ligne et la j-ème colonne. On peut ensuite exprimer les contraintes :

Au plus un seul chiffre k par case (i,j): Par exemple pour indique que sur la case (1,1) il n’y a pas plusieurs chiffres on va dire que s’il y a un 1 alors il ne peut y avoir ni un 2, ni un 3, etc c’est-à-dire
X₁₁₁ ⇒ ¬ X₁₁₂∧¬ X₁₁₃ ∧¬ X₁₁₄∧¬ X₁₁₅∧¬ X₁₁₆∧¬ X₁₁₇∧¬ X₁₁₈∧¬ X₁₁₉

On écrit cette formule de manière plus synthétique : X₁₁₁ ⇒ ∧_l≠1 ¬ X_11l.
Au final il faudra écrire 9³ formules pour toutes les valeurs de i,j,k∈ [1,9] de la forme :
X_ijk ⇒ ∧_l≠k ¬ X_ijl

En utilisant le fait que la formule A⇒ (B∧ C) est équivalente à (A⇒ B)∧ (A⇒ C) et que A⇒ B est équivalent à ¬ A∨ B on peut transformer l’ensemble de formules précédents en des formules plus symétriques ¬ X_ijk∨¬ X_ijl pour tout i,j∈[1,9] et pour toutes les paires d’éléments k≠l. On a au total 9× 9× 9× 4 formules.
Chaque chiffre k apparaît sur chaque ligne i au moins dans une colonne j. La formule qui dit que le chiffre 1 apparaît au moins une fois sur la première ligne s’écrit :
X₁₁₁ ∨ X₁₂₁∨ X₁₃₁ ∨ X₁₄₁∨ X₁₅₁ ∨ X₁₆₁∨ X₁₇₁ ∨ X₁₈₁∨ X₁₉₁

que l’on écrit de manière synthétique ∨_j=1..9 X_1j1 et au final il faudra écrire 9² formules (une pour chaque ligne i et pour chaque chiffre k) de la forme ∨_j=1..9 X_ijk
Chaque chiffre k apparaît au plus une fois sur chaque ligne i (s’il est dans la colonne j, il n’est pas dans une autre colonne) :
La formule qui dit que le chiffre 1 apparaît au plus une fois sur la première ligne et la première colonne alors il n’apparaît pas dans une autre colonne s’écrit :
X₁₁₁ ⇒ ¬ X₁₂₁∧ ¬ X₁₃₁ ∧ ¬ X₁₄₁∧ ¬ X₁₅₁ ∧ ¬ X₁₆₁∧ ¬ X₁₇₁ ∧ ¬ X₁₈₁∧ ¬ X₁₉₁

que l’on écrit de manière synthétiqueX₁₁₁ ⇒ ∧_l≠1 ¬ X_1l1 Au final il faudra écrire 9³ formules pour toutes les valeurs de i,j,k∈ [1,9] de la forme : X_ijk ⇒ ∧_l≠j ¬ X_ilk. Comme dans le cas de la propriété au plus un chiffre par case, une formulation alternative est de considérer toutes les formules ¬ X_ijk ∨ ¬ X_ilk avec l≠j
Même chose pour les colonnes et les carrés.
Lorsque la case (i,j) est pré-remplie avec le chiffre k, on introduira la contrainte : X_ijk.

On obtient ainsi un ensemble d’axiomes (on pourra estimer l’ordre de grandeur). Chaque modèle de cette théorie représente une solution du Sudoku. Il peut n’y en avoir aucune ou au contraire plusieurs. Le nombre de variables est 9³, ce qui fait que le nombre d’interprétations est 2^9³=2⁷²⁹≃ 10²¹⁹. Un traitement manuel de la table de vérité n’est pas envisageable mais il n’est pas très compliqué d’écrire un programme qui résout un tel problème automatiquement en utilisant la logique.

Les SAT-solvers utilisent des algorithmes sophistiqués pour pouvoir traiter des formules avec un très grand nombre de variables propositionnelles. Ils sont utilisés pour vérifier des programmes, ou bien pour résoudre des problèmes de planification qui seront modélisés de manière logique.

Sur le problème du Sudoku, on voit qu’utiliser des formules propositionnelles nécessite l’introduction de beaucoup de variables propositionnelles et d’axiomes. Au contraire en logique du premier ordre, il est possible de considérer les positions et les chiffres comme des objets de la logique et d’utiliser donc des variables d’objets pour les représenter. Au lieu des 729 variables propositionnelles, on introduit un seul symbole de prédicat à trois arguments pos(i,j,k) qui sera vrai lorsque le chiffre k est à la position (i,j). On a également besoin du symbole binaire d’égalité sur les objets.

Cela permet de factoriser la description avec un nombre plus réduit d’axiomes.

Exercice 13

A l’aide du symbole de prédicat pos(i,j,k) défini ci-dessus et de la relation d’égalité, donner des axiomes en logique du premier ordre qui décrivent les règles du Sudoku.
Le langage proposé est-il suffisant pour décrire la contrainte que le même chiffre n’apparaît pas dans le même “cadran” de la grille. Que proposez-vous pour résoudre ce problème ?
On veut contraindre les objets de cette théorie à être dans un ensemble avec exactement 9 valeurs. Comment peut-on traduire cette contrainte en formule logique ?

Compétences 4

Connaître la définition d’une théorie.
Savoir distinguer modélisation en calcul propositionnel et modélisation en logique du premier ordre.
Connaître la théorie de l’égalité.

1.5 Définition récursive sur les formules

On a vu que les formules pouvaient se représenter comme des arbres. On introduit dans cette section une méthode générale de définition récursive sur la structure des formules qui nous permet de définir des opérations ou propriétés mathématiques sur les formules ou bien de les manipuler par ordinateur.

Les formules atomiques pouvant faire référence à des termes, nous donnons également les éléments pour définir des fonctions de manière récursive sur les termes et raisonner par récurrence structurelle.

1.5.1 Définir une fonction

On peut définir une fonction G de l’ensemble des formules logiques dans un ensemble D quelconque en se donnant un ensemble d’équations que doit satisfaire cette fonction. Les équations sont de la forme G(t)=u avec u un élément de l’ensemble D. Il faut une équation pour chacune des constructions possibles de formule: formules atomiques (en particulier ⊤, ⊥), formules composées d’un connecteur propositionnel ¬ A, A∧ B, A∨ B, A⇒ B ou d’un quantificateur ∀ x, A, ∃ x, A.

Dans le cas des connecteurs propositionnels et des quantificateurs, le membre droit u peut utiliser la valeur de G sur des sous-formules de t (comme G(A) et G(B)). On parle de définition récursive.

On peut par exemple définir une fonction nbsymbp qui compte le nombre de connecteurs propositionnels dans une formule :

Dans les définitions ci-dessus p, A ou B ne sont pas des symboles logiques mais des variables mathématiques qui nous servent à définir la fonction (comme la variable x dans une définition f(x)=x+1), elles représentent n’importe quelle formule complexe.

Ce qui est important dans cette définition est qu’elle est complète car elle couvre tous les cas de formules, que pour chaque formule il n’y a qu’une seule équation qui s’applique et donc que la définition est non-ambigüe et finalement on dit qu’elle est bien fondée car les références à la fonction G dans les membres droits des équations se font sur des formules strictement plus petites que le membre gauche.

Ces équations définissent également un moyen de calcul de la valeur de G pour une formule donnée. Par exemple dans le cas de la formule A =^def (∀ x, P ⇒ Q) ⇒ ¬ Q ⇒ ¬ ∃ x, P on aura nbsymbp(A)=5.

Exercice 14 Modifier la définition précédente pour définir une fonction nbsymb qui compte le nombre de symboles logiques dans la formule, à savoir les connecteurs propositionnels comme dans nbsymbp mais aussi les quantificateurs ∀ et ∃.

Exercice 15 Donner les équations qui définissent la profondeur prof(A) d’une formule A, c’est-à-dire qui donne le nombre maximal de connecteurs et quantificateurs imbriqués. Dans le cas de la formule A précédente on aura prof(A)=4.

Restriction au calcul propositionnel

Le calcul propositionnel est le sous-ensemble du calcul des prédicats qui ne contient que des symboles de prédicat d’arité 0, qui sont appelés des variables propositionnelles et pas de quantificateur ni de termes. On peut de la même manière faire une définition récursive sur la structure d’une formule propositionnelle en décomposant le cas des formules atomiques en trois cas ⊥, ⊤ et les variables propositionnelles et en éliminant les deux cas des quantificateurs.

Calcul de la valeur de vérité d’une formule propositionnelle

Une fois que l’on se donne une interprétation I qui à chaque variable propositionnelle associe sa valeur de vérité, on peut définir une fonction val(I,P)∈B qui calcule la valeur de vérité d’une formule propositionnelle quelconque P par les équations suivantes

1.5.2 Raisonner sur les formules

Pour établir un résultat pour toutes les formules, on peut utiliser un raisonnement par récurrence sur la structure de la formule. Soit une propriété φ(P) qui dépend d’une formule P.

Ce principe de preuve est très utile lorsque l’on veut montrer des propriétés qui parlent de fonctions sur les formules qui sont elles-mêmes définies récursivement.

Exemple 11 On peut définir de manière récursive le nombre d’occurrences de sous-formules atomiques dans une formule logique :

nbatom(p)	=1 si p atomique
nbatom(¬ A)	=nbatom(A)
nbatom(∀ x, A)	=nbatom(A)
nbatom(∃ x, A)	=nbatom(A)

nbatom(A∧ B)	=nbatom(A)+nbatom(B)
nbatom(A∨ B)	=nbatom(A)+nbatom(B)
nbatom(A⇒ B)	=nbatom(A)+nbatom(B)

On peut ensuite montrer que pour toute formule P, on a nbatom(P)≤ 1+nbsymbp(P).

Pour faire cette preuve, on commence par expliciter la propriété φ(P) que l’on cherche à montrer par récurrence structurelle sur P. Dans notre cas, il s’agit de nbatom(P)≤ 1+nbsymbp(P). On doit examiner chacun des cas possibles pour la formule P:

Cas où P est une formule atomique p. Par définition de nbatom et nbsymbp, on a nbatom(p)=1 et nbsymbp(p)=0 donc on vérifie aisément que nbatom(p)≤ 1+nbsymbp(p) et donc φ(p) est vérifié.
Cas où P est une négation de la forme ¬ A avec A une formule quelconque. On suppose (hypothèse de récurrence) que φ(A) est vérifié et donc que nbatom(A)≤ 1+nbsymbp(A). Il faut montrer que φ(¬ A) est également vérifié. Par définition de nbatom et nbsymbp, on a nbatom(¬ A)=nbatom(A) et nbsymbp(¬ A)=1+nbsymbp(A). En utilisant l’hypothèse de récurrence on a donc
nbatom(¬ A)=nbatom(A)≤ 1+nbsymbp(A)=nbsymbp(¬ A)≤ 1+nbsymbp(¬ A)

et donc on a bien montré que φ(¬ A) était vérifiée.
Cas où P est une conjonction, disjonction ou implication de deux formules quelconques A et B, on note P=A∘ B avec ∘ l’un des trois connecteurs. En effet, dans cet exemple, ils jouent tous les trois le même rôle, il n’est donc pas nécessaire de distinguer les trois cas.
On suppose (hypothèses de récurrence) que φ(A) et φ(B) sont vérifiés et donc que nbatom(A)≤ 1+nbsymbp(A) et nbatom(B)≤ 1+nbsymbp(B).
Il faut montrer que φ(A∘ B) est également vérifié. Par définition de nbatom et nbsymbp, on a nbatom(A∘ B)=nbatom(A)+nbatom(B) et nbsymbp(A∘ B)=1+nbsymbp(A)+nbsymbp(B).
En utilisant les hypothèses de récurrence on a donc
nbatom(A∘ B) =nbatom(A)+nbatom(B)

≤ 1+nbsymbp(A) + 1+nbsymbp(B)

= 1+nbsymbp(A∘ B)

et donc on a bien montré que φ(A∘ B) était vérifiée.
Cas où P est une formule quantifiée de la forme ∀ x, A ou ∃ x, A avec A quelconque.
On suppose (hypothèse de récurrence) que φ(A) est vérifié et donc que nbatom(A)≤ 1+nbsymbp(A).
Il faut montrer que φ(∀ x, A) et φ(∃ x, A) sont également vérifiés. On traite seulement le cas ∀ x, A car celui de ∃ x, A est identique.
Par définition de nbatom et nbsymbp, on a nbatom(∀ x, A)=nbatom(A) et nbsymbp(∀ x, A)=nbsymbp(A). En utilisant l’hypothèse de récurrence on a donc
nbatom(∀ x, A)=nbatom(A)≤ 1+nbsymbp(A)=1+nbsymbp(∀ x, A)

et donc on a bien montré que φ(∀ x, A) était vérifiée.
La même preuve nous donne que φ(∃ x, A) est vérifié.

On a bien examiné tous les cas possibles et prouvé par récurrence sur la structure de la formule P, que pour toute formule logique P, on a nbatom(P)≤ 1+nbsymbp(P).

1.5.3 Définition récursive sur les termes

En logique du premier ordre, les formules font référence à des objets qui sont représentés syntaxiquement par des termes qui apparaissent en argument des symboles de prédicat au niveau des formules atomiques.

Soit F une signature, c’est-à-dire un ensemble de symboles de fonctions définis avec leur arité et X un ensemble de variables. On note F_n l’ensemble des symboles de F d’arité n et on rappelle que T(F,X) représente l’ensemble des termes bien formés construits à partir de cette signature et de ces variables.

De la même manière que l’on fait une définition récursive sur les formules, on peut construire une fonction G de manière récursive sur les termes, en se donnant un ensemble d’équations. Il y aura une équation dans le cas où le terme est une variable x et une équation pour chaque symbole d’objet. Si on a un symbole f d’arité n alors il y aura une équation G(f(t₁,…,t_n))=u avec la possibilité pour u de faire référence aux résultats de la fonction G sur les sous termes et donc de mentionner non seulement les termes t₁,…,t_n mais aussi les valeurs G(t₁),…,G(t_n).

Exemple 12 On se donne un langage avec une constante c, une fonction unaire f et une fonction binaire g.

On définit une fonction clos qui étant donné un terme t teste s’il est clos, c’est-à-dire s’il ne contient aucune variable, en utilisant les équations suivantes :

clos(x)	=faux si x est une variable
clos(c)	=vrai

clos(f(t))	=clos(t)
clos(g(t,u))	=clos(t) et clos(u)

Définition 1 (Définition récursive sur les termes) Soit F une signature, X un ensemble de variables et D un ensemble quelconque.

On suppose que l’on veut définir une application G qui prend en argument un terme et renvoie un élément de D, on a donc G∈T(F,X) → D. Pour cela on va se donner les objets suivants :

Une application V dans X → D;
Pour chaque constante c∈F₀, un élément g_c∈ D
Pour chaque symbole de fonction f∈F_n, une application G_f dans

T(F,X)×… × T(F,X)

◥
▼
◤

n fois

×

D×… × D

◥
▼
◤

n fois

→ D

.

Il existe une unique application G dans T(F,X) → D qui vérifie :

G(x)	=V(x)	(x∈X)
G(c)	=g_c	(c∈F₀)
G(f(t₁,…,t_n))	=G_f(t₁,…,t_n,G(t₁),…,G(t_n))	(f∈F_n)

Le fait que l’on puisse définir une telle application est une conséquence du fait que l’égalité sur les termes correspond à un critère syntaxique. Deux termes sont égaux s’ils ont la même représentation sous forme d’arbre, c’est-à-dire que deux termes qui débutent par des symboles différents sont différents.

En effet ce schéma permet de définir une application G telle que G(c)=1 pour les constantes et G(t)=2 pour tous les termes qui commencent par un symbole de fonction. Si on avait plus(0,0)=0 alors on en déduirait G(plus(0,0))=G(0) et donc 2=1.

Exemple 13 (Taille d’un terme) Le schéma de définition récursive précédent permet de définir l’application size qui compte le nombre de symboles dans un terme.

si x ∈ X alors size(x)=0
si c ∈ F₀ alors size(c)=1
si f ∈ F_n alors size(f(t₁,…,t_n))=1+size(t₁)+⋯+size(t_n)

Dans le cas d’une signature sur les entiers qui contient la constante 0, le symbole unaire S et le symbole binaire plus, soit t le terme plus(0,S(0)), il vérifie size(t)=4.

Exemple 14 (Hauteur d’un terme) Un autre exemple de définition récursive est l’application ht qui compte le nombre maximal de symboles imbriqués dans un terme.

si x ∈ X alors ht(x)=0
si c ∈ F₀ alors ht(c)=1
si f ∈ F_n alors ht(f(t₁,…,t_n))=1+ max(ht(t₁),…,ht(t_n))

Pour le terme t précédent on a ht(t)=3.

Exercice 16 Ecrire une fonction vars qui prend en argument un terme et renvoie l’ensemble des variables qui apparaissent dans ce terme.

Substitution

Nous avons déjà utilisé sans la définir formellement la notion de remplacement d’une variable par un terme. Ici on généralise cette opération par le remplacement en parallèle de plusieurs variables par des termes. Pour cela, on se donne une application σ∈X→T(F,X), appelée substitution qui associe un terme à chaque variable. On notera {x₁←u₁;…;x_n←u_n} la substitution σ telle que σ(x)=u_i si x=x_i et σ(x)=x sinon.

On définit pour chaque terme t, le résultat de la substitution dans t de toute variable x par σ(x) que l’on note t[σ].

Définition 2 (Substitution sur les termes, t[σ]) Si σ est de la forme {x₁←u₁;…;x_n←u_n}, alors le terme t[σ] sera noté t[x₁←u₁;…;x_n←u_n].

La définition de t[σ] se fait de manière récursive sur t:

si x ∈ X alors x[σ]=σ(x)
si c ∈ F₀ alors c[σ]=c
si f ∈ F_n alors f(t₁,…,t_n)[σ]=f(t₁[σ],…,t_n[σ])

Exemple 15 t=plus(mult(x,y),S(x)) et σ={x← mult(y,0);y←0}.
On a t[σ]=plus(mult( mult(y,0),0),S( mult(y,0)))

On peut montrer que le résultat de t[σ] ne dépend que de la valeur de la substitution σ sur les variables de t. De manière plus précise cela revient à montrer que si on a deux substitutions σ₁ et σ₂ ainsi qu’un terme t, si pour toute variable x∈vars(t) on a σ₁(x)=σ₂(x) alors t[σ₁]=t[σ₂]. La preuve se fait aisément par récurrence structurelle sur le terme t suivant le schéma ci-dessous.

Récurrence sur les termes

On a également un schéma de preuve par récurrence sur les termes de T(F,X) qui s’exprime de la manière suivante. Soit φ(t) une propriété mathématique qui dépend d’un terme t ∈ T(F,X). On suppose :

Exemple 16 On peut par exemple montrer la propriété suivante pour tout terme t ∈ T(F,X), ht(t) ≤ size(t).

Preuve: La preuve se fait par récurrence sur la structure du terme t. La propriété φ(t) à montrer est définie comme ht(t) ≤ size(t).

variable

si t est une variable x ∈ X, alors il faut montrer ht(x) ≤ size(x) qui est vrai car ht(x)=0 et size(x)=0

constante

si t est une constante c alors il faut montrer ht(c) ≤ size(c) qui est vrai car ht(c)=1=size(c).

symbole

si t est de la forme f(t₁,…,t_n) avec f ∈ F_n et t₁,…,t_n∈ T(F) des termes quelconques qui vérifient l’hypothèse de récurrence ht(t_i) ≤ size(t_i). On doit montrer ht(f(t₁,…,t_n)) ≤ size(f(t₁,…,t_n)).

ht(f(t₁,…,t_n))	= 1+max(ht(t₁),…,ht(t_n))	(déf de ht)
	≤ 1+ ht(t₁)+⋯ + ht(t_n)	(car ht(t_i)≥ 0)
	≤ 1+ size(t₁)+⋯ + size(t_n)	(hyp. de récurrence)
	=size(f(t₁,…,t_n))	(déf de size)

On en déduit que ht(t) ≤ size(t) est vérifié pour tout les termes du langage. □

Exercice 17 Sur la signature des arbres binaires qui comporte une constante є pour représenter une feuille et un symbole N binaire pour représenter un nœud interne. Définir une fonction feuilles qui compte le nombre de feuilles et une fonction noeuds qui compte le nombre de nœuds internes. Montrer que pour tout arbre t qui ne contient pas de variable, on a feuilles(t)=noeuds(t)+1.

Substitution sur les formules

On a défini formellement la fonction de substitution d’une variable par un terme dans un autre terme. On peut faire de même avec la définition de la substitution d’une variable par un terme dans une formule quelconque. On construit la fonction à l’aide d’équations récursives sur le structure de la formule.

La définition de la substitution d’une variable x par un terme t dans une formule P doit prendre en compte le problème de la capture possible d’une des variables du terme t par un des quantificateurs interne de P.

Définition 3 (Substitution P[x← t] d’une variable par un terme dans une formule) Soit x une variable et t un terme.

Formules atomiques :
- ⊥[x← t] =⊥
- ⊤[x← t] =⊤
- R(t₁,…,t_n)[x← t] = R(t₁[x← t],…,t_n[x← t])
Soit A une formule, (¬ A)[x← t]=¬(A[x← t])
Soient A et B des formules, si ∘ ∈ {∧,∨,⇒} alors (A∘ B)[x← t]=(A[x← t])∘ (B[x← t])
Soit P une formule et y une variable:
- si y=x alors (∀ y,Q)= ∀ x,Q et comme x n’est pas libre dans ∀ x,Q on a (∀ y,Q)[x← t] = (∀ x,Q)[x← t] = ∀ x,Q
- de même si y=x alors (∃ y,Q)[x← t] = (∃ x,Q)[x← t] = ∃ x,Q
- si y≠x et y∉vars(t) alors (∀ y,Q)[x← t] = ∀ y,(Q[x← t]) (la substitution se propage sous le quantificateur, sans risque de capture puisque la variable liée y n’apparaît pas dans t)
- si y≠x et y∉vars(t) alors (∃ y,Q)[x← t] = ∃ y,(Q[x← t])

Cette définition est donc partielle dans le cas des formules avec quantificateurs si une variable liée dans la formule apparaît aussi dans le terme que l’on veut substituer. Cependant en procédant à un renommage des variables liées dans les quantificateurs, on peut toujours se ramener à une situation dans laquelle la substitution sera possible.

Exercice 18 La définition 2 nous donne les axiomes de la théorie de l’égalité pour un langage quelconque. Soient t et u deux termes du langage et P une formule quelconque. On rappelle que P[x← t] représente la formule P dans laquelle on remplace la variable libre x par le terme t.

Montrer par récurrence sur la structure de la formule, que la règle de substitution dans un contexte arbitraire est valide :

t=u ⇒ P[x← t] ⇒ P[x← u]

On pourra faire la preuve dans le cas particulier d’une signature qui ne contient qu’une constante a, un symbole de fonction binaire g et un symbole de prédicat binaire Q.
On donnera l’ensemble des axiomes de la théorie de l’égalité associée à ces symboles.
On commencera par montrer par récurrence sur la structure du terme v que la formule suivante est valide :
t=u ⇒ v[x← t]=v[x← u]

Cette affirmation peut sembler paradoxale, c’est pourtant une propriété toujours vraie. En effet soit tout le monde a les yeux bleus et l’affirmation est vraie, soit il existe une personne qui n’a pas les yeux bleus, que l’on nomme a. La propriété yeux-bleus(a)⇒ ∀ y, yeux-bleus(y) est vraie car de la forme A⇒ B avec A est faux. On en déduit le résultat.

Noter la différence de parenthésage avec la phrase précédente. Cette nouvelle affirmation, contrairement à la précédente n’est pas toujours vérifiée.

Chapitre 1 Maîtriser le langage logique