Eléments de logique pour l’informatique 2022–23
Annexe A Correction des exercices du cours
A.1 Exercices du chapitre 1
Exercice 1
-
∀ x, (joue(self,x)⇒ ami(self,x))
- ∀ x, ∃ y, ami(x,y)
- ¬ (∃ x, (joue(self,x) ∧ ami(self,x))) ou de manière équivalente
∀ x, ((¬ joue(self,x)) ∨ (¬ ami(self,x))
- ∃ x y, (joue(self,x) ∧ joue(self,y)∧ ¬(x=y)) sans la mention de x≠y la formule est vraie dès qu’il existe une personne avec qui je joue.
Exercice 2
∀ x y, ((pair(x)∧ pair(y))⇒ pair(x+y))
Exercice 3
-
∀ x∈ℕ,P correspond à ∀ x,(N(x)⇒ P)
- ∃ x∈ℕ,P correspond à ∃ x,(N(x)∧ P)
Exercice 4
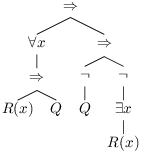
La formule parenthésée est (∀ x, (R(x) ⇒ Q)) ⇒ ((¬ Q) ⇒ (¬ (∃ x, R(x)))) et sous forme d’arbre :
Exercice 5
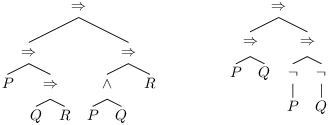
Les formules parenthésées sont (P ⇒ (Q ⇒ R)) ⇒ ((P ∧ Q) ⇒ R) et
(P ⇒ Q) ⇒ ((¬ Q) ⇒ (¬ P))
et sous forme d’arbre
Exercice 6
-
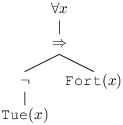
∀ x, ¬ Tue(x) ⇒ Fort(x) correspond au minimum de parenthèses
- ∀ x, ((¬ Tue(x)) ⇒ Fort(x)) correspond à la formule complètement parenthésée
- La forme arborescente est
Exercice 7
La seule variable libre de la formule : ∀ b, b > 0 ⇒
∃ q, ∃ r, a = b × q + r ∧ r < b est la variable a.
Exercice 8
-
La formule ((P ⇒ Q) ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors P ⇒ Q est vrai et donc (P ⇒ Q) ⇒ P est faux et donc ((P ⇒ Q) ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
- La formule (¬ P ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors ¬ P est vrai et donc ¬ P ⇒ P est faux et donc (¬ P ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
Exercice 9
-
L’inscription sur la porte 1 correspond à la formule A1 =def P1 ∧ ¬ P2,
- L’inscription sur la porte 2 correspond à la formule A2≡ (P1 ∧ ¬ P2)∨ (P2 ∧ ¬ P1),
- Une seule de ces inscriptions est vraie donc la formule (A1∧ ¬ A2) ∨ (A2∧ ¬ A1) est vraie.
On peut faire une table de vérité de cette dernière formule en fonction des valeurs de P1 et P2 et chercher dans quels cas elle est vraie.
On peut aussi raisonner directement.
Comme A2 est de la forme A1 ∨ B, si A1 est vrai alors A2 est vrai et donc la troisième formule est fausse.
Donc A1 est faux et A2 est vrai et on a P2 ∧ ¬ P1 donc il faut ouvrir la deuxième porte.
Exercice 10
La formule (∀ x, P(x)) ⇒ ∃ x, P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ∀ x, P(x). L’interprétation de P est vraie pour toutes les valeurs dans le domaine D. Comme le domaine est non vide, on peut choisir d∈ D. L’interprétation de P est vraie pour d et donc ∃ x, P(x) est vraie dans cette interprétation.
La formule ¬(∀ x, P(x)) ⇒ ∃ x, ¬ P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ¬(∀ x, P(x)). Cette interprétation rend faux ∀ x, P(x) ce qui veut dire qu’il existe d∈ D pour lequel l’interprétation P est fausse et donc l’interprétation de ∃ x, ¬ P(x) est vraie.
Exercice 11
t ≤ u =def ∃ n,
n+t=u.
-
∀ x, 0 ≤ x se réécrit en ∀ x, ∃ n, n+0=x. Soit x quelconque, on choisit pour n la valeur x. Il faut alors montrer x+0=x qui est l’axiome 4 de la théorie arithmétique.
- ∀ x y, x ≤ y ⇔ S(x) ≤ S(y) se réécrit en
∀ x y, (∃ n, n+x=y) ⇔ (∃ n, n+S(x)=S(y)). Soit x et y quelconques, on montre les deux côtés de l’équivalence.
Si ∃ n, n+x=y, soit n tel que n+x=y, on a S(n+x)=S(y) (propriété de la théorie de l’égalité). On en déduit n+S(x)=S(y) (axiome 5 de l’arithmétique) et donc ∃ n, n+S(x)=S(y).
Réciproquement si ∃ n, n+S(x)=S(y), soit n tel que n+S(x)=S(y), on en déduit S(n+x)=S(y) (axiome 5 de l’arithmétique). On en déduit n+x=y (axiome 3 de l’arithmétique) et donc ∃ n, n+x=y.
- transitivité : ∀ x y z, x ≤ y ⇒ y ≤ z ⇒
x ≤ z se réécrit en (∃ n, n+x=y)⇒ (∃ m, m+y=z) ⇒ (∃ p, p+x=z).
Soit x,y et z quelconques, on suppose ∃ n, n+x=y et ∃ m, m+y=z vrai et donc soit n et m tels que n+x=y et m+y=z. Par la théorie de l’égalité, on a m+(n+x)=m+y et par la transitivité de l’égalité on en déduit m+(n+x)=z. L’associativité de l’addition (non démontrée) permet d’en déduire que (m+n)+x=z
et donc ∃ p, p+x=z ce qui conclut la preuve.
Exercice 12
Les définitions utilisent la notion d’ordre strict t<u qui peut se définir par ∃ n,
S(n+t)=u.
-
Le fait que r est le résultat de la division entière
de x par y peut se représenter par la formule
∃ r, x = d× y +r ∧ r < y.
- Le fait que
r est le reste modulo de la division entière de x
par y peut se représenter par la formule ∃
d, x = d× y + r ∧ r < y.
- Si on remplace y par 0 dans la définition de divisibilité, on obtient la formule
∃ r, x = d× 0 +r ∧ r < 0 qui se développe en ∃ r, x = d× 0 +r ∧ (∃ n, S(n+r) = 0) formule qui est toujours fausse si on se place dans un monde qui satisfait les axiomes de la théorie arithmétique et en particulier ∀ x, S(x)≠0.
- Pour représenter le résultat de la division de a par b à l’aide d’un prédicat à trois arguments, il suffit d’introduire une nouvelle variable d et d’utiliser la formule div(a,b,d).
Dans le cas de (x/y)/z=x/(y× z), ill y a trois opérations de division, on introduit donc trois nouvelles variables d1, d2 et d3. d1 est le résultat de la division de x par y, ce qui se traduit par
div(x,y,d1), d2 est le résultat de la division de x/y (c’est-à-dire d1) par z ce qui se traduit par
div(d1,z,d2), finalement d3 est le résultat de la division de x par y× z ce qui se traduit par
div(x,y× z,d3).
Il suffit alors d’exprimer que sous ses hypothèses on a d2=d3. Ce qui s’écrit
| ∀ d1 d2 d3, div(x,y,d1)∧ div(d1,z,d2)∧ div(x,y× z,d3)⇒ d2=d3 |
Il est possible de montrer que la relation div est fonctionnelle c’est-à-dire que div(x,y,d1)∧ div(x,y,d2)⇒ d1=d2, la formule précédente peut donc se simplifier en | ∀ d1 d2, div(x,y,d1)∧ div(d1,z,d2)⇒ div(x,y× z,d2) |
Exercice 13
Il est nécessaire en plus du prédicat pos(i,j,k) qui exprime que le chiffre k est sur la case (i,j) de disposer du prédicat d’égalité pour pouvoir dire qu’un chiffre apparait au plus une fois.
-
Au plus un seul chiffre k par case (i,j): ∀ i j k, pos(i,j,k) ⇒ ∀ l, ¬ l=k⇒ ¬ pos(i,j,l)
- Chaque chiffre k apparaît sur chaque ligne i au moins dans une colonne j:
∀ i k, ∃ j, pos(i,j,k)
- Chaque chiffre k apparaît au plus une fois sur chaque ligne i (s’il est dans la colonne j, il n’est pas dans une autre colonne) :
∀ i j1 j2 k, pos(i,j1,k)∧ pos(i,j2,k)⇒ j1=j2
- Le cas des colonnes est analogue à celui des lignes. On traite ici la notion de carré. Si on veut éviter de traiter chaque valeur de ligne et de colonne individuellement, on peut introduire un symbole de fonction tiers unaire qui, étant donné une ligne ou une colonne, va nous dire dans quel tiers du tableau elle se trouve (premier, deuxième ou troisième). On peut ainsi tester si deux positions (i1,j1) et(i2,j2) seront dans le même carré si et seulement si les indices de ligne sont dans le même tiers du tableau et de même pour les indices de colonnes.
Pour représenter le fait que chaque chiffre k apparaît au plus une fois dans chaque carré on utilisera la formule :
| ∀ i1 i2 j1 j2 k, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2) |
| ⇒ pos(i1,j1,k)∧ pos(i2,j2,k) |
| ⇒ i1=i2∧ j1=j2 |
|
On peut aussi représenter le fait que chaque chiffre apparaitra au moins une fois dans chaque carré de la manière suivante :
| ∀ i1 j1 k, ∃ i2 j2, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2)∧ pos(i2,j2,k) |
Les deux formules sont redondantes dès lors qu’il y a 9 valeurs et 9 cases. En effet, on a écrit qu’il y avait au moins une valeur par case et qu’il ne pouvait pas y avoir deux fois la même valeur, donc chaque valeur va apparaître au moins une fois car une application injective (resp. surjective) d’un ensemble fini dans un ensemble de même cardinal est bijective.
- On exprime dans la logique le fait qu’on a 9 valeurs possibles pour les lignes, les colonnes et les chiffres dans les cases. Cela se fait en ajoutant 9 constantes :1,…,9. Il faut un axiome qui dit que l’univers est formé uniquement de ces 9 éléments
∀ x,x=1∨ …∨ x=9 auquel il faut ajouter les 36 axiomes qui disent que les constantes sont différentes deux à deux ¬1=2,¬1=3,…,¬1=9,¬2=3,…, ¬8=9.
Il faudra aussi ajouter les 9 axiomes qui permettent de raisonner sur la fonction tiers à savoir
tiers(1)=1,tiers(2)=1,tiers(3)=1,…,,tiers(9)=3.
Exercice 14
| nbsymb(p) | =0 si p atomique |
| nbsymb(¬ A) | =1+ nbsymb(A) |
| nbsymb(∀ x, A) | = 1+nbsymb(A) |
| nbsymb(∃ x, A) | = 1+nbsymb(A) |
| |
|
| | nbsymb(A∧ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A∨ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A⇒ B) | =1+ nbsymb(A)+nbsymb(B) |
|
Exercice 15
| prof(p) | =0 si p atomique |
| prof(¬ A) | =1+ prof(A) |
| prof(∀ x, A) | = 1+prof(A) |
| prof(∃ x, A) | = 1+prof(A) |
| |
|
| | prof(A∧ B) | =1+ max(prof(A),prof(B)) |
| prof(A∨ B) | =1+ max(prof(A),prof(B)) |
| prof(A⇒ B) | =1+ max(prof(A),prof(B)) |
|
Exercice 16
-
si x ∈ X alors vars(x)={x}
- si c ∈ F0 alors vars(c)=∅
- si f ∈ Fn alors vars(f(t1,…,tn))=
vars(t1)∪…∪ vars(tn)
Exercice 17
On considère ici des termes qui ne contiennent pas de variable
-
définition de feuilles
| feuilles(є)=1 feuilles(N(l,r)) = feuilles(l)+feuilles(r) |
- définition de noeuds
| noeuds(є)=0 noeuds(N(l,r)) = 1+noeuds(l)+noeuds(r) |
- preuve par récurrence que pour tout terme t sans variable, on a feuilles(t)=noeuds(t)+1.
-
cas où t est la constante є on a
feuilles(є)=1 et noeuds(є)=0 d’où le résultat.
- cas où t est de la forme N(l,r) avec l et r deux sous-arbres qui vérifient l’hypothèse de récurrence
feuilles(l)=noeuds(l)+1 et feuilles(r)=noeuds(r)+1.
On a
| feuilles(N(l,r)) | = feuilles(l)+feuilles(r) | définition de feuilles |
| | =noeuds(l)+1+noeuds(r)+1 | hypothèses de récurrence |
| | =noeuds(N(l,r))+1 | définition de noeuds |
|
On en déduit que la propriété est vraie pour tous les arbres.
Exercice 18
La théorie de l’égalité contient les axiomes pour la reflexivité, la symétrie et la transitivité ainsi que des axiomes pour les symboles de fonctions et les prédicats d’arité au moins 1.
Dans le cas de la signature qui est donnée, il y aura donc deux axiomes
-
∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ g(x1,y1)=g(x2,y2)
- ∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ Q(x1,y1)⇒ Q(x2,y2)
On veut montrer que la formule t=u ⇒ P[x← t]⇒ P[x← u] est valide pour n’importe quelle formule P du langage.
On commence par montrer un cas particulier à savoir que
la formule t=u ⇒ v[x← t]=v[x← u] est valide pour n’importe quel terme v du langage.
On se place dans une interprétation qui rend vraie la formule t=u (et les axiomes de l’égalité) et on utilise une récurrence sur la structure du terme v pour montrer que
v[x← t]=v[x← u] est également vraie dans cette interprétation.
-
si v est une variable z alors soit z=x et la formule devient t=u qui est vraie par hypothèse sur l’interprétation, soit z≠x et la formule devient z=z qui est vraie par reflexivité de l’égalité.
- si v est la constante a alors la formule devient a=a qui est vraie par reflexivité de l’égalité.
- si v est de la forme g(v1,v2) avec v1 et v2 qui vérifient l’hypothèse de récurrence à savoir v1[x← t]=v1[x← u] et v2[x← t]=v2[x← u]. On a g(v1,v2)[x← t]=g(v1[x← t],v2[x← t]), par définition de la substitution. En appliquant les hypothèses de récurrence et l’axiome 1 de l’égalité ci-dessus, on obtient g(v1,v2)[x← t]=g(v1[x← u],v2[x← u]) et donc finalement
g(v1,v2)[x← t]= g(v1,v2)[x← u]
On montre ensuite par récurrence sur la formule P que pour tous les termes t et u et toute interprétation qui rend vraie t=u, on a P[x← t]⇒ P[x← u] est vraie quelque soit l’environnement pour les valeurs des variables libres de P[x← t].
-
Si P est une formule atomique :
Si P est ⊥ ou ⊤ qui ne contient pas x alors il faut montrer P⇒ P qui est une tautologie.
Si P est de la forme Q(v1,v2) alors il faut montrer
Q(v1,v2)[x← t]⇒ Q(v1,v2)[x← u]
Par definition de la substitution, cela revient à montrer
Q(v1[x← t],v2[x← t])⇒ Q(v1[x← u],v2[x← u])
en utilisant l’axiome 2 de la théorie de l’égalité, il suffit de montrer
v1[x← t]=v1[x← u]∧ v2[x← t]=v2[x← u]. Or cette propriété est vraie d’après ce que nous avons établi précédemment.
- Si P est de la forme ¬ A alors il faut montrer (¬ A)[x← t]⇒ (¬ A)[x← u], c’est-à-dire ¬ (A[x← t])⇒ ¬ (A[x← u]) en prenant la contraposée, on est ramené à montrer A[x← u]⇒ A[x← t]. Comme une interprétation qui rend vraie t=u rend aussi vraie u=t par symétrie de l’égalité, on peut appliquer l’hypothèse de récurrence à A avec les termes u et t.
- Si P est de la forme A∘ B avec ∘ l’un des 2 connecteurs propositionnels ∧ ou ∨, alors il faut (A∘ B)[x← t]⇒ (A∘ B)[x← u], c’est-à-dire (A[x← t]∘ B[x← t])⇒ (A[x← u]∘ B[x← u]) or par hypothèse de récurrence on A[x← t]⇒ A[x← u] et B[x← t]⇒ B[x← u]. On conclut en utilisant les propriétés des connecteurs (si A1⇒ A2 et B1⇒ B2 alors A1∧ B1⇒ A2∧ B2 et A1∨ B1⇒ A2∨ B2.
- Si P est de la forme A⇒ B, le raisonnement est presque le même sauf que
la propriéte (A1⇒ B1)⇒ (A2⇒ B2) est une conséquence de A2⇒ A1 et B1⇒ B2. Il faut donc intervertir t et u comme dans le cas de la négation.
- Si P est de la forme ∀ z,A. On choisit la variable liée z pour qu’elle ne soit pas libre ni dans t ni dans u (sinon la substitution n’est pas définie) et qu’elle soit différente de x (sinon (∀ x,A)[x← v]=(∀ x,A) et la propriété est trivialement vraie.
On doit montrer (∀ z,A)[x← t]⇒ (∀ z,A)[x← u], c’est-à-dire
(∀ z,(A[x← t]))⇒ ∀ z,(A[x← u])
Par hypothèse de récurrence on sait que (A[x← t])⇒ (A[x← u])
quelle que soit la valeur que l’on donne pour z dans l’environnement.
On en déduit que (∀ z,(A[x← t]))⇒ (A[x← u]) est vraie pour toute valeur possible de z. En effet si on prend une valeur pour z et que ∀ z,(A[x← t]) est vrai alors A[x← t] est a fortiori vrai pour cette valeur de z et donc A[x← u].
De (∀ z,(A[x← t]))⇒ (A[x← u]) vrai pour toutes les valeurs de z, on déduit que (∀ z,(A[x← t]))⇒ ∀ z,(A[x← u]) est vrai.
On procède de manière analogue pour le quantificateur existentiel.
Si (A[x← t])⇒ (A[x← u]) est vrai
pour toute valeur de z alors (∃ z,(A[x← t]))⇒ ∃ z,(A[x← u]) est vrai. En effet si ∃ z,(A[x← t]) est vrai alors il existe une valeur v0 telle que A[x← t] est vraie pour cette valeur de z, donc A[x← u] est vraie pour cette même valeur de z (hypothèse de récurrence) et donc ∃ z,A[x← u] est vraie.