Manipuler les formules de la logique

Dans ce chapitre, nous allons aborder la logique et les formules sur le plan syntaxique, c’est-à-dire que nous chercherons à établir des propriétés logiques des formules (validité, satisfiabilité) par des transformations sans passer par la notion de modèle. Nous étudierons tout d’abord des mises en formes canoniques de formules logiques et en particulier la mise en forme clausale. Nous introduirons également la représentation des formules propositionnelles comme des diagrammes de décision binaires. Finalement nous introduirons des systèmes de déduction pour les formules et en particulier le calcul des séquents.

3.1 Formes normales

Dans le chapitre 2 nous avons introduit la forme normale de négation d’une formule. Une formule en forme normale de négation ne contient pas de connecteur ⇒ (ou ⇔) et les seuls négations portent sur des symboles de prédicat. Grace aux lois de de Morgan, il est possible de propager les symboles de négation jusqu’aux symboles de prédicat et donc toute formule est équivalente à une formule en forme normale de négation. De plus cette transformation ne change pas la taille de la formule.

3.1.1 Forme normale de négation

Définition 1 (Littéral) On appelle littéral une formule qui est soit une formule atomique, soit de la forme ¬ R(t₁,…,t_n) avec R un symbole de prédicat.

Dans la suite, on parlera d’instance de prédicat pour parler d’une formule de la forme R(t₁,…,t_n) avec R un symbole de prédicat. Une formule atomique est soit une instance de prédicat soit de la forme ⊤ ou ⊥. Dans le cas propositionnel, les instances de prédicat sont juste les variables propositionnelles.

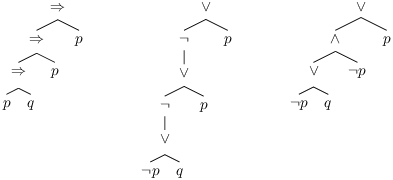
Proposition 1 Toute formule est équivalente à une formule en forme normale de négation, c’est-à-dire qui ne comporte pas de connecteur ¬ sauf dans un littéral et n’utilise que les connecteurs ⊤,⊥,∨ et ∧ et les quantificateurs ∀ et ∃.

Preuve: Pour définir un algorithme qui calcule la forme normale de négation d’une formule, on construit deux fonctions de manière récursive : fnn qui étant donnée une formule quelconque P, construit une formule en forme normale de négation équivalente à P et neg qui étant donnée une formule quelconque P, construit une formule en forme normale de négation équivalente à ¬ P.

On montre ensuite par récurrence structurelle sur la formule P que fnn(P) et neg(P) sont en forme normale de négation et que de plus fnn(P)≡ P et neg(P)≡ ¬ P □

Exemple 1 Soient p et q des variables propositionnelles et soit la formule ((p ⇒ q) ⇒ p) ⇒ p que l’on veut mettre en forme normale de négation. On élimine d’abord les implications, cette formule devient : ¬ (¬ (¬ p ∨ q) ∨ p) ∨ p On peut ensuite repousser les négations en commençant par l’extérieur. On obtient la formule : ((¬ p ∨ q) ∧ ¬ p)) ∨ p qui peut se simplifier en ¬ p ∨ p puis en ⊤. La représentation de la formule initiale, puis après élimination des implications et enfin sous forme normale de négation donne donne :

3.1.2 Clauses

Définition 2 (Clause) On appelle clause une formule qui n’utilise que des littéraux et la disjonction.

Un litteral tout seul est une clause dans laquelle il n’y a pas de disjonction. Si on veut faire apparaître une disjonction, on peut toujours rééecrire le littéral l en l∨ ⊥.

Exemple 2 Soi p,q des variables propositionnelles.

⊥, p,⊤,¬ p,p∨ q,p∨ q∨¬ p sont des clauses.
p∧ q,p∧ ⊤, p⇒ q ne sont pas des clauses.

Etre une clause est une propriété syntaxique des formules. Une formule peut être équivalente à une clause sans être une clause elle-même.

Les clauses peuvent se simplifier. La disjonction est associative et commutative, on a également P∨ P≡ P, P∨ ¬ P≡ ⊤, P∨ ⊤ ≡ ⊤, P∨ ⊥ ≡ P. Une clause peut donc soit être de la forme ⊥ ou ⊤, soit s’écrire l₁∨ l₂∨… ∨ l_n avec l_i un littéral autre que ⊥ ou ⊤. On peut représenter une clause comme un ensemble de litteraux tous distincts. La clause qui correspond à la formule atomique ⊥ est appelée clause vide elle correspond par convention à un ensemble vide de littéraux. Si une clause contient une instance de prédicat et sa négation alors elle est de la forme p∨¬ p∨ Q et se simplifie en ⊤.

On peut donc se ramener à une clause dans laquelle chaque instance de prédicat R(t₁,…,t_n) apparaît au plus une fois sous forme positive ou négative (¬ R(t₁,…,t_n)).

Proposition 2 Une clause est équivalente à ⊤ ou ⊥ ou bien à une une disjonction d’instances de prédicats (sous forme positive ou négative) dans laquelle chaque instance apparaît au plus une fois.

Preuve: Si une instance de prédicat p apparaît deux fois sous forme positive ou deux fois sous forme négative, alors en utilisant p∨ p≡ p on peut retirer une des occurrences sans changer la valeur de la formule. Si une instance de prédicat p apparaît une fois sous forme positive et une fois sous forme négative alors, en utilisant p∨ ¬ p ≡ ⊤, on peut remplacer ces deux occurrences par la formule ⊤. Une clause qui contient ⊤ est simplement équivalente à ⊤ (on dira que la clause est triviale). Si une clause est de la forme P∨⊥ on peut la simplifier en la clause P. □

Une clause est donc caractérisée par un ensemble d’instances de prédicats, chacun associé à un signe pour indiquer s’il apparait en position positive ou négative. On peut représenter une clause not triviale comme un ensemble d’instance de prédicats associés à des booléens (true si l’instance apparait positivement et false si elle apparait négativement).
Par exemple la clause p∨¬ q peut se représenter par l’ensemble {(p,true);(q,false)}.
Par convention, la clause associée à un ensemble vide de littéraux est interprétée comme la formule fausse ⊥. En effet une disjonction de formules est vraie lorsque l’une des formules qui forme la disjonction est vraie. S’il n’y a pas de formule, alors la propriété est fausse.

Exercice 1 Donner les équations récursives d’une fonction clauseset qui étant donnés un ensemble d’instances de prédicats, chacun associé à un booléen représentant sa polarité, construit la formule correspondante sous forme de clause.

Proposition 3 Soient L₁ et L₂ des ensembles de littéraux, si L₁⊆ L₂ alors la clause correspondant à L₂ est une conséquence logique de la clause correspondant à L₁.

Preuve: Si L₁ est un ensemble vide alors la clause correspondante est ⊥ et toute propriété est conséquence logique de ⊥. Sinon soit C₁ (resp. C₂, resp. C₃) la clause correspondant à L₁ (resp. L₂, resp. L₂ ∖ L₁). On a C₂ ≡ C₁ ∨ C₃ et donc comme C₁ ∨ C₃ est une conséquence logique de C₁, on en déduit que C₂ est une conséquence logique de C₁. □

3.1.3 Formes normales conjonctives et disjonctives

Définition 3 (Forme normale conjonctive, forme clausale) Une formule est dite en forme normale conjonctive si elle s’écrit comme une conjonction de clauses. On peut représenter une formule en forme normale conjonctive par un ensemble de clauses, on parle alors de forme clausale. Par convention, la conjonction d’un ensemble vide de formules est interprétée comme la formule vraie ⊤.

La conjonction de formules est vraie lorsque toutes les formules qui forment la conjonction sont vraies. S’il n’y a pas de formule, alors la propriété est vraie.

Proposition 4 Toute formule P propositionnelle admet une forme normale conjonctive, c’est-à-dire qu’il existe une formule Q équivalente à P et qui est en forme normale conjonctive.

Pour démontrer ce résultat, nous allons utiliser une autre propriété qui dit que toute fonction booléenne f à n arguments peut être associée a une formule Q en forme normale conjonctive telle que f=F(Q). En appliquant ce résultat à la fonction booléenne F(P) associée à P, on aura démontré le résultat de la proposition 4.

Proposition 5 Pour toute fonction booléenne f à n arguments, on peut trouver une formule Q en forme normale conjonctive telle que f=F(Q).

Preuve: On s’intéresse à l’ensemble Z des n-uplets pour lesquels la fonction f est fausse, c’est-à-dire

Dans la table de vérité, il suffit de s’intéresser aux lignes où la valeur de la formule est F. L’ensemble Z est fini. Si cet ensemble est vide alors f=F(⊤) qui est en forme normale conjonctive. On cherche une formule propositionnelle Q qui dépend des variables p₁,…,p_n correspondant à f. La variable propositionnelle p_i correspond à la propriété “le i-ème argument de f est vrai”. La propriété Q doit être vraie lorsque la fonction est vraie et donc doit exprimer que les arguments ne sont pas dans Z. Pour un élément (b₁,…,b_n), la formule qui dit que les arguments ne correspondent pas à cette valeur est l₁ ∨ l₂ ∨ … ∨ l_n avec l_i=p_i si b_i=F et l_i=¬ p_i si b_i=V. Cette formule est une clause. Il suffit ensuite de prendre la conjonction des clauses pour chaque élément de Z. □

Exemple 3 Soit la formule P =^def (p ⇒ q) ⇒ (¬ p ∧ q), on commence par écrire la table de vérité :

p	q	¬ p ∧ q	p ⇒ q	(p ⇒ q) ⇒ (¬ p ∧ q)
V	V	F	V	F
V	F	F	F	V
F	V	V	V	V
F	F	F	V	F

Les lignes qui nous intéressent sont la première et la dernière et on doit exprimer une formule qui dit exactement que l’on n’est pas dans un de ces deux cas.

La formule qui dit que l’on n’est pas dans le cas de la ligne 1 est ¬ p ∨ ¬ q et la formule qui dit que l’on n’est pas dans le cas de la ligne 4 est p ∨ q.

La forme normale conjonctive est donc (¬ p ∨ ¬ q) ∧ (p ∨ q).

Mise en forme normale conjonctive syntaxique

Construire la table de vérité d’une formule est trop complexe en général et donc on va plutôt utiliser des méthodes syntaxiques. La formule (a ∧ b) ∨ c n’est pas en forme normale conjonctive car il y a une disjonction qui porte sur une formule qui n’est pas un littéral. La règle de distributivité permet d’inverser les conjonctions et les disjonctions.

On en déduit un algorithme de mise en forme normale conjonctive. Pour cela, on construit une fonction fnc(P) qui calcule un ensemble de clauses équivalent à P et on utilise de manière auxiliaire une fonction fnc-neg(P) qui construit un ensemble de clauses équivalent à ¬ P. On aura besoin d’une autre fonction auxiliaire sh, qui prend en argument deux ensembles de clauses E et E′ et construit un nouvel ensemble de clauses avec toutes les combinaisons possibles C∨ C′ avec C∈ E et C′∈ E′, c’est-à-dire que sh(E,E′)={C∨ C′|C∈ E, C′∈ E′}. Si E contient n clauses et Si E′ contient p clauses alors sh(E,E′) peut contenir jusqu’à n× p clauses (il pourrait y en avoir moins si certaines clauses se simplifient).

Forme normale disjonctive

Définition 4 (Forme normale disjonctive)

Une conjonction élémentaire est une formule uniquement composée de littéraux et de conjonctions.
Une formule P est en forme normale disjonctive si elle s’écrit comme une disjonction de conjonctions élémentaires.

Proposition 6 Pour toute formule propositionnelle P, il existe une formule Q équivalente en forme normale disjonctive.

Preuve: Comme précédemment, on peut construire la table de vérité de la formule P par rapport aux variables propositionnelles {p₁,…,p_n}. On s’intéresse à l’ensemble O des n-uplets (b₁,…,b_n), pour lesquels la table de vérité donne la valeur vrai. Pour chaque ligne on construit une conjonction élémentaire l₁ ∧ l₂ ∧ … ∧ l_n avec l_i=p_i si b_i=V et l_i=¬ p_i si b_i=F. Il suffit ensuite de prendre la disjonction de ces formules pour trouver une formule équivalente à P. □

Exemple 4 En reprenant la formule P de l’exemple 3, on obtient la forme normale disjonctive :

(p∧ ¬ q) ∨ (¬ p ∧ q)

Si une formule est en forme normale disjonctive alors il est facile de trouver un modèle. On suppose que les branches de la disjonction sont en forme “simplifiée” c’est-à-dire qu’une variable propositionnelle apparaît dans un seul littéral. Il suffit de choisir une des branches de la disjonction. Pour chaque variable propositionnelle x qui apparaît dans un littéral l on prend dans le modèle x↦ V si l=x et x↦ F si l=¬ x. Il peut arriver qu’il n’y ait aucune composante en forme simplifiée: c’est le cas où la formule initiale est équivalente à ⊥ et donc il n’y a pas de modèle.

Cependant, la mise en forme normale n’est pas forcément la meilleure manière de trouver un modèle. En effet, cette forme normale peut être exponentiellement plus grosse que la formule initiale. C’est le cas par exemple de la formule (a₁∨ b₁) ∧…∧ (a_n ∨ b_n) qui a 2n variables et 2n−1 connecteurs. La forme normale disjonctive s’écrit ∨_{x_i∈{a_i,b_i}}(x₁∧… ∧ x_n). Il y a donc 2ⁿ disjonctions.

Mise en forme normale conjonctive efficace

Lorsqu’une formule propositionnelle est en forme normale conjonctive, il est facile de voir si elle est valide. En effet si l’ensemble des clauses n’est pas vide, on en choisit une qui est de la forme l₁∨… ∨ l_n que l’on rend fausse en choisissant une interprétation dans laquelle chacun des l_i est faux ce qui est possible car ils portent tous sur des variables propositionnelles différentes. Si une des clauses de la forme normale conjonctive est fausse alors il en est de même de la formule.

La forme normale conjonctive de la formule (a₁ ∧ b₁) ∨ … ∨ (a_n ∧ b_n) s’écrit ∧_{c_i∈{a_i,b_i}}c₁∨… ∨ c_n qui contient 2ⁿ clauses. Cette complexité est intrinsèque car liée à la complexité de décider si une formule propositionnelle est valide.

La forme normale conjonctive est équivalente à la formule initiale. Pour la démonstration automatique, cette équivalence n’est pas forcément nécessaire. Si on ne s’intéresse qu’à la satisfiabilité, on peut se permettre de transformer la formule P en une formule Q, telle que P et Q ne sont pas équivalentes, mais seulement equisatisfiable. C’est-à-dire que P est satisfiable si et seulement si Q. Cela nous permet d’introduire de nouvelles variables propositionnelles dans Q pour éviter l’explosion combinatoire.

Dire que P et Q sont équivalents c’est dire que pour toute interprétation I, on a I⊨ P si et seulement si I⊨ Q alors que dire que P et Q sont equisatisfiables c’est dire qu’il existe une interprétation I telle que I⊨ P si et seulement si il existe une interprétation J telle que J⊨ Q. Deux formules équivalentes sont equisatisfiables mais le contraire n’est pas vrai.

Le principe de la décomposition est le suivant. On part d’une formule P qui est en forme normale de négation et qui ne contient que des conjonctions et des disjonctions.

On construit un ensemble de clauses, clause(P), tel que : si clause(P) est vraie pour une interprétation I alors P est aussi vraie pour cette interprétation et si P est vraie pour une interprétation I alors il existe une interprétation J qui coincide avec I sur les variables de P et pour laquelle clause(P) est vraie.

Exemple 5 Soit la formule P définie comme (a₁ ∧ b₁) ∨ (a₂ ∧ ¬ b₂) ∨ (¬ a₃ ∧ (b₃ ∨ c)) ∨ a₄ ∨ ¬ b₄. On introduit les variables x₁, x₂ et x₃ pour représenter respectivement (a₁ ∧ b₁) (x₁), (a₂ ∧ ¬ b₂) (x₂), et (¬ a₃ ∧ (b₃ ∨ c)) pour (x₃). L’ensemble des clauses contient

{x₁ ∨ x₂ ∨ x₃ ∨ a₄ ∨ ¬ b₄, ¬ x₁ ∨ a₁, ¬ x₁ ∨ b₁, ¬ x₂ ∨ a₂, ¬ x₂ ∨ ¬ b₂, ¬ x₃ ∨ a₃, ¬ x₃ ∨ b₃ ∨ c }

Preuve: Pour montrer que la transformation est correcte, il suffit de montrer que P est vraie pour une interprétation I si et seulement si clause(P) est vraie pour une interprétation J.

On suppose donnée une interprétation I telle que I⊨ P. On construit une interprétation J qui coincide avec I sur les variables de P et telle que J⊨ clause(P). Le seul cas intéressant est celui dans lequel on introduit une nouvelle variable propositionnelle. Il suffit de montrer que si I⊨ A ∨ (R ∧ Q) et que x est une variable propositionnel qui n’apparaît pas dans A ∨ (R ∧ Q) alors il existe une interprétation J telle que J⊨ A ∨ x, ¬ x ∨ R, ¬ x ∨ Q.

On suppose que I⊨ A ∨ (R ∧ Q), on construit une interprétation J qui coincide avec I pour tous les symboles dans I et on choisit pour interpréter la variable x, la valeur de R∧ Q dans I. Si I⊨ R alors J⊨ R (car I et J coincident sur les symboles qui apparaissent dans R) et a fortiori J ⊨¬ x ∨ R. Si R est faux dans I alors I⊨ ¬ (R∧ Q) et donc x vaut F dans J et donc J⊨¬ x ∨ R. Le même raisonnement s’applique à la clause ¬ x ∨ Q.

Dans l’autre sens, si une interprétation J rend vraie les trois formules {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q}, on va montrer que J⊨ A ∨ (R ∧ Q). Si J⊨ A alors J⊨ A ∨ (R ∧ Q). Sinon comme J⊨ A ∨ x, on en déduit J⊨ x et donc comme J⊨ ¬ x ∨ R et J⊨ ¬ x ∨ Q, on en déduit que J⊨ R et J⊨ Q et donc J⊨ A ∨ (R∧ Q). □

3.1.4 Skolémisation

Les transformations précédentes, traitent de la partie propositionnelle des formules (sans quantificateur), nous allons dans cette section montrer comment peut se traiter la partie avec quantificateurs.

Forme prénexe

Dans la section 2.3.2 nous avons établit des propriétés d’équivalence qui permettent de ramener les quantificateurs en tête de formule. Si x n’est pas libre dans la formule A alors :

Attention la remontée des quantificateurs au travers d’une négation change le quantificateur (loi de de Morgan) de même lorsqu’il est dans la partie gauche d’une implication. La remontée des quantificateurs doit se faire après avoir mis la formule en frme normale de négation.

Proposition 7 (Forme prénexe) Toute formule logique P est équivalente à une formule de la forme

Q x₁, …, Q x_n, A

avec Q l’un des quantificateurs ∀ ou ∃ et A une formule propositionnelle (sans quantificateur). Une formule de la forme Q x₁, …, Q x_n, A est dite en forme prénexe.

Preuve: On commence par mettre la formule P en forme normale de négation puis on utilise les équivalences rappelées ci-dessus pour remonter les quantificateurs en veillant à renommer si nécessaire les variables liées pour ne pas créer de phénomène de capture. Par exemple si on a une formule de la forme A ∨ ∃ x,G(x) et que x est libre dans A (en plus d’être liée dans ∃ x,G(x) alors on commence par renommée la variable liée (ce qui ne change pas le sens de la formule) en choisissant une variable z qui n’est pas libre dans A ni dans ∃ x,G(x), on a alors A ∨ ∃ x,G(x)≡ A ∨ ∃ z,G(z)≡ ∃ z,A ∨ G(z) □

La forme prénexe n’est pas unique. L’ordre des quantificateurs en particulier peut varier en fonction de l’ordre dans lequel on choisit de les faire remonter.

Elimination des quantificateurs existentiels

On a vu qu’intervertir un quantificateur exitentiel et un quantificateur universel en général ne préservait pas l’équivalence entre les formules. Nous allons montrer ici que si on ne s’intéresse qu’à la satisfiabilité, alors on peut se ramener à une formule prénexe qui n’aura que des quantificateurs universels.

La skolemisation est une opération (introduite par le logicien norvégien Thoraf Albert Skolem au 20ème siècle) qui permet de se débarrasser des quantifications existentielles en enrichissant les signatures et en préservant la satisfiabilité des formules.

L’idée de base est que si on s’intéresse à la formule ∀ x,∃ y,P(x,y) cette formule est vérifiée si pour tout élément d du domaine, on peut trouver un élément e du domaine tel que I,{x↦ d,y↦ e}⊨ P(x,y) est vraie. En général, la valeur e retenue pour y dépend de la valeur d choisie pour x. On peut exprimer e en fonction de d et donc le problème ∀ x,∃ y,P(x,y) est analogue au problème ∀ x,P(x,f(x)) dans lequel f est un nouveau symbole de fonction.

De manière plus précise on peut prouver ∀ x,P(x,f(x))⊨ ∀ x,∃ y,P(x,y) et si la formule ∀ x,∃ y,P(x,y) est satisfiable alors on peut à partir d’un modèle de cette formule, trouver un modèle de la formule ∀ x,P(x,f(x)) en choisissant la bonne interprétation pour la fonction f.

Définition 5 (Elimination d’un quantificateur existentiel) Soit une formule A dans laquelle apparaît une sous-formule ∃ y,B. On suppose qu’il y a n variables libres dans ∃ y,B, c’est-à-dire VL(∃ y,B)={x₁,…,x_n}. On introduit alors dans la signature un nouveau symbole de fonction f à n arguments (si n=0 alors f est juste une constante). On introduit la formule A′ qui est la formule A dans laquelle on a remplacé la sous-formule ∃ y,B par B[y← f(x₁,…,x_n)].

Pour que cette opération soit licite il suffit que les variables x₁,…,x_n ne soient pas liées dans B ce qui peut toujours être garanti quite à effectuer des renommages de variables liées dans B.

Proposition 8 Soit A une formule en forme normale de négation. Soit A′ obtenue à partir de A en éliminant un quantificateur existentiel suivant la procédure précédente. On a alors A′⊨ A et tout modèle de A peut être transformé en un modèle de A′ qui coincide avec celui de A sauf pour l’interprétation du nouveau symbole f.

Preuve: La première propriété est une conséquence de B[y← f(x₁,…,x_n)]⊨ ∃ y,B et du fait que A est en forme normale de négation. En effet on vérifie aisément les propriété de stabilité de la conséquance logique : si Q⊨ R alors pour n’importe quelle formule P on a

Pour la seconde propriété on suppose construit un modèle I de la formule A. La formule B a comme variables libres les variables x₁… x_n, y. On regarde dans le modèle l’ensemble des n+1-uplets (d₁,…,d_n,e) tels que I,{x₁↦ d₁,…,x_n↦ d_n,y↦ e}⊨ B. On peut à partir de cette relation construire une fonction f_J ∈ Dⁿ→ D telle que I,{x₁↦ d₁,…,x_n↦ d_n,y↦ f_J(d₁,…,d_n)}⊨ B s’il existe e tel que I,{x₁↦ d₁,…,x_n↦ d_n,y↦ e}⊨ B et f_J(d₁,…,d_n)=d avec d une valeur arbitraire de D si pour tout e, I,{x₁↦ d₁,…,x_n↦ d_n,y↦ e}⊭B. On peut alors construire une interprétation J sur le même domaine D que I, qui étend l’interprétation I avec l’interprétation du symbole de fonction f comme la fonction f_J.

Cette interprétation rend vraie la formule (∃ y,B) ⇔ B[y← f(x₁,…,x_n)] pour tout environnement {x₁↦ d₁,…,x_n↦ d_n}. Elle rend donc aussi vraie la formule ∀ x₁… x_n,((∃ y,B) ⇔ B[y← f(x₁,…,x_n)]). Par ailleurs cette interprétation rend vraie la formule A car J est une extension de I qui est un modèle de A. Comme par ailleurs on peut montrer ∀ x₁ … x_n,((∃ y,B) ⇔ B[y← f(x₁,…,x_n)]) ⊨ A⇔ A′ car A′ est obtenue à partir de A en remplaçant ∃ y,B par B[y← f(x₁,…,x_n)], on en déduit que J est un modèle de A′. □

On peut itérer l’opération précédente pour éliminer tous les quantificateurs existentiels d’une formule. Chaque élimination de quantificateur introduit un nouveau symbole de fonction.

Si on applique ces transformations à une formule A en forme normale de négation, on obtient une formule B sans quantificateur existentiel telle que

Proposition 9 Soit A une formule en forme normale de négation et B une formule obtenue par élimination des quantificateurs existentiels de A.

Si B est valide alors A l’est aussi.
Si B est satisfiable alors A l’est aussi.
Si B est insatisfiable alors A l’est aussi.

Preuve: Les deux premières propriétés sont des conséquences directes de B⊨ A alors que la dernière vient du fait que s’il existait un modèle de A alors il y en aurait aussi un de B. □

Exemple 6 Soit la formule (∃ x,∀ y,P(x,y)) ∧ (∃ z,∀ u,¬ P(u,z)) on obtient la formule suivante avec a et b des nouvelles constantes et (∀ y,P(a,y)) ∧ (∀ u,¬ P(u,b)). Cette formule est satisfiable, par contre si on avait utilisé deux fois la même constante a on aboutirait à une formule insatisfiable.

Proposition 10 (Skolemisation) Soit A une formule close alors il existe une formule B en forme normale négative qui ne contient que des connecteurs ∧ et ∨ et pas de quantificateur existentiel ou universel telle que si VL(B)={x₁,…,x_n} on a

∀ x₁ … x_n, B ⊨ A
si A a un modèle alors il en est de même de ∀ x₁… x_n, B

Preuve: Il suffit d’éliminer les symboles d’implication et mettre la formule en forme normale négative. On applique ensuite l’élimination des quantificateurs existentiels suivant la procédure vue précédemment. On fait ensuite remonter les quantificateurs universels (en s’assurant au préalable qu’il n’y en n’a pas deux différents qui portent sur une variable de même nom) et en utilisant les équivalences A ∘ ∀ x, B ≡ ∀ x, (A ∘ B) lorsque x n’est pas libre dans B et ∘ ∈ {∨,∧}. Une fois que tous les quantificateurs universels sont en tête (c’est-à-dire que la formule est en forme prénexe) il suffit de les éliminer pour obtenir la formule skolemisée. □

Cette opération peut nous permettre de montrer la validité d’une formule. En effet la validité d’une formule A est équivalent à l’insatisfiabilité de la formule ¬ A qui se ramène donc à l’insatisfiabilité de la forme skolémisée de ¬ A. Comme la forme skolémisée est une formule universelle, le théorème de Herbrand nous permet de ramener la satisfiabilité à l’existence d’un modèle construit sur le domaine de Herbrand.

Exemple 7 On part de la formule A =^def (∀ x, (P(x) ⇒ Q(x))) ⇒ (∀ x, P(x)) ⇒ ∀ x, Q(x) et on skolemise ¬A

Forme normale négative : (∀ x, (¬ P(x) ∨ Q(x))) ∧ (∀ y, P(y)) ∧ ∃ z,¬ Q(z)
Elimination du quantificateur existentiel : (∀ x, (¬ P(x) ∨ Q(x))) ∧ (∀ y, P(y)) ∧ ¬ Q(a)
Mise en forme prénexe : ∀ x y, ((¬ P(x) ∨ Q(x))∧ P(y) ∧ ¬ Q(a))
Elimination des quantificateurs universels : (¬ P(x) ∨ Q(x)) ∧ P(y) ∧ ¬ Q(a)

Cette formule n’est pas vraie dans l’environnement {x↦ a,y↦ a} donc la formule ∀ x y, ((¬ P(x) ∨ Q(x))∧ P(y) ∧ ¬ Q(a)) est fausse dans toute interprétation de Herbrand, elle est donc insatisfiable et donc il en est de même de la formule ¬ A donc A est valide.

Définition 6 (Fermeture universelle) Soit P une formule dont les variables libres sont { x₁,…, x_n}. On appelle fermeture universelle de la formule P et on notera ∀(P) la formule ∀ x₁,…, x_n,P. Cette formule est cloase (sans variable libre). L’opération de permutation de deux quantificateurs universels ne change pas le sens de la formule donc l’ordre dans lequel les variables apparaissent dans les quantificateurs n’a pas d’importance.

Skolemisation d’un ensemble de formules.

Si on se donne un ensemble de formules A₁,…,A_n on peut traiter la skolémisation de manière indépendante pour chaque formule. On obtient pour chaque A_i une formule B_i sans quantificateurs telle que ∀(B_i)⊨ A_i. On en déduit aisément que :

Forme clausale d’une formule avec quantificateur

Définition 7 (Forme clausale d’une formule avec quantificateur) La forme clausale d’une formule P est un ensemble de clauses C={C₁,…,C_p}. Cet ensemble de clauses s’obtient en construisant la forme de skolem de la formule P qui s’écrit ∀ x₁ … x_n, A avec A formule propositionnelle. L’ensemble de clauses C={C₁,…,C_p} est ensuite obtenu en mettant en forme normale conjonctive la formule A. On a alors

C₁,…,C_p ⊨ A
∀(C₁),…,∀(C_p)⊨ P
S’il existe un modèle de P alors on peut l’étendre en un modèle des formules ∀(C₁),…,∀(C_p).

Exercice 2 On part de la formule A =^def (∃ x, ∀ y, R(x,y)) ⇒ (∀ y, ∃ x, R(x,y)).

Donner la forme normale de négation de la formule ¬ A
Donner la forme de skolem de la formule ¬ A
Donner la forme clausale de ¬ A
la formule ¬ A est-elle satisfiable ? La formule A est-elle valide ?

Chapitre 3 Manipuler les formules de la logique