Personal page of Benjamin Hellouin

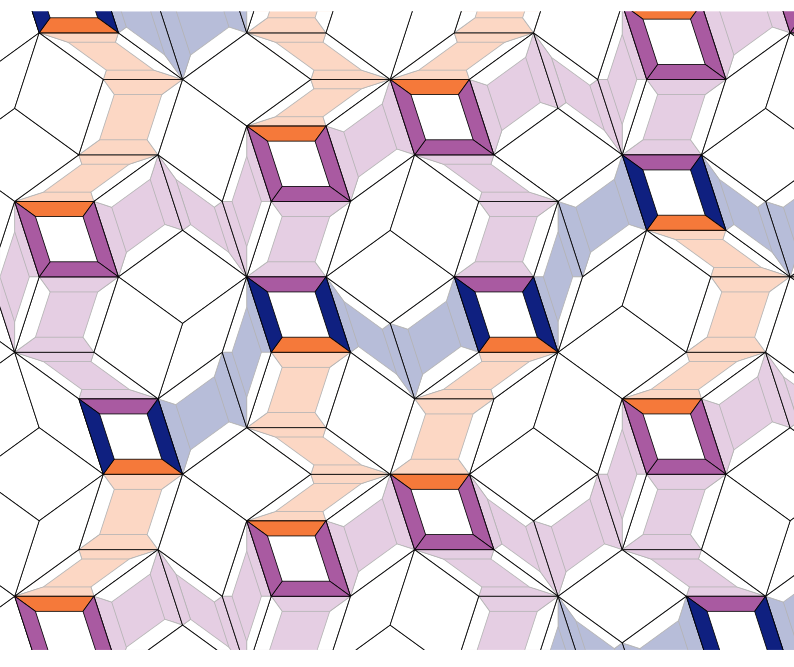
Geometric tilings consist in covering the Euclidean plane using copied of a set of tiles, typically polygons. The word "geometric" is to contrast with "symbolic" tilings, where constraints are given by forbidden patterns (on colours or symbols) rather than the geometry of the tiles.

In C8, we study the classical Domino problem in a mixed context. Underling geometric constraints are given in advance, symbolic constraints (colouring of the tiles) are given as input, and we have to decide whether it is possible to tile the plane while satisfying all contraints. We show that the problem remains undecidable when tiles are rhombi, just as in the classical case (corresponding to a single square tile), regardless of the underlying geometric constraints.

A substitution is a word tranformation that consists in replacing every letter by a word ($a\to ab, b\to a$). Fixed points or limit points of substitutions or, more generally, of sets of substitutions (S-adic systems), are infinite words that receive a lot of interest for their dynamical and combinatorial properties. Sturmian words are a typical example.

In C7, we study the conditions under which a finite automata (or a sofic subshift) may or may not accept an infinite word given in this way. We devise algorithms based on the notion of automata desubstitution to decide this problem in most cases, and provide some combinatorial results about their structure.

Hom shifts are a class of simple tilings defined by adjacency conditions that are the same in every direction, so that they can be described by a finite undirected graph on the set of colors. This class includes well-known and much-studied models such as k-colourings, the square ice and the hard square models.

In S, we study mixing properties of these tilings, that is, how far from each other two patterns need to be so that they can be completed into a valid tiling. It turns out that there is a transition between logarithmic and linear behaviours that depends on the algebraic and topological properties of the graph.

A configuration on a finitely generated group is a coloring of the Cayley graph associated with the group by a finite set of symbols, generalising the usual cases on Z and Z^2. Since the Cayley graph is regular (an inbound edge and an outbound edge by generator), one can define restrictions on allowed neighbouring symbols, for example using Wang tiles. A set of such restrictions defines a subshift on the group.

It is interesting to note that a given set of restrictions can apply to all groups with the same number of generators, and defines a subshift on each such group. In addition to studying individual subshifts, we can study the relationship between subshifts on the different groups to find global properties.

In J7, we study two known conditions on subshifts of Z^2 and of the free group. We show that these conditions are equivalent and necessary for the existence of a configuration on any amenable groupe.

Almost all classical undecidability results on subshifts of finite type of higher dimension rely on the existence of aperiodic points, a phenomenon that shaped this research area.

In C5, we show that any aperiodic point of a Z^2-subshift have a certain structure that describes the distance between locations where the different periods are broken. This lets us characterise the degree of undecidability of the problem of deciding whether a subshift has an aperiodic point, and to describe the properties of Z^2-subshifts with no aperiodic points.

In C6, we prove that this phenomenon no longer occurs in dimension 4 and more, and that the degree of undecidability of the above problem is much higher (outside of the arithmetical hierarchy). Such difficulty gaps are unusual above dimension 2.

The 3-dimensional case is open and we are still working on it (with Antonin Callard and Ville Salo).

The entropy of a subshift is a real parameter that corresponds to the exponential growth rate of the number of admissible finite patterns. Given a subshift of finite type, computing its entropy is a well-studied problem which was solved on a few rare examples. It is often very difficult and undecidable in the general case.

In J6, we study how the difficulty of the problem changes depending on a parameter that represents a mixing rate for the subshift. In a more general class, decidable subshifts, we characterise the threshold where the problem go from decidable to undecidable. We conjecture this threshold also holds for subshifts of finite type.

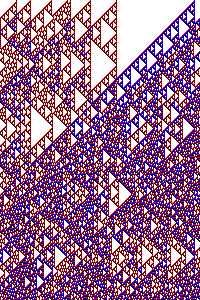
A family of cellular automata exhibit a phenomenon called randomisation that can be described as follows. Draw an random initial configuration according to an arbitrary probability measure and iterate the cellular automaton on this configuration. As the number of iteration (time) tends to infinity, the pattern that appear at any given place tends to be distributed among all possible patterns with equal probability.

Automata for which this phenomenon is best-understood are the abelian cellular automata, that is, the endomorphisms when the alphabet is endowed with a commutative group structure. Proofs are generally base on Fourier analysis.

In J5, we characterise abelian cellular automata that exhibit this behaviour in Cesàro mean convergence by an elementary combinatorial property, which generalises most existing results in this context. Moreover, we provide an example of randomisation in direct convergence, a phenomenon which had never been formally proven before.

Langton's insects are a family of Turing machines working on two-dimensional tapes with simple rules: the tape alphabet is Z/nZ; when the insect visits a cell, it increments the letter and turns by an angle given by the letter and the insect's rule, and goes forward by one step.

Despite their simplicity, those models exhibit complex dynamical behaviours. Starting from a simple configuration - say, uniform - they have highly irregular trajectories, apparently disordered and chaotic with some transitory symmetries. Some of them converge to a periodic behaviour after a very long time, which is the object of Langton's conjecture.

J4, which is mostly Diego Maldonado's master thesis work, show that the family of Turmites is able to embed universal computation (through simulating a cellular automaton), the input being written in a finite part of an otherwise periodic initial configuration. This lets us show the P-completeness of a prediction problem for those models, the same situation as the classical ones.

Self-organisation is the emergence of a structured behaviour from a simple or random initial configuration. In cellular automata, it often takes the form of growing regions consisting of a simple repeated pattern separated by borders that evolve at constant speed and interact as particles. Thus, tools from interacting particle systems and random walks can be used to describe the typical behaviour of the automaton.

This study can be roughly decomposed into two steps:

1. Identify and describe the particles, understand and prove the relationship with the corresponding particle system;
2. Obtain qualitative and quantitative results on this system and understand their consequences on the behaviour of the automaton.

In J3, which contains and generalises C2 and C3, we define a framework and tools to perform this study in arbitrary cellular automata. For example, we provide results that determine which particles survive asymptotically and the speed of convergence to the limit measure in some cases.

In S, we consider the so-called 3-state cyclic cellular automaton whose states are in a "rock-paper-scissors" relationship. This automaton is a simple example of a particle system and also used as a toy model, for example in population dynamics. We determine the asymptotic behaviour starting from an independant nonuniform initial measure, and observe a paradoxal behaviour of "survival of the weakest".

When an initial configuration is drawn at random - say, uniformly - what variety and complexity can we expect to see by iterating cellular automata on this condiguration? A way to handle this question is to consider limit measures, which are a description of typical asymptotic behaviour. Which limit measures are reachable by cellular automata is also a description of the computational power of this (probabilistic) model of computation.

In the following works, we completely characterise reachable limit measures by computability conditions. Formally, we show that hey are exactly the semi-computable measures, the same situation as for Turing machines.

J1 provides a construction for dimension 1. J2, which extends and generalises C4, introduces a more complex construction that gives the same result for higher dimensions.

Counting matchings or perfect matchings in graphs is a difficult problem: #P-complete in the general case. It remains difficult in many subclasses, but there are some polynomial-time algorithms obtained by bounding a parameter called clique-width.

In C1, we enrich existing methods to count maximal matchings and some other extensions. The algorithm runs in time O(n^poly(k)) where k is the clique-width.

This article is the result of an M1 internship.