Depuis septembre 2017, je suis maître de conférences dans l'équipe GaLAC (Graphes, Algorithmes, Combinatoire) au Laboratoire de Recherche en Informatique (LRI), université Paris-Sud. J'enseigne au département Informatique de l'Institut Universitaire de Technologie (IUT) d'Orsay.
La plupart des documents sur ce site ont été réalisés lorsque j'étais payé par l'État français (ou chilien). J'autorise et j'encourage chacun à réutiliser librement leur contenu. Pour toute question ou commentaire, ou si vous avez besoin d'une source tex :
- hellouin [at] lri [point] fr pour la recherche ;
- benjamin.hellouin-de-menibus [at] u-psud [point] fr pour l'enseignement.
Enseignement
J'enseigne dans le département informatique de l'IUT d'Orsay.
Je suis responsable (depuis 2017) du cours CODIN, ou « Conception de documents et d'interfaces numériques » (code PPN : M1105) en première année. La matériel de cours utilisé en 2019-2020 :
- Le polycopié du cours et le planning général
- Le TP1 (avec sa feuille d'aide et un exemple), le TP2 (avec sa feuille d'aide et un exemple), Le TP3 (avec sa feuille d'aide et un exemple)
- Le projet final et son barême.
Un rassemblement de vieux matériel pédagogique :
- Quelques développements pour l'agrégation de mathématiques, option informatique. Aucune garantie de qualité.
- Cours de calcul vectoriel donné en espagnol à la Universidad Andrés Bello. Le matériel a été crée en coopération par Daniel Pons Rubio et l'équipe pédagogique.
Sujets de recherche
Ma recherche concerne les systèmes dynamiques, spécifiquement la dynamique symbolique (en particulier les automates cellulaires et les pavages / sous-décalages). Mes sujets impliquent en général la théorie de la calculabilité (pour l'aspect informatique) et/ou la théorie ergodique et les probabilités discrètes (pour l'aspect mathématique).
Mes directions de recherche principales sont:
- Calculabilité dans les systèmes dynamiques, interaction entre dynamique et capacité à simuler du calcul, et la difficulté de calculer divers objets dynamiques ;
- Probabilités discrètes et auto-organisation, étudiés par des outils probabilistes tels que des systèmes de particules en interaction.
Publications
Les publications ci-dessous sont classées thématiquement, par ordre antichronologique (approximatif) de mon travail sur chaque thème. Les publication en conférences (C) et en journaux (J) sont numérotées par ordre de fin rédaction, qui n'est pas forcément celui de publication.
Cliquez sur le nom de chaque thème pour un résumé.
Sous-décalages / Pavages
Un pavage d'un groupe finiment généré est une assignation d'un symbole à chaque sommet du graphe de Cayley associé au groupe, une généralisation des cas classiques Z et Z^2. Comme le graphe de Cayley est régulier (une arête sortante et une entrante par générateur), on peut définir des restrictions sur les symboles voisins autorisés de manière uniforme, par exemple en utilisant des tuiles de Wang. Un ensemble de telles restrictions définit un sous-décalage sur ce groupe.
Il est intéressant de noter qu'un jeu de restrictions donné fonctionne pour tous les groupes ayant le bon nombre de générateurs, et définit un sous-décalage sur chacun de ses groupes. En plus d'étudier les sous-décalages individuels, on peut étudier la relation entre ces sous-décalages et chercher des propriétés globales.
Dans J8, nous étudions deux conditions connues sur les sous-décalages de Z^2 et du groupe libre. Nous montrons que ces deux conditions sont équivalentes et nécessaires pour l'existence d'un pavage sur tout groupe moyennable.
Un pavage d'un groupe finiment généré est une assignation d'un symbole à chaque sommet du graphe de Cayley associé au groupe, une généralisation des cas classiques Z et Z^2. Comme le graphe de Cayley est régulier (une arête sortante et une entrante par générateur), on peut définir des restrictions sur les symboles voisins autorisés de manière uniforme, par exemple en utilisant des tuiles de Wang. Un ensemble de telles restrictions définit un sous-décalage sur ce groupe.
Il est intéressant de noter qu'un jeu de restrictions donné fonctionne pour tous les groupes ayant le bon nombre de générateurs, et définit un sous-décalage sur chacun de ses groupes. En plus d'étudier les sous-décalages individuels, on peut étudier la relation entre ces sous-décalages et chercher des propriétés globales.
Dans J8, nous étudions deux conditions connues sur les sous-décalages de Z^2 et du groupe libre. Nous montrons que ces deux conditions sont équivalentes et nécessaires pour l'existence d'un pavage sur tout groupe moyennable.
Necessary conditions for tiling finitely generated amenable groups
Publié à Discrete and Continuous Dynamical Systems, 2020
[publication, arXiv, HAL, bibtex]
Sous-décalages / Pavages
Décidabilité / Calculabilité

Presque tous les résultats classiques d'indécidabilité dans les sous-décalages de type fini de dimension >1 reposent sur l'existence de points apériodiques, un phénomène qui a donné sa forme actuelle à ce domaine de recherche.
Dans C5, nous démontrons que tout point apériodique d'un sous-décalage de Z^2 dispose d'une certaine structure qui décrit la distance entre les lieux où la périodicité est brisée. Cela nous permet de caractériser le niveau d'indécidabilité du problème de décider si un sous-décalage possède un point apériodique, et de décrire des propriétés des sous-décalages de Z^2 sans point apériodique.
Ce que devient cette structure et toutes ces autres questions restent ouvertes en dimension 3 et plus.
Presque tous les résultats classiques d'indécidabilité dans les sous-décalages de type fini de dimension >1 reposent sur l'existence de points apériodiques, un phénomène qui a donné sa forme actuelle à ce domaine de recherche.
Dans C5, nous démontrons que tout point apériodique d'un sous-décalage de Z^2 dispose d'une certaine structure qui décrit la distance entre les lieux où la périodicité est brisée. Cela nous permet de caractériser le niveau d'indécidabilité du problème de décider si un sous-décalage possède un point apériodique, et de décrire des propriétés des sous-décalages de Z^2 sans point apériodique.
Ce que devient cette structure et toutes ces autres questions restent ouvertes en dimension 3 et plus.
Aperiodic points in Z^2-subshifts.
Publié à ICALP, 2018.
[publication, arXiv, HAL, bibtex]
Sous-décalages / Pavages
Décidabilité / Calculabilité

L'entropie d'un sous-décalage est un paramètre réel qui correspond au taux de croissance exponentiel du nombre de motifs admissibles. Étant donné un sous-décalage de type fini, calculer son entropie est une question bien étudiée. Quelques rares exemples non triviaux ont été résolus, mais ce problème se révèle très difficile et indécidable dans le cas général.
Dans J, nous étudions la manière dont la difficulté de ce problème évolue lorsque l'on fait varier un paramètre qui représente le taux de mélange du sous-décalage. Dans une classe plus générale, les sous-décalages décidables, nous caractérisons exactement le seuil auquel le problème passe de décidable à indécidable. Nous conjecturons que ce seuil est le même pour les sous-décalages de type fini.
L'entropie d'un sous-décalage est un paramètre réel qui correspond au taux de croissance exponentiel du nombre de motifs admissibles. Étant donné un sous-décalage de type fini, calculer son entropie est une question bien étudiée. Quelques rares exemples non triviaux ont été résolus, mais ce problème se révèle très difficile et indécidable dans le cas général.
Dans J, nous étudions la manière dont la difficulté de ce problème évolue lorsque l'on fait varier un paramètre qui représente le taux de mélange du sous-décalage. Dans une classe plus générale, les sous-décalages décidables, nous caractérisons exactement le seuil auquel le problème passe de décidable à indécidable. Nous conjecturons que ce seuil est le même pour les sous-décalages de type fini.
Effect of quantified irreducibility on the computability of subshift entropy.
Publié dans Discrete and Continuous Dynamical Systems, 2019.
[publication, arXiv, HAL, bibtex]
Automates cellulaires
Comportement en moyenne
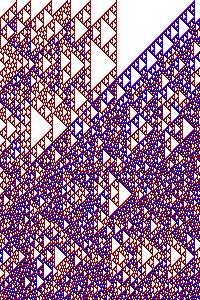

Une famille d'automates cellulaires - aux contours encore mal connus - présente un phénomène, dit de randomisation, qu'on peut décrire comme suit. Tirons une configuration initiale au hasard, suivant une mesure de probabilité arbitraire, et itérons l'automate cellulaire sur cette configuration. Comme le nombre d'itérations (le temps) tend vers l'infini, le motif qui apparaît à un endroit donné tend à être n'importe quel motif possible avec égale probabilité.
Les automates sur lesquels ce phénomène est le mieux compris sont les automates cellulaires abéliens, c'est-à-dire correspondant à un endomorphisme quand l'alphabet est muni d'une structure de groupe commutatif. Les preuves sont fondées le plus souvent sur l'analyse de Fourier.
Dans J, nous caractérisons les automates cellulaires abéliens qui présentent ce comportement pour la convergence en moyenne par une propriété combinatoire simple, ce qui généralise la plupart des résultats existant pour ce contexte. De plus, nous montrons un exemple où la convergence se fait de manière directe, ce dont il n'existait pas de preuve formelle auparavant.


Une famille d'automates cellulaires - aux contours encore mal connus - présente un phénomène, dit de randomisation, qu'on peut décrire comme suit. Tirons une configuration initiale au hasard, suivant une mesure de probabilité arbitraire, et itérons l'automate cellulaire sur cette configuration. Comme le nombre d'itérations (le temps) tend vers l'infini, le motif qui apparaît à un endroit donné tend à être n'importe quel motif possible avec égale probabilité.
Les automates sur lesquels ce phénomène est le mieux compris sont les automates cellulaires abéliens, c'est-à-dire correspondant à un endomorphisme quand l'alphabet est muni d'une structure de groupe commutatif. Les preuves sont fondées le plus souvent sur l'analyse de Fourier.
Dans J, nous caractérisons les automates cellulaires abéliens qui présentent ce comportement pour la convergence en moyenne par une propriété combinatoire simple, ce qui généralise la plupart des résultats existant pour ce contexte. De plus, nous montrons un exemple où la convergence se fait de manière directe, ce dont il n'existait pas de preuve formelle auparavant.
Characterizing Asymptotic Randomization in Abelian Cellular Automata.
Publié dans Ergodic Theory and Dynamical Systems, 2020.
[publication, arXiv, HAL, bibtex]
Modèle de calcul
Décidabilité / Calculabilité

Les insectes de Langton sont une famille de machines de Turing sur ruban 2D à règles simples : l'alphabet du ruban est Z/nZ ; quand l'insecte visite une case, il incrémente la lettre lue et tourne d'un angle qui dépend la lettre lue et de la règle de l'insecte.
En dépit de leur simplicité, ces modèles présentent des dynamiques complexes. Partant d'une configuration simple - uniforme par exemple - ils présentent des trajectoires irrégulières, apparemment désordonnées et chaotiques avec certaines symétries passagères. Certains modèles convergent vers un comportement périodique après un temps très long, ce qui est l'objet de la conjecture de Langton.
J, qui est principalement le travail de thèse de master de Diego Maldonado, nous montre que la famille des Turmites est capable de calcul universel (simulation d'un automate cellulaire), l'entrée étant écrite sur une partie finie d'une configuration initiale périodique. Cela nous permet de montrer la P-complétude d'un problème de prédiction pour ces modèles, comme c'est le cas pour les modèles de calcul classique.

Les insectes de Langton sont une famille de machines de Turing sur ruban 2D à règles simples : l'alphabet du ruban est Z/nZ ; quand l'insecte visite une case, il incrémente la lettre lue et tourne d'un angle qui dépend la lettre lue et de la règle de l'insecte.
En dépit de leur simplicité, ces modèles présentent des dynamiques complexes. Partant d'une configuration simple - uniforme par exemple - ils présentent des trajectoires irrégulières, apparemment désordonnées et chaotiques avec certaines symétries passagères. Certains modèles convergent vers un comportement périodique après un temps très long, ce qui est l'objet de la conjecture de Langton.
J, qui est principalement le travail de thèse de master de Diego Maldonado, nous montre que la famille des Turmites est capable de calcul universel (simulation d'un automate cellulaire), l'entrée étant écrite sur une partie finie d'une configuration initiale périodique. Cela nous permet de montrer la P-complétude d'un problème de prédiction pour ces modèles, comme c'est le cas pour les modèles de calcul classique.
Nontrivial Turmites are Turing-universal.
Publié dans Journal of Cellular Automata, 2018.
[publication, arXiv, bibtex]
Automates cellulaires
Comportement en moyenne
Probabilités discrètes

L'auto-organisation correspond à l'émergence d'un comportement structuré à partir d'une configuration initiale simple ou tirée au hasard. Un mécanisme courant d'auto-organisation dans les automates cellulaires consiste en l'apparition de régions contenant en un motif simple répété séparées par des frontières qui évoluent à vitesse constante et interagissent telles des particules. Ainsi, des outils de systèmes de particules en interactions et de marches aléatoires sont utilisés pour décrire le comportement en moyenne de l'automate.
Cette étude peut grossièrement se décomposer en deux étapes :
- Identifier et décrire les particules, comprendre et prouver les relations avec le système de particules correspondant ;
- Prouver des résultats qualitatifs et quantitatifs sur ces systèmes et comprendre leur conséquence sur le comportement de l'automate.
Dans J3, qui rassemble et généralise C2 et C3, nous définissons un cadre et des outils généraux pour effectuer cette étude dans des automates cellulaires quelconques. Par exemple, nous fournissons des résultats pour déterminer quelles particules survivent asymptotiquement et la vitesse de convergence à la mesure limite dans certains cas.
Dans S, nous considérons un automate cellulaire dit cyclique à trois états en relation de « pierre-papier-ciseaux ». Cet automate est un exemple simple de système de particules également utilisé comme modèle-jouet, par exemple en dynamique des populations. Nous déterminons le comportement asymptotique partant d'une mesure initiale indépendante non uniforme, qui présente un comportement paradoxal de « survie du plus faible ».

L'auto-organisation correspond à l'émergence d'un comportement structuré à partir d'une configuration initiale simple ou tirée au hasard. Un mécanisme courant d'auto-organisation dans les automates cellulaires consiste en l'apparition de régions contenant en un motif simple répété séparées par des frontières qui évoluent à vitesse constante et interagissent telles des particules. Ainsi, des outils de systèmes de particules en interactions et de marches aléatoires sont utilisés pour décrire le comportement en moyenne de l'automate.
Cette étude peut grossièrement se décomposer en deux étapes :
- Identifier et décrire les particules, comprendre et prouver les relations avec le système de particules correspondant ;
- Prouver des résultats qualitatifs et quantitatifs sur ces systèmes et comprendre leur conséquence sur le comportement de l'automate.
Dans J3, qui rassemble et généralise C2 et C3, nous définissons un cadre et des outils généraux pour effectuer cette étude dans des automates cellulaires quelconques. Par exemple, nous fournissons des résultats pour déterminer quelles particules survivent asymptotiquement et la vitesse de convergence à la mesure limite dans certains cas.
Dans S, nous considérons un automate cellulaire dit cyclique à trois états en relation de « pierre-papier-ciseaux ». Cet automate est un exemple simple de système de particules également utilisé comme modèle-jouet, par exemple en dynamique des populations. Nous déterminons le comportement asymptotique partant d'une mesure initiale indépendante non uniforme, qui présente un comportement paradoxal de « survie du plus faible ».
Asymptotic behaviour of the one-dimensional "Rock-Paper-Scissors" cyclic cellular automaton.
Soumis à Annals of Applied Probability, 2019.
[arXiv, HAL, bibtex]
Self-organisation in cellular automata with coalescent particles: qualitative and quantitative approaches.
Publié dans Journal of Statistical Physics, 2017.
[publication, arXiv, HAL, bibtex]
Entry times in cellular automata with simple defects dynamics.
Publié dans Automata/JAC, 2012.
[publication, arXiv, HAL, bibtex]
Self-organization in cellular automata: a particle-based approach.
Publié dans DLT, 2011.
[publication, manuscrit, bibtex]
Automates cellulaires
Modèle de calcul
Décidabilité / Calculabilité

Quand une configuration initiale est tirée au hasard - disons, uniformément -, quelle variété et quel niveau de complexité peut-on s'attendre à observer en itérant un automate cellulaire sur cette configuration ? Une manière de traiter cette question est de considérer les mesures limites possibles, qui sont une description du comportement asymptotique. Comprendre l'ensemble des mesures limites atteignables par automate cellulaire est aussi une mesure de la puissance calculatoire ce de modèle (probabiliste) de calcul.
Dans les travaux ci-dessous, nous caractérisons complètement les mesures limites possibles par des conditions de calculabilité. Plus formellement, nous montrons qu'il s'agit exactement des mesures semi-calculables, la même situation que pour les machines de Turing.
J1 fournit une construction pour la dimension 1. J2, qui étend et généralise C4, introduit une construction plus complexe qui produit le même résultat pour les dimensions supérieures.
Quand une configuration initiale est tirée au hasard - disons, uniformément -, quelle variété et quel niveau de complexité peut-on s'attendre à observer en itérant un automate cellulaire sur cette configuration ? Une manière de traiter cette question est de considérer les mesures limites possibles, qui sont une description du comportement asymptotique. Comprendre l'ensemble des mesures limites atteignables par automate cellulaire est aussi une mesure de la puissance calculatoire ce de modèle (probabiliste) de calcul.
Dans les travaux ci-dessous, nous caractérisons complètement les mesures limites possibles par des conditions de calculabilité. Plus formellement, nous montrons qu'il s'agit exactement des mesures semi-calculables, la même situation que pour les machines de Turing.
J1 fournit une construction pour la dimension 1. J2, qui étend et généralise C4, introduit une construction plus complexe qui produit le même résultat pour les dimensions supérieures.
Characterisation of limit measures of higher-dimensional cellular automata.
Publié dans Theory of Computing Systems, 2017.
[publication, arXiv, HAL, bibtex]
Construction of mu-limit sets of two-dimensional cellular automata.
Publié dans STACS, 2015.
[publication, manuscrit, bibtex]
Characterization of sets of limit measures of a cellular automaton iterated on a random configuration.
Publié dans Ergodic Theory and Dynamical Systems, 2018.
[publication, arXiv, HAL, bibtex]
GraphesComplexité paramétréeComptage

Compter les couplages ou les couplages parfaits d'un graphe est un problème difficile : #P-complet dans le cas général. Cette difficulté demeure dans beaucoup de sous-classes, mais on dispose de quelques algorithmes en temps polynomial en bornant un paramètre appelé largeur de clique.
Dans C1, nous enrichissons les méthodes existantes pour pouvoir compter les couplages maximaux, et quelques autres extensions. L'algorithme obtenu est en O(n^poly(k)) où k est la largeur de clique.
Il s'agit d'un travail issu d'un stage de M1.
Compter les couplages ou les couplages parfaits d'un graphe est un problème difficile : #P-complet dans le cas général. Cette difficulté demeure dans beaucoup de sous-classes, mais on dispose de quelques algorithmes en temps polynomial en bornant un paramètre appelé largeur de clique.
Dans C1, nous enrichissons les méthodes existantes pour pouvoir compter les couplages maximaux, et quelques autres extensions. L'algorithme obtenu est en O(n^poly(k)) où k est la largeur de clique.
Il s'agit d'un travail issu d'un stage de M1.
Maximal matching and path matching counting in polynomial time for graphs of bounded clique width.
Publié dans TAMC, 2011.
[publication, arXiv, bibtex]
Thèse
J'ai effectué ma thèse, intitulée Comportement asymptotique des automates cellulaires : Aléa et Calcul, sous la direction de Xavier Bressaud et Mathieu Sablik à l'université d'Aix-Marseille. La défense a eu lieu le 26 septembre 2014 à Marseille. Voici le manuscrit.
Encadrement
Voici une liste des étudiants que j'ai encadré en stage.- niveau L3:
- Guillaume Lasnier (guillaume.lasnier [at] universite-paris-saclay [point] fr) pour 3 semaines en 2019.
- Margot Ferré (margot-ferre [at] orange [point] fr) pour 3 semaines en 2019.
- niveau M2:
- Léo Paviet-Salomon (leo.paviet-salomon [at] ens-lyon [point] fr) pour 5 mois en 2020.
CV
Version pdf en français ou en anglais.
- sept. 2017 - actuellement: Maître de conférences dans l'équipe GALaC, LRI, université Paris-Sud.
- sept. 2016 - août 2017: ATER dans l'équipe Automates et Applications, IRIF, université Paris Diderot.
- sept. 2014 - août 2016 : Post-doctorat sous la direction de Cristobal Rojas, Universidad Andrés Bello (Santiago, Chili).
- sept. 2011 - sept. 2014 : Thèse en informatique: Comportement asymptotique des automates cellulaires : aléa et calcul (manuscrit ci-dessous).
Divers & Recommendations
Je suis un fervent joueur de go. Vous pouvez me croiser à l'un des nombreux clubs de Santiago (ICO, Tengen) ou sur KGS (Jhyn).
J'écoute beaucoup de musique depuis peu. Je dois à Emmanuel Jeandel de m'avoir, entre autres, fait découvrir l'excellent site rateyourmusic.
Camarades de souffrance en langues, je recommance Anki, un système flexible multi-plateformes de flashcards.
