


Eléments de logique pour l’informatique 2021–22
Chapitre 3 Manipuler les formules de la logique
Dans ce chapitre, nous allons aborder la logique et les formules sur le plan syntaxique, c’est-à-dire que nous chercherons à établir des propriétés logiques des formules (validité, satisfiabilité) par des transformations sans passer par la notion de modèle. Nous étudierons tout d’abord des mises en formes canoniques de formules logiques et en particulier la mise en forme clausale. Nous introduirons également la représentation des formules propositionnelles comme des diagrammes de décision binaires. Finalement nous introduirons des systèmes de déduction pour les formules et en particulier le calcul des séquents.
3.1 Formes normales
Dans le chapitre 2 nous avons introduit la forme normale de négation d’une formule. Une formule en forme normale de négation ne contient pas de connecteur ⇒ (ou ⇔) et les seules négations portent sur des symboles de prédicat. Grace aux lois de de Morgan, il est possible de propager les symboles de négation jusqu’aux symboles de prédicat et donc toute formule est équivalente à une formule en forme normale de négation. De plus cette transformation ne change pas (l’ordre de grandeur de) la taille de la formule.
3.1.1 Forme normale de négation
Définition 1 (Littéral) On appelle littéral une formule qui est soit une formule atomique, soit de la forme ¬ R(t1,…,tn) avec R un symbole de prédicat.
Dans la suite, on parlera d’instance de prédicat pour désigner une formule atomique R(t1,…,tn) avec R un symbole de prédicat. Une formule atomique est soit une instance de prédicat soit de la forme ⊤ ou ⊥. Dans le cas propositionnel, les instances de prédicat sont juste les variables propositionnelles.
Proposition 1
Toute formule est équivalente à une formule
en forme normale de négation, c’est-à-dire qui ne comporte pas de connecteur
¬ sauf dans un littéral et n’utilise que les connecteurs ⊤,⊥,∨ et ∧ et les quantificateurs ∀ et ∃.
Preuve:
Pour définir un algorithme qui calcule la forme normale de négation d’une formule, on construit deux fonctions de manière récursive :
fnn qui étant donnée une
formule quelconque P, construit une formule en forme normale
de négation équivalente à P et neg qui étant donnée une
formule quelconque P, construit une formule en forme normale
de négation équivalente à ¬ P.
|
| | fnn(p) | = p | si p atomique |
| fnn(¬ A) | = neg(A) |
| fnn(A∘ B) | = fnn(A)∘ fnn(B) | ∘ ∈ {∨,∧} |
| fnn(A⇒ B) | = neg(A)∨ fnn(B) |
| fnn(∀ x,A) | = ∀ x,fnn(A) |
| fnn(∃ x,A) | = ∃ x,fnn(A) |
| neg(⊤) | = ⊥ |
| neg(⊥) | = ⊤ |
| neg(R(t1,…,tn)) | = ¬ R(t1,…,tn) | R symbole de prédicat |
| neg(¬ A) | = fnn(A) |
| neg(A ∧ B) | = neg(A) ∨ neg(B) |
| neg(A ∨ B) | = neg(A) ∧ neg(B) |
| neg(A ⇒ B) | = fnn(A) ∧ neg(B) |
| neg(∀ x,A) | = ∃ x,neg(A) |
| neg(∃ x,A) | = ∀ x,neg(A) |
|
On montre ensuite par récurrence structurelle sur la formule P que
fnn(P) et neg(P) sont en forme normale
de négation et que de plus fnn(P)≡ P et
neg(P)≡ ¬ P.
Dans le membre droit de chaque équation, il y a le même nombre de connecteurs logiques ∧,∨,∀,∃ que dans le membre gauche. Le symbole d’implication est remplacé par le symbole ∨. On ajoute un symbole de négation uniquement dans le cas de la fonction neg appliquée à une instance de prédicat. Dans le cas de la formule a0⇒ a1⇒…⇒ an) qui a n connecteurs logiques, la forme normale de négation
¬ a0∨¬ a1 …∨ an en a 2n.
Cela correspond au pire cas. On peut montrer que si P est une formule avec n connecteurs, alors
fnn(P) a au plus 2n connecteurs et neg(P) au plus 2n+1 connecteurs .
D’autre part, les littéraux pourront très souvent se traiter “directement” comme les formules atomiques sans introduire plus de complexité.
□
Exemple 1 Soient p et q des variables propositionnelles et
soit la formule ((p ⇒ q) ⇒ p) ⇒ p que l’on veut mettre en forme normale de négation.
On élimine d’abord les implications, cette formule devient : ¬ (¬ (¬ p ∨ q) ∨ p) ∨ p .On peut ensuite repousser les négations en commençant par l’extérieur. On obtient la formule :
((¬ p ∨ q) ∧ ¬ p)) ∨ p.
Cette formule est en forme normale de négation. On pourra remarquer que sur le plan sémantique, cette formule peut encore se simplifier en ¬ p ∨ p en utilisant le fait que (a ∨ b)∧ a≡ a puis en ⊤.
Ci-dessous les représentations sous forme d’arbre, de la formule initiale, puis après élimination des implications et enfin sous forme normale de négation :
3.1.2 Clauses
Définition 2 (Clause)
On appelle clause une formule qui n’utilise
que des littéraux et la disjonction.
 Un litteral tout seul est une clause dans laquelle il n’y a pas de disjonction. En particulier ⊤ et ⊥ sont des clauses. Si on veut faire apparaître une disjonction, on peut toujours rééecrire le littéral l en l∨ ⊥.
Un litteral tout seul est une clause dans laquelle il n’y a pas de disjonction. En particulier ⊤ et ⊥ sont des clauses. Si on veut faire apparaître une disjonction, on peut toujours rééecrire le littéral l en l∨ ⊥.
Exemple 2
Soi p,q des variables propositionnelles.
-
⊥, p,⊤,¬ p,p∨ q,p∨ q∨¬ p sont des
clauses.
- p∧ q,p∧ ⊤, p⇒ q ne sont pas des
clauses.
Etre une clause est une propriété syntaxique des formules. Une formule peut être équivalente à une clause sans être une clause elle-même.
Clause sous forme simplifiée
Les clauses peuvent se simplifier.
La disjonction est associative et commutative on peut donc réarranger les littéraux librement à l’intérieur de la formule sans en changer le sens et en restant syntaxiquement une clause.
On a également P∨ P≡ P, P∨ ¬ P≡ ⊤, P∨ ⊤ ≡ ⊤, P∨ ⊥ ≡ P.
Une clause peut donc soit être de la forme ⊥ ou ⊤, soit s’écrire l1∨ l2∨… ∨ ln avec li un littéral autre que ⊥ ou ⊤. On peut représenter une clause comme un ensemble de litteraux tous distincts. La clause qui correspond à la formule atomique ⊥ est appelée clause vide elle correspond par convention à un ensemble vide de littéraux. Si une clause contient une instance de prédicat et sa négation alors elle est de la forme p∨¬ p∨ Q et se simplifie en ⊤. On appelle clause triviale, une clause qui soit contient le littéral ⊤, soit contient une instance de prédicat p et sa négation ¬ p.
On peut toujours réécrire une clause de manière à ce que
chaque instance de prédicat R(t1,…,tn) apparaisse au plus une fois sous forme
positive (littéral R(t1,…,tn)) ou négative (littéral ¬ R(t1,…,tn)).
Proposition 2
Une clause est équivalente à ⊤ ou ⊥ ou bien à une disjonction
d’instances de prédicats (sous forme positive ou négative) dans laquelle chaque
instance apparaît au plus une fois.
Preuve:
Si une instance de prédicat p apparaît deux fois sous
forme positive ou deux fois sous forme négative, alors en utilisant
q∨ q≡ q on peut retirer une des occurrences sans
changer la valeur de la formule.
Si une instance de prédicat p
apparaît une fois sous forme positive et une fois sous forme
négative alors, en utilisant p∨ ¬ p ≡ ⊤, on
peut remplacer ces deux occurrences par la formule
⊤.
Une clause qui contient ⊤ est simplement équivalente à ⊤
Si une clause est de la forme P∨⊥ on peut la simplifier en la clause P.
□
Une clause est donc caractérisée par un ensemble d’instances de prédicats, chacun associé à un signe pour
indiquer s’il apparait en position positive ou négative. On peut représenter une clause non triviale par un ensemble d’instances de prédicat associés à des booléens (true si l’instance apparait positivement et false si elle apparait négativement).
Par exemple la clause p∨¬ q peut se représenter par l’ensemble {(p,true);(q,false)}.
Par convention, la clause associée à un ensemble
vide de littéraux est interprétée comme la formule fausse
⊥. En effet une disjonction de formules est vraie lorsque l’une des formules qui forme la disjonction est vraie. S’il n’y a pas de formule, alors la propriété est fausse.
Exercice 1
Donner les équations récursives d’une fonction clauseset
qui étant donné un ensemble d’instances de prédicats, chacun associé à un booléen représentant son signe, construit la formule correspondante sous forme de clause.
Si L={l1,…,ln} est un ensemble fini de littéraux, on notera L la formule logique correspondant à la clause l1∨ …∨ ln.
Proposition 3
Soient L1 et L2 des ensembles de littéraux, si
L1⊆ L2 alors L_1⊨ L_2
Preuve:
si L1⊆ L2 alors
soit L3 = L2 ∖ L1. On a L2=L1∪ L3 et L_2≡ L_1∨ L_3. Or A⊨ A∨ B, d’où L_1⊨ L_2.
□
La réciproque est vraie à condition de la clause correspondant à L2 ne soit pas triviale.
Proposition 4
Soient L1 et L2 des ensembles de littéraux clos, si
L_1⊨ L_2 et L2 n’est pas une clause triviale alors L1⊆ L2
Preuve:
si L_1⊨ L_2 et L1⊈L2, alors il existe un littéral l∈ L1 tel que l∉L2.
Comme L2 porte sur des instances de prédicat clos différentes (sinon elle serait triviale), on peut choisir une interprétation J telle que J⊭L_2. Il suffit de choisir l’interprétation J pour que tous les littéraux de L2 soient faux.
L’instance de prédicat du littéral l∈ L1 pourrait apparaître dans L2 mais avec un signe opposé (équivalent à ¬ l).
On a que J⊭¬ l par construction de J donc J⊨ l.
Dans le cas où l’instance de prédicat sous-jacente à l n’apparait pas dans L2 on peut étendre J pour que le littéral l soit vrai.
Comme l∈ L1, et que J⊨ l, on a que J⊨ L_1 et donc une contradiction avec le fait que L_1⊨ L_2 et que J⊭L2.
□
En particulier deux clauses non triviales sont logiquement équivalentes si et seulement si elles correspondent aux mêmes ensembles de littéraux.
Par contre il existe des formules logiques qui ne sont pas équivalentes à des clauses.
En effet si on se donne n variables propositionnelles différentes, on peut construire 3n clauses différentes non équivalentes (pour chaque variable, on choisit si elle apparaît ou non dans la clause, et lorsqu’elle apparaît avec quel signe). Si on ajoute la clause triviale, on a donc 3n+1 clauses qui ne sont pas logiquement équivalentes.
Or le nombre de formules non logiquement équivalentes avec n variables propositionnelles est 22n (nombre de tables de vérité différentes portant sur les 2n interprétations).
Pour n=0 et n=1 ces deux nombres coincident, mais pour n=2 on a seulement 10 clauses etpar contre 16 formules non logiquement équivalentes. Il y a donc certaines “vérités” que l’on ne peut pas représenter par une clause. On va voir dans la suite que par contre chaque formule peut être rendue équivalente à la conjonction d’un ensemble fini de clauses.
3.1.3 Formes normales conjonctives et disjonctives
Dans la suite, on ne s’intéresse qu’à la partie propositionnelle du langage c’est-à-dire à des formules qui ne contiennent pas de quantificateur.
Définition 3 (Forme normale conjonctive, forme clausale)
Une formule est dite en forme normale conjonctive (abrégé en FNC, CNF en anglais) si elle
s’écrit comme une conjonction de clauses.
On peut représenter une formule en forme normale conjonctive par un ensemble de clauses, on parle alors de forme clausale.
Par convention, une
conjonction d’un ensemble vide de formules est définie comme la
formule vraie ⊤.
En effet, la conjonction de formules est vraie lorsque toutes les formules qui forment la conjonction sont vraies. S’il n’y a pas de formule, alors la propriété est vraie.
Reconnaître une formule en forme normale conjonctive
On caractérise les formules en forme normale conjonctive en disant que cette formule est une conjonction de disjonction de littéraux. Mais il faut faire attention qu’il y a des cas de limites :
-
Conjonction d’un ensemble vide de formules : toujours vrai ⊤
- Disjonction d’un ensemble vide de formules : toujours faux ⊥
- Conjonction d’un ensemble réduit à une formule {A} : la formule elle-même A
- Disjonction d’un ensemble réduit à une formule {A} : la formule elle-même A
Une formule en forme normale disjonctive peut très bien ne comporter aucun symbole ∨ ni symbole ∧. Une disjonction de littéraux est en forme normale conjonctive, de même pour une conjonction de littéraux. Pour qu’une formule soit en forme normale conjonctive, il faut et il suffit qu’elle ne comporte que les connecteurs logiques ∨, ∧ et des littéraux, et de plus que dans la représentation sous forme d’arbre, il n’y ait pas de connecteur ∧ en dessous d’un connecteur ∨.
Exemple 3 (Forme normale conjonctive)
-
Les formules ⊥, ⊤, p∨¬
q, p∧¬ q, (p∨ q)∧¬ q sont en
forme normale conjonctive.
- Les formules p⇒ q,
¬ (p∧ q), (p∧ q)∨ q, (p∧ (q ∨ r))∨ q ne sont
pas en forme normale conjonctive.
Mise en forme normale conjonctive
Proposition 5 Toute formule P propositionnelle admet une forme normale conjonctive, c’est-à-dire qu’il existe une formule Q équivalente à P et qui est en forme normale conjonctive.
Pour démontrer ce résultat, nous allons utiliser une autre propriété
qui dit que toute fonction booléenne f à n arguments
peut être associée à une formule Q en forme normale conjonctive, telle que la table de vérité de Q correspondra à la fonction f.
On commence par définir plus précisément la notion de fonction booléenne associée à une formule propositionnelle. Cette notion suppose que les variables propositionnelles de la formule sont ordonnées.
Définition 4 (Fonction booléenne associée à une formule,[P]B)
Soit P une formule du calcul propositionnel qui contient n variables propositionnelles nommées p1,…,pn. La fonction booléenne associée à P est une fonction de Bn→B notée [P]B.Elle est définie par [P]B(b1,…,bn)=val(I{b1,…,bn},P) avec I{b1,…,bn} l’interprétation dans laquelle chaque variable pi a la valeur bi.
La fonction [P]B correspond à la table de vérité de la formule P, dans laquelle les variables sont ordonnées suivant les colonnes et chaque ligne correspond à une entrée de la fonction.
Exemple 4
Soit la formule P =def p1∨ p2⇒ p3. La table de vérité et la fonction associée sont donnés ci-dessous| p1 | p2 | p3 | P |
| _ | _ | V | V |
| V | _ | F | F |
| F | V | F | F |
| F | F | F | V |
| |
|
| | [P]B(V,V,V) | =V |
| [P]B(V,V,F) | =F |
| [P]B(V,F,V) | =V |
| [P]B(V,F,F) | =F |
| [P]B(F,V,V) | =V |
| [P]B(F,V,F) | =F |
| [P]B(F,F,V) | =V |
| [P]B(F,F,F) | =V |
| |
|
Proposition 6 Pour toute fonction booléenne f à n arguments, on peut trouver une formule Q en forme normale conjonctive telle que f=[Q]B.
Preuve:
On s’intéresse à l’ensemble Z des n-uplets pour lesquels la fonction f est fausse, c’est-à-dire
| Z | | {(b1,…,bn) | f(b1,…,bn)=F} |
Dans la table de vérité, il suffit de s’intéresser aux lignes où la valeur de la formule est F.
L’ensemble Z est fini. Si cet ensemble est vide alors f=[⊤]B qui est en forme normale conjonctive. On cherche une formule propositionnelle Q qui dépend des variables p1,…,pn correspondant à f. La variable propositionnelle pi correspond à la propriété “le i-ème argument de f est vrai”. La propriété Q doit être vraie lorsque la fonction est vraie et donc doit exprimer que les arguments ne sont pas dans Z. Pour un élément (b1,…,bn), la formule qui dit que les arguments ne correspondent pas à cette valeur est
l1 ∨ l2 ∨ … ∨ ln avec li=pi si bi=F et li=¬ pi si bi=V. Cette formule est une clause.
Il suffit ensuite de prendre la conjonction des clauses pour chaque élément de Z.
□
Exemple 5
Soit la formule P =def (p1 ⇒ p2) ⇒ (¬ p1 ∧ p2), on commence par écrire la table de vérité :
|
| | p1 | p2 | p1 ⇒ p2 | ¬ p1 ∧ p2 | (p1 ⇒ p2) ⇒ (¬ p1 ∧ p2) |
| V | V | V | F | F |
| V | F | F | F | V |
| F | V | V | V | V |
| F | F | V | F | F |
|
Les lignes qui nous intéressent sont la première et la dernière et on doit trouver une formule qui dit exactement que l’on n’est pas dans un de ces deux cas.
La formule qui dit que l’on n’est pas dans le cas de la ligne 1 est ¬ p1 ∨ ¬ p2 et la formule qui dit que l’on n’est pas dans le cas de la ligne 4 est p1 ∨ p2.
La forme normale conjonctive est donc (¬ p1 ∨ ¬ p2) ∧ (p1 ∨ p2).
Si on parle d’une formule P quelconque, on peut lui associer une fonction booléenne [P]B. Cette fonction booléenne peut, d’après le résultat précédent, se représenter par une formule Q en forme normale conjonctive. On a donc [P]B=[Q]B. Ces deux formules ont même table de vérité par construction et donc sont équivalentes.
Mise en forme normale conjonctive syntaxique
Construire la table de vérité d’une formule est trop complexe en général et donc on va plutôt utiliser des méthodes syntaxiques. La formule (a ∧ b) ∨ c n’est pas en forme normale conjonctive car il y a une disjonction qui porte sur une formule qui n’est pas un littéral. La règle de distributivité permet d’inverser les conjonctions et les disjonctions.
| (a ∧ b) ∨ c | ≡ (a ∨ c) ∧ (b ∨ c) |
| (a1 ∧ … ∧ an) ∨ (b1 ∧ … ∧ bp) | ≡
(a1∨ b1)∧…∧ (a1∨ bp)
|
| | ∧…∧ (an∨ b1)∧…∧ (an∨ bp)
|
| | |
| (a1 ∧ b1) ∨ (a2 ∧ b2) ∨ (a3 ∧ b3) | ≡
(a1∨ a2∨ a3)∧ (a1∨ a2∨ b3) |
| | ∧ (a1∨ b2∨ a3)∧ (a1∨ b2∨ b3) |
| | ∧ (b1∨ a2∨ a3)∧ (b1∨ a2∨ b3) |
| | ∧ (b1∨ b2∨ a3) ∧ (b1∨ b2∨ b3) |
| (a1 ∧ b1) ∨ … ∨ (an ∧ bn) | |
|
On en déduit un algorithme de mise en forme normale conjonctive.
Pour cela, on construit une fonction fnc(P) qui calcule un ensemble de clauses équivalent à P
et on utilise de manière auxiliaire une fonction fnc-neg(P) qui construit un ensemble de clauses équivalent à ¬ P. On aura besoin d’une autre fonction auxiliaire sh, qui prend en argument deux ensembles de clauses E et E′ et qui construit un nouvel ensemble de clauses avec toutes les combinaisons possibles C∨ C′ avec C∈ E et C′∈ E′, c’est-à-dire que sh(E,E′)={C∨ C′|C∈ E, C′∈ E′}. Si E contient n clauses et si E′ contient p clauses alors sh(E,E′) peut contenir jusqu’à n× p clauses (il pourrait y en avoir moins si certaines clauses se simplifient). Pour faire cette opération de manière efficace, il sera utile de rerésenter les clauses comme des ensembles de littéraux, mais dans la suite on considère les clauses comme des formules ordinaires.
|
| | fnc(⊥) | = {⊥} |
| fnc(⊤) | =∅ |
| fnc(x) | ={x} |
| fnc(¬ P) | =fnc-neg(P) |
| fnc(P∧ Q) | =fnc(P)⋃ fnc(Q) |
| fnc(P∨ Q) | =sh(fnc(P),fnc(Q)) |
| fnc(P⇒ Q) | =sh(fnc-neg(P),fnc(Q)) |
|
| | fnc-neg(⊥) | =∅ |
| fnc-neg(⊤) | = {⊥} |
| fnc-neg(x) | ={¬ x} x instance de prédicat |
| fnc-neg(¬ P) | =fnc(P) |
| fnc-neg(P∨ Q) | =fnc-neg(P)⋃ fnc-neg(Q) |
| fnc-neg(P∧ Q) | =sh(fnc-neg(P),fnc-neg(Q)) |
| fnc-neg(P⇒ Q) | =fnc(P)⋃ fnc-neg(Q) |
|
On a recours à deux fonctions pour calculer la forme normale conjonctive car on part d’une formule quelconque qui n’est pas déjà en forme normale de négation.
Exercice 2
Donner les équations récursives pour définir une fonction fnn2fnc qui étant donnée une formule en forme normale de négation, calcule l’ensemble des clauses correspondant à sa forme clausale.
Forme normale disjonctive
On définit de manière duale la notion de forme normale disjonctive.
Définition 5 (Forme normale disjonctive)
-
Une conjonction élémentaire est une formule uniquement composée de littéraux et de conjonctions.
- Une formule P est en forme normale disjonctive (abrégé en FND, DNF en anglais), si elle s’écrit comme une disjonction de conjonctions élémentaires.
Comme dans le cas des clauses, les conjonctions élémentaires peuvent se simplifier de manière à ne garder que celles dans lesquelles une variable propositionnelle apparaît une seule fois, en effet si p et ¬ p apparaissent dans la même conjonction alors celle-ci est équivalente à ⊥. Comme ⊥∨ Q≡ Q, on peut simplement supprimer la conjonction.
Exemple 6 (Forme normale disjonctive)
-
Les formules ⊥, ⊤, p∨¬
q, p∧¬ q, (p∧ q)∨ q sont en
forme normale disjonctive.
- Les formules p⇒ q,
¬ (p∨ q), (p∨ q)∧¬ q, (p∧ (q ∨ r))∨ q ne sont
pas en forme normale disjonctive.
Proposition 7
Pour toute formule propositionnelle P, il existe une formule Q équivalente en forme normale disjonctive.
Preuve: On remarque que si P est en forme normale conjonctive, alors la forme normale de négation de ¬ P est en forme normale disjonctive.
Il suffit donc de prendre la forme normale de négation de la négation de la forme normale conjonctive de la formule ¬ P pour obtenir une formule en forme normale disjonctive équivalent à P.
□
Forme Normale Disjonctive à partir de la table de vérité
Comme précédemment, on peut aussi construire directement la FND à partir de la table de vérité de la formule P. On suppose que les variables propositionnelles sont {p1,…,pn}.
On s’intéresse à l’ensemble O des n-uplets (b1,…,bn), pour lesquels la table de vérité donne la valeur vrai.
Pour chaque ligne on construit une conjonction élémentaire
l1 ∧ l2 ∧ … ∧ ln avec li=pi si bi=V et li=¬ pi si bi=F. Il suffit ensuite de prendre la disjonction de ces formules pour trouver une formule équivalente à P.
Exemple 7
En reprenant la formule P de l’exemple 5, on
obtient la forme normale disjonctive :
Si une formule est en forme normale disjonctive alors il est facile d’en
trouver un modèle. On suppose que les branches de la disjonction
sont en forme “simplifiée” c’est-à-dire qu’une variable
propositionnelle apparaît dans un seul littéral. Il suffit de choisir
une des branches de la disjonction. Pour chaque variable
propositionnelle x qui apparaît dans un littéral l on
prend dans le modèle x↦ V si l=x et
x↦ F si l=¬ x. Il peut arriver qu’il n’y ait
aucune composante en forme simplifiée: c’est le cas lorsque la formule
initiale est équivalente à ⊥. Dans ce cas, il n’y a pas de
modèle, la formule est insatisfiable.
Efficacité
Cependant, la mise en forme normale n’est pas forcément la meilleure
manière de trouver un modèle. En effet, cette forme normale peut être
exponentiellement plus grosse que la formule initiale. C’est le cas par
exemple de la formule (a1∨ b1) ∧…∧ (an ∨
bn) qui a 2n variables et 2n−1 connecteurs. La
forme normale disjonctive s’écrit
∨ci∈{ai,bi}(c1∧… ∧ cn) dans laquelle il y a
2n disjonctions.
Forme normale conjonctive efficace pour la satisfiabilité
Lorsqu’une formule propositionnelle est en forme normale conjonctive, il est facile de voir si elle est valide. En effet si l’ensemble des clauses n’est pas vide, on en choisit une qui est de la forme l1∨… ∨ ln que l’on rend fausse en choisissant une interprétation dans laquelle chacun des li est faux ce qui est possible car ils portent tous sur des variables propositionnelles différentes. Si une des clauses de la forme normale conjonctive est fausse alors il en est de même de la formule.
La forme normale conjonctive de la formule (a1 ∧ b1) ∨ … ∨ (an ∧ bn) s’écrit
∧ci∈{ai,bi}c1∨… ∨ cn qui contient 2n clauses. Cette complexité est intrinsèque car liée à la complexité de décider si une formule propositionnelle est valide.
La forme normale conjonctive est équivalente à la formule initiale. Pour la démonstration automatique, cette équivalence n’est pas forcément nécessaire.
Si on ne s’intéresse qu’à la satisfiabilité, on peut se permettre de
transformer la formule P en une formule Q, telle que P et Q ne sont pas équivalentes, mais seulement equisatisfiables. C’est-à-dire que P est satisfiable si et seulement si Q est satisfiable. Cela nous permet d’introduire de nouvelles
variables propositionnelles dans Q pour éviter l’explosion combinatoire.
Dire que P et Q sont équivalents c’est dire que pour toute interprétation I, on a I⊨ P si et seulement si I⊨ Q alors que dire que P et Q sont equisatisfiables c’est dire qu’il existe une interprétation I telle que I⊨ P si et seulement si il existe une interprétation J telle que J⊨ Q. Deux formules équivalentes sont equisatisfiables mais le contraire n’est pas vrai.
Proposition 8 (Forme clausale equisatisfiable)
Pour toute formule propositionnelle P, il existe un ensemble de clauses clause(P) dont la taille est linéaire par rapport à la taille de P et qui est equisatisfiable, plus précisément pour toute interprétation I :
-
clause(P)⊨ P.
- si I⊨ P alors il existe une interprétation J telle que J⊨ clause(P) qui de plus coincide avec I sur les symboles de P.
La construction se fait de manière récursive sur la structure de la formule que l’on supposera initialement en forme normale de négation.
La formule ne contient donc que des conjonctions, des disjonctions et des littéraux.
Exemple 8
Soit la formule P définie comme
(a1 ∧ b1) ∨ (a2 ∧ ¬ b2) ∨ (¬ a3 ∧
(b3 ∨ c)) ∨ a4 ∨ ¬ b4.
On introduit les variables x1, x2 et x3
pour représenter respectivement (a1 ∧ b1) (x1),
(a2 ∧ ¬ b2) (x2), et (¬ a3 ∧
(b3 ∨ c)) pour (x3).
L’ensemble clause(P) est donc
| {x1 ∨ x2 ∨ x3 ∨ a4 ∨ ¬ b4,
¬ x1 ∨ a1, ¬ x1 ∨ b1, ¬ x2 ∨ a2,
¬ x2 ∨ ¬ b2, ¬ x3 ∨ a3, ¬ x3 ∨ b3 ∨ c
} |
On a dans l’ensemble de clauses obtenus, le même nombre de connecteurs ∨ et ∧ que dans la formule initiale plus un nombre de variables et de clauses égal au nombre de connecteurs ∧ qui se trouvent sous un connecteur ∨ dans la formule initiale (ici 3).
Preuve:
La définition de la fonction clause est bien formée même si elle ne suit pas le schéma récursif structurel usuel. Elle traite tous les cas (pour une formule propositionnelle en forme normale de négation) et les appels récursifs se font sur des formules qui contiennent strictement moins de connecteurs ∧.
Concernant la taille des clauses obtenues, on observe qu’une variable x est introduite chaque fois qu’une expression P∧ Q apparaît sous une disjonction. On crée alors deux sous problèmes ¬ x ∨ P et ¬ x ∨ Q, cette opération fait disparaître une conjonction sous une disjonction sans changer la situation des autres conjonctions.
Montrons maintenant les liens logiques entre l’ensemble des clauses ainsi obtenu et la formule initiale.
Plus précisément, on se donne une interprétation I et on fait le lien entre la vérité de P dans cette interprétation et celle de clause(P). Le cas intéressant est celui dans
lequel on introduit une nouvelle variable propositionnelle. Les autres cas se traitent directement ou par hypothèse de récurrence.
Soit
P =def A ∨ (R ∧ Q), on suppose qu’il n’y a pas de conjonction dans les formules A, R et Q, on se ramène à ce cas en utilisant les hypothèses de récurrence.
On a clause(P) =def {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q} avec x une variable propositionnelle qui n’apparaît pas dans A ∨ (R ∧ Q).
-
Si I⊨ {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q} alors :
-
si I⊨ x, comme I⊨ ¬ x ∨ R on en déduit I⊨ R et de même I⊨ Q, donc I⊨ A ∨ (R ∧ Q)
- si I⊭x, comme I⊨ A∨ x on en déduit I⊨ A, donc I⊨ A ∨ (R ∧ Q)
dans les deux cas on a bien que si I⊨ clause(P) alors I⊨ P donc
clause(P)⊨ P
- Si I⊨ A ∨ (R ∧ Q) alors il faut trouver une interprétation xJ de la variable x pour laquelle on aura
I,xJ⊨ {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q}. On choisit pour xJ la valeur de vérité val(I,Q∧ R) de la formule Q∧ R dans l’interprétation I.
-
si I⊨ Q∧ R alors l’interprétation de x est V et de plus I⊨ Q et I⊨ R. On a donc
I,xJ⊨ {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q}
- si I⊭Q∧ R alors l’interprétation de ¬ x est V et de plus I⊨ A. On a donc
I,xJ⊨ {A ∨ x, ¬ x ∨ R, ¬ x ∨ Q}
on a donc montré qu’une interprétation de P pouvait s’étendre en une interprétation de clause(P).
La formule P est satisfiable exactement lorsque l’ensemble de clauses clause(P) l’est.
□
Exercice 3
-
En utilisant une méthode analogue montrer que pour toute formule propositionnelle P, on peut trouver un ensemble de clauses qui ont au plus trois littéraux tel que cet ensemble est satisfiable si et seulement si la formule P est satisfiable.
3.1.4 Skolémisation
Les transformations précédentes traitent de la partie propositionnelle des formules (sans quantificateur), nous allons dans cette section montrer comment on traite la partie avec quantificateurs.
Forme prénexe
Dans la section 2.3.2 nous avons établi des propriétés d’équivalence qui permettent de ramener les quantificateurs en tête de formule. Si x n’est pas libre dans la formule A alors :
| ∀ x,(A ∧ G(x)) ≡ A ∧ ∀ x,G(x)
∀ x,(A ∨ G(x)) ≡ A ∨ ∀ x,G(x) |
| ∃ x,(A ∧ G(x)) ≡ A ∧ ∃ x,G(x)
∃ x,(A ∨ G(x)) ≡ A ∨ ∃ x,G(x) |
|
 Attention la remontée des quantificateurs au travers d’une négation change le quantificateur (loi de de Morgan) de même lorsqu’il est dans la partie gauche d’une implication. La remontée des quantificateurs se fait après avoir mis la formule en forme normale de négation.
Attention la remontée des quantificateurs au travers d’une négation change le quantificateur (loi de de Morgan) de même lorsqu’il est dans la partie gauche d’une implication. La remontée des quantificateurs se fait après avoir mis la formule en forme normale de négation.
 la remontée naïve des quantificateurs peut engendrer une capture des variables : la condition que x n’est pas libre dans la formule A est essentielle.
la remontée naïve des quantificateurs peut engendrer une capture des variables : la condition que x n’est pas libre dans la formule A est essentielle.
Si x est libre dans A (en plus d’être liée dans ∃ x,G(x)) alors on renomme la variable liée en choisissant une variable z qui n’est pas libre dans A ni dans ∃ x,G(x), on a alors A ∨ ∃ x,G(x) = A ∨ ∃ z,G(z)≡ ∃ z,A ∨ G(z)
Proposition 9 (Forme prénexe)
Toute formule logique P est équivalente à une formule de la forme avec Q l’un des quantificateurs ∀ ou ∃ et A une formule propositionnelle (sans quantificateur). Une formule de la forme Q x1, …, Q xn, A est dite en forme prénexe.
Preuve:
On met la formule P en forme normale de négation, on utilise les équivalences rappelées ci-dessus pour remonter les quantificateurs en renommant si nécessaire les variables liées.
□
 La forme prénexe n’est pas unique. L’ordre des quantificateurs en particulier peut varier en fonction de l’ordre dans lequel on choisit de les faire remonter.
La forme prénexe n’est pas unique. L’ordre des quantificateurs en particulier peut varier en fonction de l’ordre dans lequel on choisit de les faire remonter.
Elimination des quantificateurs existentiels
On a vu qu’intervertir un quantificateur existentiel et un quantificateur universel en général ne préservait pas l’équivalence entre les formules. Nous allons montrer ici que, si on ne s’intéresse qu’à la satisfiabilité, alors on peut se ramener, grace à une transformation appelée la skolemisation, à une formule prénexe qui n’aura que des quantificateurs universels.
La skolemisation est une opération (introduite par le logicien norvégien Thoraf Albert Skolem au 20ème siècle) qui permet de se débarrasser des quantifications existentielles en enrichissant les signatures et en préservant la satisfiabilité des formules.
L’idée de base est que si on s’intéresse à la formule ∀ x,∃ y,P(x,y)
cette formule est vérifiée si pour tout élément d du domaine, on peut trouver un élément e du domaine tel que I,{x↦ d,y↦ e}⊨ P(x,y). En général, la valeur e retenue pour y dépend de la valeur d choisie pour x. On peut exprimer e en fonction de d et donc le problème de trouver un modèle de
∀ x,∃ y,P(x,y) est analogue au problème de trouver un modèle pour ∀ x,P(x,f(x)) dans lequel f est un nouveau symbole de fonction.
De manière plus précise on prouve aisément la propriété de conséquence logique
| ∀ x,P(x,f(x))⊨ ∀ x,∃ y,P(x,y) |
si pour tout x, on a établi que f(x) était dans la relation P avec x, alors a fortiori on sait que pour tout x, il existe un y qui est dans la relation P avec x.
On montre également que si la formule
∀ x,∃ y,P(x,y) est satisfiable alors on peut, à
partir d’un modèle de cette formule, trouver un modèle de la formule
∀ x,P(x,f(x)) en choisissant la “bonne” interprétation
pour la fonction f.
Définition 6 (Elimination d’un quantificateur existentiel)
Soit une formule A dans laquelle apparaît une sous-formule ∃ y,B.
On suppose qu’il y a n variables libres dans ∃ y,B, c’est-à-dire
Vl(∃ y,B)={x1,…,xn}.
On introduit alors dans la signature un nouveau symbole de fonction f à n arguments (si n=0 alors f est juste une constante).
On introduit la formule A′ qui est la formule A dans laquelle on a remplacé la sous-formule ∃ y,B par
B[y← f(x1,…,xn)].Pour que cette opération soit licite il suffit que les variables x1,…,xn ne soient pas liées dans B ce qui peut toujours être garanti quite à effectuer des renommages de variables liées dans B.
Exemple 9 On suppose que l’on a un symbole de prédicat binaire P. On élimine le quantificateur existentiel dans les formules suivantes :
-
∀ x,∃ y,P(x,y) : la sous-formule existentielle à traiter est
∃ y,P(x,y). Elle a une seule variable libre x. On introduit donc un nouveau symbole de fonction f avec un seul argument et on élimine le quantificateur existentiel en remplaçant y par f(x). La formule devient ∀ x,P(x,f(x))
- ∀ x y,∃ z,P(x,z)∧ P(z,y) : la sous-formule existentielle à traiter est
∃ z,P(x,z)∧ P(z,y). Elle a deux variables libres x,y. On introduit donc un nouveau symbole de fonction g avec deux argument et on élimine le quantificateur existentiel en remplaçant z par g(x,y).
La formule devient ∀ x y,P(x,g(x,y))∧ P(g(x,y),y)
- ∃ x,∀ y,P(x,y) : la sous-formule existentielle à traiter est la formule elle même. Elle n’a pas de variable libre. On introduit donc un nouveau symbole de constante a et on élimine le quantificateur existentiel en remplaçant x par a. La formule devient ∀ y,P(a,y)
 Dans beaucoup d’ouvrages, l’élimination du quantificateur existentiel se fait après avoir mis la formule en forme prénexe. On choisit alors l’arité du symbole de fonction introduit en fonction du nombre de quantifications universelles préalables. L’idée étant que si on a une alternance ∀ x,∃ y alors le choix de y peut dépendre de x.
Dans beaucoup d’ouvrages, l’élimination du quantificateur existentiel se fait après avoir mis la formule en forme prénexe. On choisit alors l’arité du symbole de fonction introduit en fonction du nombre de quantifications universelles préalables. L’idée étant que si on a une alternance ∀ x,∃ y alors le choix de y peut dépendre de x.
Dans l’approche présentée ici, on s’intéresse à la sous-formule ∃ y,A et aux dépendances de la condition que doit vérifier y. Si A ne dépend pas de x alors dès qu’on a une valeur pour y qui vérifie A, cette valeur fonctionnera pour toute valeur de x, il n’est donc pas utile de faire dépendre y de la valeur de x.
La méthode prénexe est bien sûr correcte mais peut amener à des dépendances artificielles. Ainsi si on part d’une formule (∀ x, P(x))∨ ∃ y,¬ P(y), la formule ∃ y,¬ P(y) étant close, le symbole introduit pour remplacer l’existentielle est une constante a et on obtient la formule (∀ x, P(x))∨ ¬ P(a). Le domaine de Herbrand associé est constitué de la seule constante a. Une des formes prénexe est (∀ x, ∃ y, P(x)∨ ¬ P(y) et, par la méthode prénexe, il faut introduire un symbole de fonction unaire f et la formule devient (∀ x, P(x)∨ ¬ P(f(x)), le domaine de Herbrand associé est alors infini.
Avoir un domaine de Herbrand plus restreint simplifie la recherche de modèle.
Proposition 10 Soit A une formule en forme normale de négation.
Soit A′ obtenue à partir de A en éliminant un quantificateur existentiel suivant la procédure précédente. On a alors
A′⊨ A et tout modèle de A peut être transformé en un modèle de A′ qui coincide avec celui de A sauf pour l’interprétation du nouveau symbole f.
Preuve:
La première propriété est une conséquence de B[y← f(x1,…,xn)]⊨ ∃ y,B et du fait que A est en forme normale de négation. En effet on vérifie aisément les propriété de stabilité de la conséquence logique (en l’absence de négation) : si Q⊨ R alors pour n’importe quelle formule P on a
| Q∧ P⊨ R∧ P Q∨ P⊨ R∨ P ∀ x,Q⊨ ∀ x, R ∃ x,Q⊨ ∃ x, R |
Pour la seconde propriété on suppose construit un modèle I de la formule A.
La formule B a comme variables libres les variables x1… xn, y. On regarde dans le modèle l’ensemble des n+1-uplets (d1,…,dn,e) tels que I,{x1↦ d1,…,xn↦ dn,y↦ e}⊨ B.
On peut à partir de cette relation construire une fonction fJ ∈ Dn→ D telle que I,{x1↦ d1,…,xn↦ dn,y↦ fJ(d1,…,dn)}⊨ B s’il existe e tel que I,{x1↦ d1,…,xn↦ dn,y↦ e}⊨ B et fJ(d1,…,dn)=d avec d une valeur arbitraire de D si pour tout e, I,{x1↦ d1,…,xn↦ dn,y↦ e}⊭B.
On peut alors construire une interprétation J sur le même domaine D que I, qui étend l’interprétation I avec l’interprétation du symbole de fonction f comme la fonction fJ.
Cette interprétation rend vraie la formule (∃ y,B) ⇔ B[y← f(x1,…,xn)] pour tout environnement {x1↦ d1,…,xn↦ dn}. Elle rend donc aussi vraie la formule ∀ x1… xn,((∃ y,B) ⇔ B[y← f(x1,…,xn)]).
Par ailleurs cette interprétation rend vraie la formule A car J est une extension de I qui est un modèle de A.
Comme par ailleurs on peut montrer
∀ x1 … xn,((∃ y,B) ⇔ B[y← f(x1,…,xn)]) ⊨ A⇔ A′
car A′ est obtenue à partir de A en remplaçant ∃ y,B par B[y← f(x1,…,xn)],
on en déduit que J est un modèle de A′.
□
On peut itérer l’opération précédente pour éliminer tous les quantificateurs existentiels d’une formule. Chaque élimination de quantificateur introduit un nouveau symbole de fonction.
Si on applique ces transformations à une formule A en forme normale de négation, on obtient une formule B sans quantificateur existentiel telle que
-
B ⊨ A
- Tout modèle de A peut être étendu sur les symboles de B qui ne sont pas dans A en un modèle de B.
Proposition 11
Soit A une formule en forme normale de négation et B une formule obtenue par élimination des quantificateurs existentiels de A.
-
Si B est valide alors A l’est aussi.
- Si B est satisfiable alors A l’est aussi.
- Si B est insatisfiable alors A l’est aussi.
Preuve:
Les deux premières propriétés sont des conséquences directes de B⊨ A alors que la dernière vient du fait que s’il existait un modèle de A alors il y en aurait aussi un de B.
□
Exemple 10
Soit la formule (∃ x,P(x)) ∧ (∃ z,¬ P(z)). La skolemisation (utilisée deux fois) introduit deux nouvelles constantes a et b et donne la formule
P(a) ∧ ¬ P(b).
Cette formule est satisfiable, par contre si on avait utilisé deux fois la même constante a on aboutirait à la formule P(a) ∧ ¬ P(a) qui est insatisfiable.
Proposition 12 (Skolemisation, Forme de Skolem)
Soit A une formule close alors il existe une formule B en forme normale de négation et sans quantificateur telle que si Vl(B)={x1,…,xn} on a
-
(∀ x1 … xn, B) ⊨ A
- si A a un modèle alors il en est de même de ∀ x1… xn, B
L’opération de transformation s’appelle la slolémisation. On dit que la formule ∀ x1 … xn, B est la forme de Skolem de A ou encore la formule skolémisée associée à A.Preuve:
Il suffit d’éliminer les symboles d’implication et mettre la formule en forme normale négative. On applique ensuite l’élimination des quantificateurs existentiels suivant la procédure vue précédemment. On fait ensuite remonter les quantificateurs universels (en s’assurant au préalable qu’il n’y en n’a pas deux différents qui portent sur une variable de même nom) et en utilisant les équivalences
A ∘ ∀ x, B ≡ ∀ x, (A ∘ B) lorsque x n’est pas libre dans B et ∘ ∈ {∨,∧}.
Une fois que tous les quantificateurs universels sont en tête (c’est-à-dire que la formule est en forme prénexe) il suffit de les éliminer pour obtenir la formule B.
□
Cette opération peut nous permettre de montrer la validité d’une formule. En effet la validité d’une formule A est équivalent à l’insatisfiabilité de la formule ¬ A qui se ramène donc à l’insatisfiabilité de la forme skolémisée de ¬ A. Comme la forme skolémisée est une formule universelle, le théorème de Herbrand nous permet de ramener la satisfiabilité à l’existence d’un modèle construit sur le domaine de Herbrand.
Exemple 11
Soit la formule A =def (∀ x, (P(x) ⇒ Q(x))) ⇒ (∀ x, P(x)) ⇒ ∀ x, Q(x). Pour montrer que A est valide, on montre que ¬ A est insatisfiable. Pour cela, on skolemise ¬A en passant par les étapes suivantes :
-
Forme normale négative de ¬ A : (∀ x, (¬ P(x) ∨ Q(x))) ∧ (∀ y, P(y)) ∧ ∃ z,¬ Q(z)
- Elimination du quantificateur existentiel : (∀ x, (¬ P(x) ∨ Q(x))) ∧ (∀ y, P(y)) ∧ ¬ Q(a)
- Mise en forme prénexe : ∀ x y, ((¬ P(x) ∨ Q(x))∧ P(y) ∧ ¬ Q(a))
- Domaine de Herbrand : D={a}
- Instances closes : {(¬ P(a) ∨ Q(a)) ∧ P(a) ∧ ¬ Q(a)} insatisfiable
D’après le théorème de Herbrand, la formule
∀ x y, ((¬ P(x) ∨ Q(x))∧ P(y) ∧ ¬ Q(a)) est insatisfiable et donc il en est de même de la formule ¬ A donc A est valide.
Définition 7 (Fermeture universelle)
Soit P une formule dont les variables libres sont { x1,…, xn}. On appelle fermeture universelle de la formule P et on notera ∀(P) la formule ∀ x1,…, xn,P. Cette formule est close (sans variable libre). L’opération de permutation de deux quantificateurs universels ne change pas le sens de la formule donc l’ordre dans lequel les variables apparaissent dans les quantificateurs n’a pas d’importance.
Skolemisation d’un ensemble de formules.
Si on se donne un ensemble de formules A1,…,An on peut traiter la skolémisation de manière indépendante pour chaque formule (en introduisant évidemment des symboles différents). On obtient pour chaque Ai une formule Bi sans quantificateurs telle que ∀(Bi)⊨ Ai.
On en déduit aisément que :
-
∀(B1),…,∀(Bn)⊨ A1∧…∧ An
- S’il existe un modèle des formules A1,…,An alors on a aussi un modèle des formules
∀(B1),…,∀(Bn).
Forme clausale d’une formule avec quantificateur
Définition 8 (Forme clausale d’une formule avec quantificateur)
La forme clausale d’une formule P est un ensemble de clauses C={C1,…,Cp}. Cet ensemble de clauses s’obtient en construisant la forme de skolem de la formule P qui s’écrit ∀ x1 … xn, A avec A formule propositionnelle. L’ensemble de clauses C={C1,…,Cp} est ensuite obtenu en mettant en forme normale conjonctive la formule A. On a alors
-
C1,…,Cp ⊨ A
- ∀(C1),…,∀(Cp)⊨ P
- S’il existe un modèle de P alors on peut l’étendre en un modèle des formules
∀(C1),…,∀(Cp).
Exercice 4
On part de la formule A =def (∃ x, ∀ y, R(x,y)) ⇒ (∀ y, ∃ x, R(x,y)).-
Donner la forme normale de négation de la formule ¬ A
- Donner la forme de skolem de la formule ¬ A
- Donner la forme clausale de ¬ A
- la formule ¬ A est-elle satisfiable ? La formule A est-elle valide ?
3.2 Représentations alternatives des formules
Dans cette section, nous explorons quelques voies alternatives aux connecteurs usuels pour représenter les formules de la logique. Nous détaillerons sous forme principalement d’exercice la représentation à l’aide de diagrammes binaires de décision.
3.2.1 Restrictions sur les connecteurs
On a vu au travers des équivalences que de nombreuses formules différentes syntaxiquement pouvaient représenter la même vérité. Une question naturelle qui se pose est alors de savoir si on peut se passer complètement de certains connecteurs logiques et quantificateurs, sans perdre en expressivité.
Les lois de de Morgan nous permettent, à l’aide de la négation, de supprimer les implications, l’un des deux quantificateurs ∀ ou ∃ et l’un des connecteurs ∨ ou ∧.
On peut éliminer la négation en utilisant l’équivalence ¬ A≡ A ⇒⊥ et représenter n’importe quelle formule logique en utilisant uniquement les connecteurs logiques ⊥, ⇒ et un quantificateur au choix. Par exemple la conjonction de deux formules A et B peut se représenter par la formule (A⇒ B⇒ ⊥)⇒⊥ dont on vérifie qu’elle ne peut être vraie que si A⇒ B⇒ ⊥ est faux et donc que A et B sont vrais.
On peut éliminer ⊥ en le remplaçant par a∧¬ a avec a une variable propositionnelle. De même ⊤ peut être remplacé par a∨¬ a ou a⇒ a.
Par contre on ne peut pas se débarrasser simultanément de la négation et de l’implication. En effet, si une formule P n’utilise que les connecteurs ∨ et ∧, alors la fonction booléenne correspondant [P]B est croissante (en considérant l’ordre F<V). Donc on ne peut représenter avec juste ∨ et ∧ des fonctions booléennes comme la négation qui ne sont pas croissantes.
La mise en forme normale conjonctive montre que l’on peut représenter toutes les formules avec les deux quantificateurs, les connecteurs ∨ et ∧ (dont on peut même restreindre l’imbrication) et des négations limitées aux littéraux.
 La skolémisation élimine les quantifications existentielles mais la formule obtenue n’est pas équivalente à la formule initiale, elle peut être fausse dans des interprétations qui rendent vraies la formule initiale.
La skolémisation élimine les quantifications existentielles mais la formule obtenue n’est pas équivalente à la formule initiale, elle peut être fausse dans des interprétations qui rendent vraies la formule initiale.
3.2.2 Connecteurs alternatifs
Il est possible d’introduire d’autres connecteurs propositionnels binaires qui vont nous donner des représentations différentes des formules.
Le plus connu est le ou exclusif noté ⊕ qui est défini pour satisfaire les équivalences
| x⊕ y ≡ x∨ y ∧ ¬ (x∧ y) ≡ (x∧ ¬ y) ∨ (¬ x ∧ y) ≡ ¬ (x⇔ y) |
.
On peut coder toutes les fonctions booléennes à l’aide des seuls connecteurs ⊕,∧,⊤.
Les opérations ⊕ et ∧ munissent l’ensemble des booléens d’une structure d’anneau de Boole.
L’opération ⊕ est utile comme opérateur simple de cryptographie bit-à-bit d’un message. On utilise le fait que x⊕ x=⊥ et x⊕ ⊥ =x, ainsi que l’associativité de ⊕. Si on dispose d’une clé secrète key, le message m crypté sera m⊕ key, il pourra être décrypté en lui appliquant la même opération (m⊕ key)⊕ key
Il est même possible de représenter toutes les fonctions booléennes à l’aide uniquement de variables propositionnelles et d’un unique connecteur binaire : la barre de Sheffer x∣ y également appelée opérateur NAND et qui est défini comme la négation de la conjonction x∣ y≡ ¬(x∧ y), on vérifie aisément que x∣ x≡ ¬ x, x∣ ¬ x≡ ⊤, (x∣ y)∣(x∣ y)≡ ¬ (x∣ y) ≡ x∧ y et ces constructions sont suffisantes pour reconstruire toutes les formules propositionnelles.
3.2.3 Diagrammes de décision binaire
Une représentation alternative de la partie propositionnelle des formules est l’utilisation d’un connecteur de conditionnelle à trois arguments.
IF(P,Q,R). C’est d’une part une construction naturelle dans les langages de programmation, mais surtout, en limitant les conditionnelles à porter sur des variables propositionnelles, cette représentation des formules propositionnelles devient très efficace. Elle est largement utilisée en démonstration automatique.
IF-expressions.
On introduit un connecteur logique IF(P,Q,R) qui a la même table de vérité que la formule (P∧ Q) ∨ (¬ P ∧ R), ou de manière équivalente à (P⇒ Q) ∧ (¬ P ⇒ R).
On représente n’importe quelle fonction booléenne en utilisant ce connecteur ainsi que les formules ⊥ et ⊤.
Pour s’en convaincre il suffit de remarquer que :
| IF(P,⊥,⊤) | ≡ ¬ P |
| IF(P,Q,⊥) | ≡ P ∧ Q |
| IF(P,⊤,Q) | ≡ P ∨ Q |
| IF(P,Q,⊤) | ≡ P ⇒ Q
|
|
On remarque ensuite qu’il est possible de simplifier la partie condition, en effet si le premier argument du IF n’est pas une variable propositionnelle alors une des équivalences suivantes va s’appliquer :
| IF(⊤,P,Q)≡ P IF(⊥,P,Q)≡ Q IF(IF(B,P,Q),R,S)≡IF(B,IF(P,R,S),IF(Q,R,S)) |
On peut donc se ramener à des expressions conditionnelles dans lesquelles la condition est toujours une variable propositionnelle. On remarquera néanmoins que construire cette forme “simplifiée” peut faire grossir la taille de la formule de manière exponentielle.
En effet si on se donne des variables propositionnelles p,p1,…,pk,q1,…,qk, on peut construire une suite de formules
A0=p, An+1=IF(An,pn,qn). La formule An contient n connecteurs IF et chaque variable propositionnelle apparaît exactement une fois.
Si on veut simplifier An+1, on obtiendra la suite de transformations suivante :
| An+1 | = IF(An,pn,qn) = IF(IF(An−1,pn−1,qn−1),pn,qn) |
| | ≡IF(An−1,IF(pn−1,pn,qn),IF(qn−1,pn,qn)) |
| | ≡IF(An−2,IF(pn−2,IF(pn−1,pn,qn),IF(qn−1,pn,qn)),IF(pn−2,IF(pn−1,pn,qn),IF(qn−1,pn,qn)))
|
|
A chaque étape, on diminue de un le nombre de IF dans la condition mais on double le nombre de ceux qui apparaissent dans les branches et on en ajoute deux supplémentaires.
Un des enjeux sera donc de limiter cette explosion par le choix d’une méthode de construction et d’une représentation adéquate. Néanmoins, on gardera en
tête que le comportement exponentiel dans le pire des cas est de toute manière inévitable lorsqu’on veut résoudre des problèmes généraux du calcul propositionnel.
On s’intéresse dans la suite à des formules du calcul propositionnel, construit sur un ensemble de variables propositionnelles totalement ordonné.
Définition 1 (Arbre de décision binaire, BDT)
Un arbre de décision binaire (BDT) est un arbre binaire
dont les nœuds sont étiquetés par des variables propositionnelles et les feuilles sont formées des constantes booléennes V ou F.
On impose de plus que les variables propositionnelles des fils soient strictement plus grandes que celle du père.L’arbre de décision binaire définit une fonction booléenne sur l’ensemble des variables présentes dans l’arbre. Lorsque l’on passe un nœud étiqueté par la variable x, le sous arbre gauche correspond au cas où x a la valeur V et le sous-arbre droit au cas où x a la valeur F. Une branche de l’arbre définit donc une valeur pour les variables propositionnelles et la valeur de la fonction est déterminée par le booléen présent au niveau de la feuille. Comme toutes les variables ne sont pas forcément présentes dans une branche, celle-ci représente en général une valeur pour un ensemble d’arguments.
Exemple 12
Si on a deux variables propositionnelles p < q, on peut construire les arbres de décision binaire t et t′ suivant auquels sont associés la même fonction booléenne dont on donne le tableau :
| [.p [.q V V ] [.q F V ] ]
[.p V [.q F V ] ]
| |
On définit simplement de manière récursive la valeur vald(I,t) d’un arbre de décision binaire t dans une interprétation des variabbles propositionnelles I :
| | | vald(I,b)=b si b∈{V,F} |
| vald(I,IF(x,P,Q))=vald(I,P) si I(x)=V |
| vald(I,IF(x,P,Q))=vald(I,Q) si I(x)=F
|
|
Comme pour les formules ordinaires, pour une interprétation I et un arbre t, on notera I⊨ t la propriété vald(I,t)=V.
Exercice 5 (Arbre de décision binaire.)
-
Donner les équations récursives qui définissent une fonction form, qui prend en argument un BDT et renvoie une formule qui a la même table de vérité et qui n’utilise que des littéraux, des conjonctions et des disjonctions.
Transformer cette fonction pour obtenir directement un ensemble de clauses représentant la forme normale conjonctive.
- Définir par des équations récursives une fonction notd qui prend en argument un BDT t qui représente une formule A et renvoie un autre BDT qui représente la formule ¬ A.
- Définir par des équations récursives une fonction conjd qui prend en argument deux BDT t et u qui représentent respectivement les formules A et B et renvoie un autre BDT qui représente la formule A∧ B. On fera attention à respecter la contrainte sur l’ordre des variables propositionnelles dans les BDT.
- Que peut-on-dire des feuilles d’un BDT qui correspond à une formule valide ? satisfiable ? insatisfiable ?
- Proposer un algorithme pour trouver un modèle d’une formule.
Les arbres de décision binaire ont deux défauts : des arbres différents peuvent représenter des formules équivalentes (par exemple IF(x,P,P)≡ P) et leur taille est en général exponentielle en le nombre de variables propositionnelles.
Définition 2 (Diagramme de décision binaire, BDD)
Un diagramme de décision binaire (BDD) est obtenu à partir d’un arbre de décision en assurant de plus les conditions suivantes :
-
réduction: aucun nœud n’a deux fils identiques, cela correspond au fait que l’expression IF(p,A,A) est logiquement équivalente à A et donc on peut remplacer un nœud qui a deux fois le même fils par ce fils;
- partage: l’arbre est transformé en graphe orienté acyclique (DAG), c’est-à-dire que deux sous-arbres identiques sont partagés. Dans un graphe, il n’y a plus de notion de sous-arbre gauche et de sous-arbre droit : on étiquette donc les arcs par une valeur de vérité V ou F. Graphiquement on distingue par un arc plein le cas où la variable vaut V et par un arc pointillé le cas où la variable vaut F.
- variables ordonnées: comme dans les BDT, on va demander que les variables soient ordonnées : la variable d’un fils est toujours strictement supérieure à la variable du père, on parle alors de diagramme de décision binaire ordonné (ou OBDD).
Exemple 13
L’arbre donné dans l’exemple 12 correspond au diagramme suivant :
[level distance=10mm,
every node/.style=circle,draw,solid,inner sep=2pt
]
(pnode) p child[dashed] node q child[solid]
node[rectangle,draw] (F) F child node[rectangle,draw,solid]
(V) V ;
[sloped] (pnode) – (V);
Pour construire un OBDD à partir d’une formule propositionnelle P, il suffit de partir de la plus petite variable x qui apparaît dans la formule et de construire récursivement l’OBDD PV correspondant à la formule P[x← ⊤] pour la branche “vrai” et l’OBDD PF correspondant à la formule P[x← ⊥] pour la branche “faux”. Si les deux OBDDs sont les mêmes alors PV est le résultat attendu, sinon on introduit le nœud x avec un arc plein vers PV et un arc pointillé vers PF.
Exercice 6 - Construire les OBDDs des formules (z ⇔ t) puis (x ⇔ y) ∧ (z ⇔ t) en prenant comme ordre x < y < z < t.
- En partant des feuilles, annoter chaque noeud dans les deux OBDD précédents par une formule équivalente qui n’utilise que des littéraux et les symboles ∨ et ∧.
- Montrer que deux formules sont équivalentes si et seulement si elles sont représentées par le même OBDD. En déduire comment, étant donné un OBDD, on peut savoir si la formule associée est valide, satisfiable ou insatisfiable.
- Pour représenter un OBDD, on associe un numéro unique à chaque sommet du graphe et on utilise une table G qui permet de stocker pour chaque sommet la variable associée et les arêtes sortantes. On dispose des opérations suivantes :
-
noeud(G,n) : teste si n est un sommet du graphe qui correspond à un noeud interne;
- feuille(G,n) : teste si n est un sommet du graphe qui correspond à une feuille (V ou F);
- pour un nœud interne : var(G,n) donne la variable propositionnelle associée, vrai(G,n) est le numéro du sommet qui correspond au cas où la variable est vraie et
faux(G,n) est le numéro du sommet qui correspond au cas où la variable est
fausse;
- pour une feuille : valeur(G,n) renvoie un
booléen correspondant à la valeur V ou F de la feuille.
-
Exprimer à l’aide des fonctions ci-dessus, les propriétés sur la table G qui assurent que le graphe correspond bien à un OBDD : partage maximal, réduction et ordre sur les variables propositionnelles.
- Soit un graphe G correspondant à un OBDD et un sommet n, définir une fonction
form(G,n) qui calcule la formule logique associée au sommet n, expliquer comment exploiter le partage pour ne pas recalculer deux fois le même résultat.
- Expliquer comment construire une fonction if qui étant donnés un graphe G correspondant à un OBDD, une variable propositionnelle x et deux sommets n et m de G, renvoie un graphe G′ et un noeud p, tel que form(G′,p)≡IF(x,form(G,n), form(G,m)) et form(G′,k)=form(G,k) pour tous les sommets de G (G′ contient possiblement un sommet de plus que G, mais ne modifie pas les sommets de G). On utilisera une table T qui permet de retrouver si une formule est déjà représentée dans le graphe : il suffit de donner le nom de la variable et les sommets correspondant au cas vrai et au cas faux, si le nœud apparait dans le graphe, la table donnera le sommet correspondant.
- On veut compter le nombre de modèles d’une formule représentée par un OBDD.
-
Soit l’OBDD suivant sur les variables propositionnelles x1,x2,x3,x4,x5 :
[level distance=8mm,
every node/.style=circle,draw,solid,inner sep=2pt
]
x1
child [level distance=10mm] node (x3) x3
child [level distance=9mm] node (x4) x4
child [level distance=9mm] node[rectangle,draw] (V) V
child [level distance=10mm]node (x2) x2 edge from parent [dashed]
child [level distance=9mm]node (x5) x5 edge from parent [solid]
child[level distance=9mm]node[rectangle,draw] (F) F
;
[dashed] (x2) – (x3);
[dashed] (x3) – (x5);
[dashed] (x4) – (F);
[dashed] (x5) – (V);
annoter chaque nœud n du graphe pour donner le nombre d’interprétations concernant les variables plus grandes que celle du nœud n qui satisfont la formule associée à n.
- On suppose donnée une fonction indice qui calcule pour chaque sommet de l’OBDD un entier : si le sommet est un nœud, l’indice est la position de la variable correspondante dans l’ordre (la plus petite variable a le numéro 1) et si le sommet est une feuille, l’indice est n+1 avec n le nombre total de variables.
Construire une fonction nbsat qui étant donné un OBDD représenté par un graphe G et un sommet n, retourne le nombre de modèles de la formule en ne considérant que les variables plus grandes que celle du sommet.
- Sachant que la variable racine d’un OBDD n’est pas forcément la plus petite variable, en déduire le nombre de modèles de la formule en considérant toutes les variables.
3.3 Systèmes de déduction
On s’intéresse maintenant à la possibilité de déduire de manière
syntaxique qu’une formule P est une conséquence
logique d’un ensemble de formules E, c’est-à-dire que la
formule P sera vraie dans toute interprétation qui rend les
formules de E vraies.
Nous allons introduire des systèmes de déduction qui définissent des relations sur les formules en se donnant un certain nombre de règles du jeu, liées à leur structure logique.
Les relations peuvent porter sur les formules elle-mêmes ou bien sur une structure un peu plus compliquée appelée séquent qui prend en compte à la fois un ensemble d’hypothèses et une ou même un ensemble de conclusions.
Avant d’introduire les systèmes spécifiques à la logique, nous donnons le cadre général des définitions par règles d’inférence.
3.3.1 Préliminaires
Système et règles d’inférence
Les règles d’inférence sont une manière de définir une relation mathématique R qui est très utile en informatique théorique. Dans tout ce qui suit, on s’intéresse à des propriétés mathématiques générales et non pas à des formules de la logique (même si les notations peuvent se ressembler). Une relation n-aire R est juste un sous ensemble du produit de n ensembles A1×…× An.
Dans la suite on considère une relation sur un ensemble A qui pourra être choisi si nécessaire comme un ensemble produit. La relation est donc simplement un sous-ensemble R de A.
On écrira de manière générique R(t) la propriété qui dit que t∈ R.
On se donne donc un ensemble A, on veut définir une relation R sous-ensemble de A. L’idée est de caractériser la relation R par des conditions que cette relation R doit vérifier.
Ces conditions sont traditionnellement représentées par des règles d’inférence.
Une règle d’inférence se présente sous la forme d’une fraction :
Le dénominateur (aussi appelé la conclusion de la règle) est
forcément un cas particulier de la relation que l’on cherche à
définir. Le numérateur contient un nombre quelconque de conditions (que l’on appelera aussi les prémisses de la règle d’inférence).
La règle peut utiliser des variables mathématiques x1… xp, appelés paramètres.
L’interprétation de la règle est que pour n’importe quelles valeurs possibles de x1… xp, si les conditions P1… Pk sont vérifiées alors la propriété R(t) est également vérifiée.
S’il n’y a aucune condition k=0,
cela veut dire que R(t) est toujours vrai.
Par exemple on peut définir le fait qu’un nombre entier est pair avec les règles d’inférences suivantes :
Dans la deuxième règle, x est est un paramètre représentant n’importe quel entier, c’est-à-dire que la règle est valable si on remplace x par n’importe quel terme. Par exemple
mais aussi
.
Il y a plusieurs relations qui vérifient ces propriétés (par exemple l’ensemble des entiers ℕ). La relation définie par les règles d’inférence est par construction l’intersection de toutes les relations qui vérifient les conditions. Ce sera la la plus petite relation (au sens de l’inclusion) ayant cette propriété.
Le fait qu’une telle relation existe et a les bonnes propriétés est un théorème qui nécessite des conditions supplémentaires sur Pi.
Nous nous intéresserons au cas simple dans lequel chaque Pi est soit un cas particulier R(u) de la relation à définir, soit une condition auxiliaire qui ne parle pas de R.
Définition 1 (Relation définie par des règles d’inférences)
Soit un ensemble A. Une relation R sur A peut se définir par un système d’inférence qui est un ensemble fini de règles d’inférence.Chaque règle d’inférence est de la forme
où t,u1,…,un∈ A et P1,…,Pk sont des conditions auxiliaires qui ne mentionnent pas R.
La règle d’inférence peut être paramétrée par des variables mathématiques x1… xp.
Chaque règle d’inférence représente une condition sur la relation R qui s’énonce ainsi : pour n’importe quelles valeurs possibles de x1… xp, si les conditions R(u1)… R(un) et P1… Pk sont vérifiées alors la propriété R(t) est également vérifiée.
La relation R ainsi définie est la plus petite relation qui vérifie l’ensemble des conditions associées aux règles d’inférence.
Preuve:
Cette définition nécessite une preuve à savoir l’existence d’une plus petite relation qui vérifie les conditions associées aux règles d’inférence.
On note Cond(R) l’ensemble des conditions associées aux règles d’inférence de R et on note R0 l’intersection ∩{R⊆ A | Cond(R)} de toutes les relations qui vérifient la condition.
Cette intersection est bien définie car il y a au moins une relation qui vérifie la condition à savoir la relation qui correspond à l’ensemble A tout entier.
Il faut montrer que R0 vérifie les conditions.
Une première remarque est que par définition de l’intersection, on a que R0(t) est vérifié si et seulement si
R(t) est vérifié pour toutes les relations R qui vérifient Cond(R).
Soit une règle d’inférence
paramétrée par des variables x1… xp.
Soit donc x1… xp quelconques, on suppose que les prémisses P1… Pk sont vérifiées pour la relation R0 et on doit montrer que R0(t) est vérifié.
Par définition de l’intersection on doit montrer que R(t) est vrai pour n’importe quelle relation qui satisfait les conditions Cond(R).
Parmi les conditions que satisfait R on a la règle d’inférence
, donc pour montrer R(t), il suffit de montrer que les prémisses P1… Pk sont vérifiées pour la relation R.
Les prémisses soit ne mentionnent pas R soit sont de la forme R(u).
-
si la prémisse ne mentionne pas R, comme elle est vraie pour R0, elle est aussi
vraie pour R;
- si la prémisse est de la forme R(u), alors comme la prémisse est vraie pour R0 on a R0(u) est vérifié et comme R vérifie toutes les conditions, on a R0⊆ R et donc R(u) est aussi vrai.
On en déduit que R vérifie les prémisses de la règle donc aussi la conclusion et donc comme R(t) est vrai pour toute relation qui vérifie les conditions, on a aussi R0(t). Ce qui conclut la démonstration du fait que R0 vérifie les conditions des règles d’inférence.
□
Remarques :
Ce résultat se généralise au cas où les prémisses sont des propriétés croissantes de la relation à définir (c’est-à-dire que si on a une condition P[R] qui dépend de la relation R alors si R⊆ S et P[R] est vérifié, il en est de même de P[S]. Une condition pourrait donc être de la forme ∀ y, R(u)∨ B, voir faire apparaître la relation R à gauche d’un nombre pair de symboles d’implication.
Par contre la croissance des prémisses est essentielle.
Si on essaie de définir de la même manière une relation être pair avec les deux règles suivantes :
La relation “tout le temps vraie” (pair=ℕ) vérifie ces conditions, de même pour la relation “ëtre pair” qui contient tous les entiers pairs (pair={2k|k∈ℕ}) et qui vérifie les conditions. Mais de manière plus surprenante, la relation “ëtre 0 ou impair” qui contient 0 ainsi que tous les entiers impairs (pair={0}∪ {2k+1|k∈ℕ}) vérifie aussi les conditions.
Donc si on prend l’intersection de toutes les relations qui vérifient les conditions, il reste juste la relation qui contient 0. Mais cette relation ne vérifie pas les conditions puisque elle ne contient pas 1 et donc elle devrait contenir 1+1=2 ce qui n’est pas le cas.
Dans nos exemples les seules prémisses qui mentionnent la relation à définir R sont de la forme R(u) et donc ne présentent pas ce problème.
Point fixe de Tarski.
Le résultat précédent est un cas particulier d’un théorème plus général, appelé théorème de point fixe de Tarski (attribué à Bronisłav Knaster et Alfred Tarski), qui établit l’existence d’un point fixe pour toute fonction monotone sur un espace ayant de bonnes propriétés.
Proposition 1 (Théorème de point fixe de Tarski)
On se donne (E,≤) un ensemble muni d’une structure de treillis complet, c’est-à-dire que ≤ est un ordre partiel et que toute partie A⊆ E admet une borne supérieure notée sup(A) dans E.Toute fonction croissante de E dans E admet un plus petit et un plus grand point fixe.
Preuve:
Par définition la borne supérieure est le plus petit des majorants c’est donc un majorant (pour tout x∈ A, on a x≤ sup(A)) et c’est le plus petit donc si on a e∈ E qui est un majorant (pour tout x∈ A, on a x≤ e) alors sup(A)≤ e.
L’existence d’une borne supérieure implique l’existence d’une borne inférieure pour tout ensemble (la borne inférieure de l’ensemble A est la borne supérieure de l’ensemble des minorants de A), on la notera inf(A).
On regarde l’ensemble A={x∈ E|f(x)≤ x} et on pose a=inf(A).
Les propriétés de la borne inférieure sont
-
si f(x)≤ x alors a≤ x (minorant)
- si y est un minorant (y≤ x pour tout x tel que f(x)≤ x), alors y≤ a (plus grand des minorants)
La preuve suit alors les étapes suivantes :
□
Arbre de dérivation
Lorsque l’on introduit un système d’inférence pour définir une relation, on utilise ces mêmes règles d’inférence pour justifier que la relation est vérifiée.
De manière générale, une preuve de R(a) se construit par étapes comme une séquence de faits (dérivation)
de la forme R(b1),…,R(bn) où chaque R(bi) s’obtient par une règle dont les prémisses sont dans R(b1),…,R(bi−1). En pratique on représente la dérivation comme un arbre dont la racine est la conclusion et chaque nœud correspond à un cas particulier d’une règle d’inférence.
Définition 2 (Arbre de dérivation)
Etant donné un système d’inférence pour une relation R⊆ A, on construit un arbre de dérivation pour ce système. Les noeuds de cette arbre sont étiquetés par des instances de la relation de la forme R(a).Chaque noeud correspond à un cas particulier d’une règle d’inférence
.
C’est-à-dire qu’il existe des valeurs pour les paramètres x1…,xp de la règle pour lesquelles t=a.
On écrit
| R(b1)… R(bn) P′1… P′k |
|
| R(a) |
la règle obtenue pour ce cas particulier des paramètres.
Pour que la règle soit applicable, il faut que l’ensemble des conditions auxiliaires P′1… P′k soient vérifiées.
Un nœud correspondant à cette règle aura n fils (un fils par prémisse de la forme R(bi)), chaque fils est étiqueté par cette prémisse.
L’arbre est complet s’il n’y a plus de feuilles (application de règles sans prémisse portant sur R, c’est-à-dire n=0) et il constitue alors une preuve que la racine est dans la relation.
Un arbre incomplet constitue une preuve du fait que si l’ensemble des propriétés correspondant aux feuilles de l’arbre sont vérifiées alors la propriété à la racine de l’arbre est aussi vérifiée.
L’arbre se dessine en juxtaposant les règles d’inférence instanciées, il est recommandé de nommer chaque règle et de reporter le nom en marge de la barre de fraction. De même les conditions qui doivent être vérifiées peuvent être rappelées en annotation du nœud. On peut aussi noter les valeurs prises par les paramètres de la règle de manière à les reporter uniformément dans les prémisses et la conclusion.
Exercice 7 (Déplacement d’un robot)
On veut modéliser le déplacement d’un robot dans le plan. Les coordonnées sont données par des couples d’entiers naturels. Le robot part de la position (0,0). Les seuls déplacements possibles sont d’une case (x,y) à la case (x+1,y+2) ou bien à la case (x+2,y+1)-
Définir par un système d’inférence la relation pos sur ℕ×ℕ correspondant à toutes les positions accessibles au robot.
- Construire un arbre de dérivation pour montrer pos(3,3).
- Justifier que pos(1,1) implique pos(3,5).
Preuve par minimalité de la relation
Le fait que la relation définie est la plus petite qui satisfait les règles d’inférence, nous permet également de dériver un schéma de preuve puissant qui dit que si on se donne une autre relation S qui vérifie les mêmes conditions associées aux règle d’inférence que R alors
pour tout t, si R(t) on a aussi S(t). On appellera ce schéma de preuve, une preuve par minimalité de la définition de R.
Dans le cas de la définition de pair, cela se traduit par le principe suivant :
Proposition 2 (Principe de minimalité sur les entiers pairs.)
-
Soit φ(n) une propriété à montrer sur les entiers, si on peut démontrer les deux propositions suivantes :
-
φ(0) est vérifié;
- pour tout n tel que pair(n), si φ(n) est
vérifié alors φ(n+2) est vérifié;
- alors on peut en déduire que pour tout n tel que
pair(n) on a φ(n) est vérifié.
Par exemple on peut utiliser ce principe pour prouver que si n vérifie pair alors il existe k tel que n=2k. Il suffit de vérifier les deux conditions du principe précédent avec pour propriété φ(n), l’énoncé “il existe k tel que n=2k”, c’est-à-dire :
-
il existe k tel que 0=2k (il suffit de prendre k=0)
- soit n tel que pair(n), supposons qu’il existe k tel que n=2k, montrons qu’il existe k′ tel que n+2=2k′. Il suffit de prendre k′=k+1.
L’exemple pair est particulièrement élémentaire et on peut trouver d’autre formulations équivalentes sans utiliser de règles d’inférence comme ∃ k, n=2k ou bien n mod 2=0.
Définition 3 (Schéma général de minimalité)
Soit R⊆ A définie par un système d’inférence. Le schéma de preuve par minimalité pour la définition de R
-
Soit φ(x) une propriété paramétrée par x∈ A
- Pour chaque règle d’inférence de la relation R, de la forme
, dont les paramètres sont x1,…,xp, il faut vérifier que la propriété φ est préservée par la règle, ce qui s’écrit :
pour n’importe quelles valeurs des paramètres x1,…,xp qui vérifients les prémisses de la règle (on a R(u1)… R(un) et P1… Pk) et tels que φ(u1)… φ(un) sont vérifiés, alors φ(t) est vérifié
- Si on a vérifié toutes les conditions précédentes, alors φ(t) est vérifié pour tous les éléments t tels que R(t).
Exercice 8
On reprend la définition de l’exercice 7 des positions d’un robot.
-
Enoncer le principe de minimalité associé à cette définition.
- Utiliser ce principe pour montrer que pour tout x y, si pos(x,y)
alors x+y mod 3 = 0
- En déduire que pos(1,1) est faux
Les systèmes d’inférence sont utiles pour définir des relations générales qui ne sont pas des fonctions.
Par exemple, si on suppose donnée une relation ami(x,y) qui représente le fait que x a déclaré que y est son ami dans un réseau social.
Alors on peut simplement définir une relation reseau(x,y) qui représente le fait qu’il y a une chaîne d’amitiés entre x et y.
Il suffit de traduire les conditions suivantes :
-
Si x et y sont amis alors ils sont dans le même réseau.
- Si x et y sont dans le même réseau et y et z sont amis alors x et z sont dans le même réseau.
- Il n’y a pas d’autre manière d’être dans le même réseau : si quelqu’un est dans mon réseau, il est soit mon ami, soit l’ami de quelqu’un dans mon réseau
Ce qui s’exprime par les règles d’inférence suivantes :
| | | reseau(x,y) ami(y,z) |
|
| reseau(x,z) |
|
Il peut y avoir plusieurs systèmes d’inférence différents qui définissent la même relation (au sens où on peut prouver reseau(x,y) si et seulement si reseau1(x,y) si et seulement si reseau2(x,y)) :
| | | ami(x,y) reseau1(y,z) |
|
| reseau1(x,z) |
|
ou encore :
| | | reseau2(x,y) reseau2(y,z) |
|
| reseau2(x,z) |
|
Les systèmes d’inférence ont des applications en logique pour définir des systèmes de déduction, ils sont également beaucoup utilisés en informatique pour modéliser la sémantique des langages de programmation, par exemple les règles de typage ou les traductions entre langages en particulier dans le domaine de la compilation. C’est aussi une technique qui permet de modéliser des systèmes informatiques ayant des comportements non déterministes (systèmes parallèles et communicants).
Systèmes de déduction
On va s’intéresser ici à des systèmes d’inférence qui vont nous permettre de prouver la validité de formules en utilisant leurs propriétés syntaxiques. On parlera de système de déduction logique, ou système de preuve.
Lorsqu’on fait un raisonnement, on a pour habitude de travailler de manière générale avec un ensemble d’hypothèses Γ et une formule P.
Définition 4 (Séquent)
On appelle séquent un couple formé d’un ensemble fini de formules Γ (les hypothèses) et une formule P appelée la conclusion. On note le séquent Γ⊢ P.La formule associée au séquent P1,…,Pn ⊢ Q est définie comme (P1∧ … ∧ Pn)⇒ Q
Un séquent Γ⊢ P est valide si P est conséquence logique de Γ (Γ⊨ P) ou de manière équivalente si la formule associée au séquent est valide.
Notations associées aux séquents
Si Γ est un ensemble fini de formules {A1,…,An}, on écrit A1,…,An⊢ P pour la propriété Γ ⊢ P.
Si Γ est l’ensemble vide, on note simplement ⊢ P. Si Q est une formule, on note Γ,Q l’ensemble Γ auquel on a ajouté la formule Q soit Γ∪{Q} de même si Γ et Δ sont des ensembles finis de formules, on note Γ,Δ l’ensemble Γ∪Δ formé par leur union.
L’ensemble des variables libres d’un ensemble de formules Γ est par définition l’union des variables libres des formules de Γ, il est note Vl(Γ).
Séquents prouvables
Nous allons définir par des systèmes d’inférence des relations pour capturer l’ensemble des séquents “prouvables”. Traditionnellement, on n’introduit pas de notation supplémentaire. Ainsi suivant le contexte, la notation Γ ⊢ P représentera l’objet séquent (un couple formé d’un ensemble d’hypothèses et d’une conclusion) ou bien la propriété qui dit que ce séquent en prouvable dans le système considéré.
Un arbre de preuve pour un séquent Γ⊢ P est un arbre de dérivation complet qui établit que le séquent est prouvable.
Faire une preuve d’une formule P se fera en construisant un arbre de dérivation dont la racine sera le séquent ⊢ P (sans hypothèse).
On n’introduira évidemment que des systèmes corrects : tout séquent prouvable est valide et on cherchera à ce que les systèmes soient complets à savoir que tout séquent valide soit prouvable.
 Les règles d’inférence pour faire des preuves reposent sur la syntaxe des formules, ainsi il n’est pas correct de transformer dans un séquent une formule par une autre formule équivalente (sauf si une règle nous autorise explicitement à le faire).
Les règles d’inférence pour faire des preuves reposent sur la syntaxe des formules, ainsi il n’est pas correct de transformer dans un séquent une formule par une autre formule équivalente (sauf si une règle nous autorise explicitement à le faire).
3.3.2 Système de Hilbert
On peut définir un système simple pour dériver des formules valides dans une logique minimale (avec juste des variables propositionnelles et le connecteur ⇒). Soit Min l’ensemble des formules de la logique minimale. On définit une relation sur cet ensemble, qui va représenter des formules prouvables.
La relation que l’on définit est notée ⊢ P avec P∈Min.
Elle est donnée par le système d’inférence suivant qui comporte deux “axiomes” (des règles sans prémisses) et la règle de Modus Ponens :
| (K) | | (S) | |
|
| ⊢ (p⇒ q⇒ r)⇒ (p⇒ q) ⇒ (p⇒ r) |
| (mp) | |
Exemple 14
On peut établir dans ce système que ⊢ p⇒ p, en construisant l’arbre de dérivation suivant :
|
| | mp | | mp | | S | |
| |
| | ⊢ (p⇒ (p ⇒ p) ⇒ p)⇒ (p⇒ p ⇒ p) ⇒ (p⇒ p) |
|
| |
|
| |
| | ⊢(p⇒ p ⇒ p) ⇒ (p⇒ p) |
|
| |
|
| |
| | ⊢ p⇒ p |
|
Si on veut montrer que toute formule P telle que ⊢ P est prouvable est aussi valide (si ⊢ P alors ⊨ P) on va le faire en utilisant le principe de minimalité associé à la définition de ⊢.
Il nous suffit de montrer les trois propriétés, une pour chaque règle d’inférence pour n’importe quelles formules p, q et r.
-
⊨ p⇒ q⇒ p
- ⊨ (p⇒ q⇒ r)⇒ (p⇒ q) ⇒ (p⇒ r)
- si ⊨ p⇒ q et ⊨ p alors ⊨ q
ce qui se vérifie simplement.
On étend ce système au cas du raisonnement sous hypothèses. Les règles vues précédemment sont transformées pour intégrer les hypothèses. Une règle est ajoutée qui dit que toute formule qui apparaît dans les hypothèses Γ est prouvable.
| (hyp) | | (K) | | (S) | |
|
| Γ⊢ (p⇒ q⇒ r)⇒ (p⇒ q) ⇒ (p⇒ r) |
| (mp) | |
Si une formule est prouvable à partir d’hypothèses Γ est est a fortiori prouvable si on ajoute des hypothèses. Cette propriété essentielle s’appelle l’affaiblissement.
Proposition 3 (Affaiblissement des hypothèses)
Si Γ⊢ p, alors pour tout ensemble Δ tel que Γ⊆ Δ, on a Δ⊢ p.Preuve:
La preuve se fait simplement en utilisant le principe de minimalité associé à la définition. Soit Γ et Δ deux ensembles de formules telles que Γ⊆ Δ, la propriété à prouver est Δ⊢ p.
On vérifie simplement que la propriété Δ⊢ p est bien stable pour les quatre règles d’inférence qui définissent la relation Γ⊢ p.
Le seul cas non trivial est celui de la règle hypothèse pour laquelle on a p∈Γ, comme Γ⊆ Δ, on a aussi p∈Δ, on en déduit Δ⊢ p.
□
Une autre propriété d’affaiblissement qui nous sera utile est la suivante.
Proposition 4 (Affaiblissement de la conclusion)
Si Γ⊢ p alors Γ⊢ q⇒ p.Preuve:
C’est une simple déduction sous hypothèse :
□
Proposition 5 (Théorème de déduction)
Soit Γ un ensemble de formules et p,q deux formules. On a Γ,p⊢ q si et seulement si Γ ⊢ p⇒ q.Preuve:
-
Si Γ ⊢ p⇒ q alors
-
par le théorème d’affaiblissement des hypothèses, on a aussi Γ,p ⊢ p⇒ q
- par la règle hypothèse, Γ,p ⊢ p
- par la règle modus-ponens, on a donc Γ,p ⊢ q
- Réciproquement, on suppose que Γ,p⊢ q on va montrer Γ ⊢ p⇒ q en utilisant le principe de minimalité associé à la définition de la relation Γ,p⊢ q.
-
règle hypothèse Γ,p ⊢ q avec q∈ Γ,p :
-
soit q∈Γ et alors on a Γ⊢
q et donc par affaiblissement de la conclusion on a
Γ⊢ p⇒ q,
- si q=p alors on obtient
la dérivation de Γ⊢ p⇒ p comme dans
l’exemple 14.
- pour les deux règles S et K, elles sont dérivables quelque soit l’ensemble d’hypothèses, il suffit donc à chaque fois d’appliquer la proposition d’affaiblissement de la conclusion
- pour la règle modus ponens qui est
| Γ,p ⊢ r⇒ q Γ,p⊢ r |
|
| Γ,p ⊢ q |
on a donc Γ ⊢ p⇒ r⇒ q et Γ⊢ p⇒ r,
on construit alors la dérivation suivante :
| mp | | mp | | S | |
| |
| | Γ⊢ (p⇒ r⇒ q) ⇒ (p⇒ r)⇒ (p⇒ q) |
|
Γ⊢ p⇒ r⇒ q |
|
| |
| | Γ⊢ (p⇒ r) ⇒ p⇒ q |
|
Γ⊢ p⇒ r |
|
| |
| | Γ⊢ p⇒ q |
|
□
Dans le système de Hilbert, la relation de déduction est définie avec un ensemble fixe d’hypothèses, le théorème de déduction peut se voir comme une règle “dérivée” qui transforme simultanément l’ensemble des hypothèses et la conclusion.
L’idée des calculs de séquents est d’intégrer dans les règles d’inférence des manipulations sur l’ensemble des hypothèses. Il en existe plusieurs variantes. Nous présentons ici la déduction naturelle et le calcul des séquents à conclusions multiples, deux systèmes qui ont été introduits par Gerhart Gentzen.
3.3.3 Déduction naturelle
Nous donnons ici les principes de base de la déduction naturelle, un système qui est proche du raisonnement mathématique usuel.
Nous allons définir une relation qui correspond au sous-ensemble des séquents “prouvables en déduction naturelle”. Dans cette section, la notation Γ ⊢ P représente soit l’objet séquent, soit la propriété qui dit que ce séquent en prouvable en déduction naturelle.
Nous présentons chacune
des règles
sous forme de règles d’inférence
qui permet de construire un arbre de preuve dont la racine (en
bas) représente le séquent que l’on cherche à justifier et les
feuilles sont des conditions suffisantes.
Règles de base
Une première série de règles permet de
terminer une preuve dans les cas “élémentaires” :
-
Hypothèse : si la conclusion fait partie des hypothèses alors la preuve est terminée.
- Si la conclusion est la formule atomique toujours vraie alors la preuve est terminée.
Règles d’introduction
Les règles suivantes expliquent comment ramener la preuve d’une formule à des preuves de certaines de ses sous-formules. On les appelle des règles d’introduction :
-
Si on veut prouver A∧ B alors on peut se ramener à démontrer d’une part la conclusion A d’autre part la conclusion B. Les hypothèses ne changent pas.
- Si on veut montrer A∨ B alors on a deux possibilités : on peut se ramener à démontrer la conclusion A avec les mêmes hypothèses ou bien on peut se ramener à démontrer la conclusion B avec les mêmes hypothèses.
Attention l’utilisation de l’une ou l’autre de ces règles peut ne pas aboutir car il y a des situations où A∨ B est vrai sans qu’on puisse conclure que A est vrai ou B est vrai … Par exemple, on peut déduire
B∨ A à partir de l’hypothèse A∨ B mais à partir de l’hypothèse A∨ B, on ne peut déduire ni B ni A.
- Si on veut montrer ¬ A alors on peut se ramener à démontrer une contradiction en ajoutant la propriété A dans les hypothèses.
- Si on veut montrer A⇒ B alors on peut se ramener à démontrer la conclusion B en ajoutant la propriété A dans les hypothèses.
- Si on veut montrer ∀ x, P alors on se ramène à prouver P pour un x quelconque. La contrainte x quelconque impose que le nom x ne soit pas déjà utilisé ailleurs et donc qu’il ne soit pas libre dans les hypothèses. On peut toujours se ramener à ce cas là, car si x était utilisé dans les hypothèses, comme x est lié dans la formule ∀ x, P, on peut procéder à un renommage : on choisit un nom y qui n’apparait pas par ailleurs, et on remplace ∀ x, P par ∀ y, P[x← y]
- Si on veut montrer ∃ x, P alors il suffit de produire un objet t, et on se ramène à prouver P[x← t]. Attention si on choisit mal l’objet t, le séquent en prémisse peut ne pas être prouvable.
Ces règles sont suffisantes pour prouver les propriétés suivantes (sans hypothèses) :
mais elles ne sont pas suffisantes pour montrer une propriété comme
(A ∧ B) ⇒ (A ∨ B). En effet elles se contentent
d’ajouter des connecteurs dans la conclusion, nous allons expliquer
maintenant des règles qui permettent d”’enlever” des connecteurs.
Règles d’élimination
Les règles suivantes expliquent comment utiliser une preuve d’une formule en fonction du connecteur principal de cette formule. On appelle ces règles des règles d’élimination.
-
Si on a prouvé l’absurde (ce qui signifie que les hypothèses sont contradictoires) alors avec les mêmes hypothèses, on peut prouver n’importe quoi:
- Si on a prouvé ¬ A et que l’on sait aussi prouver A alors on a une contradiction et donc on peut prouver n’importe quoi:
- Si on a prouvé A ∧ B alors on peut en déduire A et on peut en déduire B:
- Si on a prouvé A ∨ B alors on peut raisonner par cas, en considérant deux instances de notre problème, l’un avec l’hypothèse A en plus et l’autre avec l’hypothèse B en plus:
| (∨ E) | | Γ ⊢ A ∨ B Γ,A ⊢ C Γ,B ⊢ C |
|
| Γ ⊢ C |
|
- Si on a prouvé A ⇒ B et que l’on peut prouver A alors on peut en déduire B, on retrouve la règle de Modus-Ponens:
- Si on a prouvé ∀ x,P, alors on peut en déduire que P est vrai pour n’importe quel objet t:
- Si on a prouvé ∃ x,P, alors on peut donner un nom à cet objet (que l’on ne connait pas) et ajouter l’hypothèse que cet objet satisfait P. Comme on ne connait rien de l’objet (sauf qu’il existe), le nom que l’on choisit doit être neuf et donc ne doit pas être déjà utilisé. Comme le nom x est lié dans ∃ x,P, on peut toujours procéder à un renommage
∃ y,P[x← y] pour choisir un nom nouveau qui convient.
| (∃ E) | | Γ ⊢ ∃ x,P Γ,P ⊢ C x ∉Vl(Γ,C) |
|
| Γ ⊢ C |
|
Raisonnement par l’absurde
Enfin, les règles précédentes ne suffisent pas à prouver toutes les
formules valides (par exemple A∨¬ A), il faut y ajouter le schéma de raisonnement
classique qui capture ce que l’on appelle le
raisonnement par l’absurde. Si on veut prouver A alors
on peut supposer ¬ A et en déduire une contradiction.
Règles dérivées
On remarque que si une formule A est une conséquence
d’hypothèses Γ alors a fortiori A est une
conséquence d’un ensemble d’hypothèses Δ qui contient
les hypothèses de Γ. C’est vrai pour la règle hypothèse, puis c’est
préservé par toutes les règles.
Ce résultat peut s’énoncer de la manière suivante :
Proposition 6 (Affaiblissement des hypothèses)
Si Γ ⊢ A et Γ ⊆ Δ alors
Δ ⊢ A
On peut donc oublier des hypothèses inutiles lorsque l’on construit une
preuve. Attention par contre à ne pas supprimer d’hypothèse qui peuvent être nécessaires pour compléter la preuve.
À partir des règles de base que l’on s’est données, on peut déduire d’autres schémas de preuve naturels que l’on pourra utiliser librement.
-
Preuve par coupure
C’est une simple conséquence des règles pour le connecteur ⇒
- Pour chaque connecteur logique, on peut spécialiser la règle d’élimination au cas où la formule à éliminer est déjà dans les hypothèses. Cela remplace une branche de l’arbre qui se conclurait par l’utilisation d’une règle hypothèse par une condition de la forme P∈Γ qui se vérifie tivialement. Pour la conjonction et la quantification universelle, la forme de la règle est légèrement différente, elle nous permet d’enrichir l’ensemble des hypothèses pour continuer la preuve.
-
Contradiction : (⊥ H)
- Negation : (¬ H)
- Conjonction : (∧ H)
- Disjonction : (∨ H)
| Γ,A ⊢ C Γ,B ⊢ C A∨ B ∈ Γ |
|
| Γ ⊢ C |
- Implication : (⇒ H)
| Γ,B ⊢ C Γ ⊢ A A ⇒ B ∈ Γ |
|
| Γ ⊢ C |
- Quantification universelle : (∀ H)
| Γ,P[x← t] ⊢ C ∀ x, P ∈ Γ |
|
| Γ ⊢ C |
- Quantification existentielle : (∃ H)
| Γ,P ⊢ C x ∉Vl(Γ,C) ∃ x, P ∈ Γ |
|
| Γ ⊢ C |
Récapitulatif des règles de la déduction naturelle
|
| | hypothèse | |
| absurde | |
| | introduction | elimination | élimination hypothèse (dérivée) |
| ⊥ | | | |
| ⊤ | | | |
| ¬ | | | |
| ∧ | | | |
| ∨ | | | Γ ⊢ A ∨ B Γ,A ⊢ C Γ,B ⊢ C |
|
| Γ ⊢ C |
| | Γ,A ⊢ C Γ,B ⊢ C A∨ B ∈ Γ |
|
| Γ ⊢ C |
|
| ⇒ | | | | Γ,B ⊢ C Γ ⊢ A A ⇒ B ∈ Γ |
|
| Γ ⊢ C |
|
| ∀ | | | | Γ,P[x← t] ⊢ C ∀ x, P ∈ Γ |
|
| Γ ⊢ C |
|
| ∃ | | | Γ ⊢ ∃ x,P Γ,P ⊢ C x ∉Vl(Γ,C) |
|
| Γ ⊢ C |
| | | | Γ,P ⊢ C x ∉Vl(Γ,C) ∃ x, P ∈ Γ |
|
| Γ ⊢ C |
|
|
|
| |
|
Exemple
Dérivation de ¬ A ∨ B ⇒ A ⇒ B.
Au départ il n’y a pas d’hypothèse, le séquent à montrer est ⊢ ¬ A ∨ B ⇒ A ⇒ B.
On commence par faire des introductions du connecteur ⇒, on a donc deux hypothèses ¬ A ∨ B, A et on doit montrer B.
On raisonne par cas sur la preuve de ¬ A ∨ B (vraie par hypothèse).
-
On doit montrer B sous les hypothèses ¬ A ∨ B, A,¬ A
ce qui est vrai par contradiction (A et ¬ A sont vrais par hypothèse);
- On doit aussi montrer B sous les hypothèses ¬ A ∨ B, A,B
vrai par hypothèse.
L’arbre de preuve correspondant s’écrit :
Exercice 9 (Preuve en déduction naturelle)
Construire des démonstrations en déduction naturelle des formules et séquents suivants :
-
A ⇒ (B ⇒ A)
- (A ⇒ ¬ A) ⇒ ¬ A
- (∃ x,P(x)) ⇒ ¬ ∀ x,¬ P(x)
- ¬ ∃ x, P(x) ⊢ ∀ y, ¬ P(y)
Exercice 10 (Raisonnement par l’absurde en déduction naturelle)
Construire des arbres de dérivation pour faire les preuves en déduction naturelle des séquents suivants :
-
P ⊢ ¬¬ P et ¬¬ P ⊢ P (pour ce séquent, commencer par la règle de raisonnement par l’absurde)
- ¬(¬ P ∨ P) ⊢ ¬ P, en déduire en utilisant le raisonnement par l’absurde une dérivation de ⊢ ¬ P∨ P
- Paradoxe du buveur :
B =def ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)).
On suppose l’existence dans le langage d’un objet a.
On procèdera en démontrant d’abord les séquents
∀ x,¬ P(x) ⊢ B et
∃ x, P(x) ⊢ B et on pourra utiliser les séquents démontrés précédemment ainsi que la règle de coupure.
Déduction naturelle et programmation fonctionnelle
La déduction naturelle a des liens très étroits avec la programmation fonctionnelle typée. Cette correspondance est connue sous le nom d’isomorphisme de Curry-Howard. Plus précisément on peut faire correspondre les formules logiques avec des types. Par exemple l’implication A⇒ B correspond au type des fonctions de A dans B et la conjonction A∧ B correspond au type des paires formées d’élément de A et de B. Les hypothèses du séquent correspondent aux types des variables du programme. Chaque règle de preuve correspond à une construction de programme. Ainsi une preuve d’un séquent va correspondre à un programme bien typé.
Les calculs qui peuvent se faire dans le langage de programmation correspondent à des transformations de preuves.
Le fait que les constructions de programmes fonctionnels soient plus sûres que leur correspondant impératifs ou objets et que leur preuve se fasse plus simplement est lié à cette similarité avec nos modes de raisonnement usuels. Néanmoins, afin de permettre l’expression de l’ensemble des fonctions calculables, les langages de programmation autorisent des constructions récursives générales et boucles non bornées. Les méthodes de peuves sont elles beaucoup plus restrictives afin de rester correctes.
L’isomorhisme de Curry-Howard est également à la base d’un système de preuve interactif comme Coq (ou Lean). La preuve est représentée par un terme fonctionnel qui doit satisfaire des règles de typage pour garantir la correction de la preuve.
3.3.4 Calcul des séquents multi-conclusions
Les règles de bases de la déduction naturelle permettent de faire naviguer des formules entre hypothèse et conclusion mais ne transforment pas la structure des formules dans les hypothèses. Or de telles règles sont utiles (nous les avons d’ailleurs fait apparaître comme des règles dérivées).
Par ailleurs la déduction naturelle repose sur un certain nombre de règles qui ne sont pas “inversibles” c’est-à-dire que la conclusion peut être vraie sans que les prémisses le soient. C’est le cas des règles d’introduction de la disjonction et de l’existentielle ou des règles d’élimination de la conjonction, de la quantification universelle et de l’implication.
L’utilisation de ces règles peut nous mener à des impasses. L’utilisation des règles d’élimination d’hypothèses pour la conjonction et la quantification universelle permet de traiter ces connecteurs sans perdre dinformation.
| ∀ H | | Γ,P[x← t] ⊢ C ∀ x, P ∈ Γ |
|
| Γ ⊢ C |
|
Mais cela ne résoud pas les questions de la disjonction, de l’existentielle et de l’implication.
On voit qu’il y a une disymétrie dans les séquents entre les hypothèses qui comportent plusieurs formules et la conclusion qui est limitée à une seule formule. L’idée du calcul des séquents est d’autoriser aussi un ensemble de formules à droite du symbole ⊢.
Définition 5 (Séquent à conclusions multiples)
On appelle séquent à conclusions multiples (ou séquent multi-conclusions) un couple formé de deux ensembles fini de formules Γ (les hypothèses) et Δ (les conclusions). On note le séquent Γ⊢ Δ.La formule associée au séquent multi-conclusions P1,…,Pn ⊢ Q1,…,Qp est définie comme (P1∧ … ∧ Pn)⇒ (Q1∨…∨ Qp). Si Δ=∅ (p=0) alors (Q1∨…∨ Qp) est par définition la formule ⊥ et la formule associée au séquent s’écrit (P1∧ … ∧ Pn)⇒ ⊥ ce qui est équivalent à ¬ (P1∧ … ∧ Pn).
Un séquent Γ⊢ Δ est valide si et seulement si la formule associée au séquent est valide ou, de manière équivalente, si pour toute interprétation I telle que I⊨Γ, il existe P∈Δ tel que I⊨ P.
On voit donc que l’ensemble des hypothèses à gauche du signe ⊢ est interprété comme une conjonction (toutes les hypothèses sont vraies) alors que l’ensemble des conclusions à droite du signe ⊢ est interprété comme une disjonction (au moins une des conclusions est vraie).
Les règles vont alors pouvoir prendre une forme symétrique entre gauche et droite. Chaque règle porte sur une des formules dans les hypothèses (on dit que c’est une règle gauche) ou dans les conclusions (on dit que c’est une règle droite) et va éliminer le connecteur ou quantificateur principal de cette formule pour se ramener à un ou plusieurs séquents à prouver.
Nous appellerons système G le système de déduction défini par l’ensemble des règles suivantes.
Règles du système G
Les règles permettent de décomposer les connecteurs soit dans la partie gauche du séquent, soit dans la partie droite.
On utilise des lettres grecques Γ, Δ pour représenter des ensembles arbitraires (finis) de formules.
On rappelle que l’ordre des formules n’intervient pas dans la définition d’un ensemble, ainsi les ensembles A,B,C et C,A,B sont égaux.
Un premier jeu de règles permet de conclure une preuve dans des cas triviaux (une contradiction dans les hypothèse, une propriété triviale dans les conclusion ou bien une conclusion qui est également une hypothèse):
Nous donnons ensuite les règles pour chaque connecteur : on retrouve la règle
Jok qui est la règle gauche de ⊥ et la règle Triv qui est la règle droite de ⊤.
|
| | | gauche | droite |
| ⊥ | | |
| ⊤ | | |
| ¬ | | |
| ∧ | | | Γ ⊢ Δ,A Γ ⊢ Δ,B |
|
| Γ ⊢ Δ,A∧ B |
|
| ∨ | | A,Γ ⊢ Δ B,Γ ⊢ Δ |
|
| A∨ B,Γ ⊢ Δ |
| |
| ⇒ | | Γ ⊢ Δ,A B,Γ ⊢ Δ |
|
| A⇒ B,Γ ⊢ Δ |
| |
| ∀ | | P[x← t],(∀ x,P),Γ ⊢ Δ |
|
| (∀ x,P),Γ ⊢ Δ |
| | Γ ⊢ Δ,P x ∉Vl(Γ,Δ) |
|
| Γ ⊢ Δ,(∀ x,P) |
|
| ∃ | | P,Γ ⊢ Δ x ∉Vl(Γ,Δ) |
|
| (∃ x,P),Γ ⊢ Δ |
| | Γ ⊢ Δ,(∃ x,P),P[x← t] |
|
| Γ ⊢ Δ,(∃ x,P) |
|
| |
|
Exemple 15 (Preuve propositionnelle en calcul des séquents)
On peut montrer ¬ (A ∧ B) ⊢ ¬ A ∨ ¬ B.
|
| | ∨ d | |
| |
| | ¬ (A ∧ B) ⊢ ¬ A ∨ ¬ B |
|
Exemple 16 (Preuves avec quantificateurs en calcul des séquents)
-
∃ x,(p(x)∨ q(x)) ⊢ (∃ x,p(x)) ∨ (∃ x,q(x))
|
| | ∨ d | | ∃ g | | ∨ g | | ∃ d | | hyp | |
| |
| | p(x) ⊢ p(x),(∃ x,p(x)),(∃ x,q(x)) |
|
| |
| | p(x) ⊢ (∃ x,p(x)),(∃ x,q(x)) |
|
| | | ⋮ |
| |
| | q(x) ⊢ (∃ x,p(x)),(∃ x,q(x)) |
|
|
| |
| | p(x)∨ q(x) ⊢ (∃ x,p(x)),(∃ x,q(x)) |
|
| |
| | ∃ x,(p(x)∨ q(x)) ⊢ (∃ x,p(x)),(∃ x,q(x)) |
|
| |
| | ∃ x,(p(x)∨ q(x)) ⊢ (∃ x,p(x)) ∨ (∃ x,q(x)) |
|
- ¬(∃ y,p(y)) ⊢ ∀ x,¬ p(x)
|
| | ¬ g | | ∀ d | | ¬ d | | ∃ d | | hyp | |
| |
| | p(x) ⊢ p(x),(∃ y,p(y)) |
|
| |
| | p(x) ⊢ ∃ y,p(y) |
|
| |
| | ⊢ (∃ y,p(y)),¬ p(x) |
|
| |
| | ⊢ (∃ y,p(y)),(∀ x,¬ p(x)) |
|
| |
| | ¬(∃ y,p(y)) ⊢ ∀ x,¬ p(x) |
|
Propriétés du Calcul des séquents
On établit simplement des propriétés sur la structure des preuves. Un séquent prouvable le reste si on ajoute des hypothèses ou des conclusions.
Proposition 7 (Affaiblissement)
Si Γ ⊢ Δ alors Γ,Γ′ ⊢ Δ,Δ′
Preuve:
On utilise une preuve par minimalité de la définition de Γ ⊢ Δ.
□
Si un séquent contient des variables libres et est prouvable alors il en est de même pour le séquent dans lequel la variable libre a été remplacée par un terme arbitraire.
Proposition 8 (Substitution)
Si Γ ⊢ Δ alors Γ[x← t] ⊢ Δ[x← t]
Preuve:
On utilise une preuve par minimalité de la définition de Γ ⊢ Δ.
□
Une autre propriété importante est que toutes les règles sont
inversibles c’est-à-dire qu’une interprétation rend vrai un séquent en
conclusion d’une règle si et seulement si elle rend vrais les séquents
qui apparaissent dans les prémisses.
Proposition 9
Les règles du système G sont correctes et inversibles.
Preuve:
On regarde les règles une par une en utilisant les propriétés des connecteurs et quantificateurs.
-
On peut se ramener à la validité des formules assossiées.
Si Γ=A1,…,An on note M la formule A1∧ … ∧ An et si Δ=B1,…,Bp on note P la formule
B1 ∨ … ∨ Bp.
Si on s’intéresse à la règle gauche de l’implication :
| Γ ⊢ Δ, A Γ,B ⊢ Δ |
|
| Γ,A⇒ B ⊢ Δ |
Les prémisses se traduisent par les formules
M ⇒ P ∨ A et B ∧ M ⇒ P
la conclusion se traduit par la formule
(A⇒ B) ∧ M ⇒ P
On vérifie que les formules (M ⇒ P ∨ A) ∧ (B ∧ M ⇒ P) et
(A⇒ B) ∧ M ⇒ P sont équivalentes (par exemple à l’aide de tables de vérité).
Une autre manière de raisonner est d’analyser directement la valeur de vérité d’un séquent. Un séquent est faux dans une interprétation, si et seulement si toutes les hypothèses sont vraies et toutes les conclusions sont fausses.
On peut donc faire directement les tables de vérité des trois séquents qui apparaissent dans la règle gauche de l’implication et on remarque que le séquent conclusion est vrai si et seulement si les deux séquents de prémisses sont vrais.
|
| | Γ | Δ | A | B | Γ ⊢ Δ, A | Γ,B ⊢ Δ | Γ,A⇒ B ⊢ Δ |
| F | _ | _ | _ | V | V | V |
| V | V | _ | _ | V | V | V |
| V | F | F | _ | F | _ | F |
| V | F | V | V | V | F | F |
| V | F | V | F | V | V | V |
| |
|
- Pour les règles des quantificateurs
|
(∀ g) | | P[x← t],(∀ x,P),Γ ⊢ Δ |
|
| (∀ x,P),Γ ⊢ Δ |
| (∃ d)
| | Γ ⊢ Δ,(∃ x,P),P[x← t] |
|
| Γ ⊢ Δ,(∃ x,P) |
|
on remarque qu’elles sont inversibles (cas particulier d’affaiblissement). On peut donc utiliser plusieurs fois le ∀ en hypothèse ou proposer plusieurs témoins pour un ∃ en conclusion.
□
 Des présentations alternatives du calcul des séquents utilisent plutôt des multi-ensembles (des éléments peuvent apparaître plusieurs fois) à la fois dans les hypothèses et les conclusions. Cela nécessite d’introduire une règle explicite dite de contraction qui remplace deux formules égales par une seule. Cela a un impact sur les règles ∀ g et ∃ d dans lesquels les formules ∀ x,P,∃ x,P ne sont pas reportées systématiquement dans les prémisses, l’utilisateur doit explicitement avoir recours à la contraction pour garder la formule quantifiée dans le séquent. Notre formulation garantit que toutes les règles sont inversibles (pas de perte d’information).
Des présentations alternatives du calcul des séquents utilisent plutôt des multi-ensembles (des éléments peuvent apparaître plusieurs fois) à la fois dans les hypothèses et les conclusions. Cela nécessite d’introduire une règle explicite dite de contraction qui remplace deux formules égales par une seule. Cela a un impact sur les règles ∀ g et ∃ d dans lesquels les formules ∀ x,P,∃ x,P ne sont pas reportées systématiquement dans les prémisses, l’utilisateur doit explicitement avoir recours à la contraction pour garder la formule quantifiée dans le séquent. Notre formulation garantit que toutes les règles sont inversibles (pas de perte d’information).
Proposition 10 (Propriétés de la sous-formule)
toutes les formules qui apparaissent dans un arbre de preuve de Γ ⊢ Δ sont des sous-formules de Γ,Δ
(avec la définition que P[x← t] est une sous-formule de ∀ x,P et de ∃ x,P )
Ce système a de bonnes propriétés pour l’automatisation du
raisonnement dans le cas propositionnel. En effet chaque séquent qui apparaît en prémisse d’une
règle d’inférence contient moins de connecteurs logiques que celui qui
est en conclusion et donc le processus qui consiste à appliquer les
règles logiques s’arrête forcément. La profondeur de l’arbre est au
maximum égale au nombre de symboles dans le séquent. Nous reviendrons sur ce point dans le chapitre ??
Règle de coupure
Définition 6 (Règle de coupure) On peut ajouter au système la règle dite de coupure.
| Γ ⊢ Δ,A Γ′,A ⊢ Δ′ |
|
| Γ,Γ′ ⊢ Δ,Δ′ |
|
Cette règle est correcte, réversible mais elle ne préserve pas
la propriété de la sous formule.
Un théorème établit que la règle de coupure est redondante :
Proposition 11 (Elimination des coupures)
Si Γ⊢ Δ en utilisant la règle de coupure alors
Γ⊢ Δ sans la règle de coupure.
Preuve: La preuve se fait en transformant les coupures pour faire “diminuer” leur taille. Elle est assez technique puisqu’il faut explorer tous les cas, de plus l’argument de terminaison n’est pas immédiat. Nous donnons ici quelques cas spécifiques.
-
Cas d’une règle hypothèse
| cut | Γ0,P⊢ Δ,P
Γ′,P⊢ Δ′ |
| |
| | Γ0,P,Γ′⊢ Δ,Δ′ |
| |
se transforme en un
affaiblissement
- Interaction règles gauche/droite P=∀ x, Q, x∉Vl(Γ,Δ)
| cut | |
| | ∀ g | Γ′,(∀ x, Q),Q[x← t]⊢ Δ′ |
| |
| | Γ′,(∀ x, Q)⊢ Δ′ |
|
|
| |
| | Γ,Γ′⊢ Δ,Δ′ |
|
se transforme en
| cut | | Γ⊢ Δ,Q[x← t]
| | cut | Γ⊢ Δ,(∀ x,Q)
Γ′,(∀ x, Q),Q[x← t]⊢ Δ′
|
| |
| | Γ′,Q[x← t]⊢ Δ′ |
|
|
| |
| | Γ,Γ′⊢ Δ,Δ′ |
|
□
Raisonnement par l’absurde
Contrairement au cas de la déduction naturelle, il n’est pas nécessaire d’ajouter une règle pour traiter les preuves par l’absurde. Celles-ci se font avec les règles standard mais tirent partie de la présence de plusieurs formules de conclusion et de la possibilité de commencer à décomposer une des conclusions et d’utiliser les éléments collectés pour établir une autre des conclusions.
Exemple 17 (Preuve du tiers exclu) Ceci est illustré sur la preuve de ⊢ ¬ P∨ P. Après avoir coupé la disjonction en deux conclusions, on commence par essayer de prouver ¬ P, on suppose donc que P est vrai et on devrait établir une contradiction, mais on a aussi la possibilité de s’attaquer à une autre des conclusions, ici P qui permet de conclure.
Exercice 11 (Preuve en calcul des séquents)
Prouver en utilisant les règles du calcul des séquents les propriétés suivantes :
-
A ⇒ (B ⇒ A)
- (¬ A ⇒ A) ⇒ A
- ¬ ∀ x,¬ P(x)⊢ ∃ x,P(x)
- P ⊢ ¬¬ P et ¬¬ P ⊢ P
- Paradoxe du buveur :
∃ x, (P(x) ⇒ ∀ y, P(y)).
Le calcul des séquents à conséquences multiples nous fournira directement une procédure de décision de la validité pour les formules propositionnelles.
Complétude
Nous avons construit des systèmes de preuves pour des calculs des séquents. Ces systèmes sont corrects dans le sens ou si Γ ⊢ P alors Γ⊨P.
Le théorème de complétude de Gödel nous dit que la réciproque est vraie c’est-à-dire que si une formule est valide alors elle est démontrable dans un système de déduction (la déduction naturelle ou le calcul des séquents sont deux tels systèmes).
Ce théorème reste vrai quand on raisonne dans une théorie donnée. Nous ferons dans le chapitre suivant la preuve pour le cas propositionnel. L’extension pour le calcul des séquents au premier ordre est plus technique (voir par exemple []).
Déduction naturelle et calcul des séquents
Nous avons présenté deux systèmes de preuve pour raisonner sur des séquents. Il n’est pas très difficile de tranformer les preuves entre ces deux systèmes. On établit les deux résultats suivants :
-
Si Γ ⊢ P en déduction naturelle alors Γ ⊢ P en calcul des séquents
- Si Γ ⊢ Δ en calcul des séquents alors Γ,¬ Δ ⊢ ⊥ en déduction naturelle avec la règle de raisonnement par l’absurde.
Dans les deux cas, on raisonne par minimalité de la définition des séquents prouvable dans un système en montrant que chaque règle d’un système peut se dériver dans l’autre système.
Conclusion
Cette partie nous a permis d’introduire la notion de système de preuves pour la logique et la structure de séquents qui généralise la notion de formule et est plus adaptée pour le raisonnement mécanisé. Les techniques de mise en forme clausale seront utiles pour faire des démonstrations par résolution ou pour les méthodes de décision de satisfiabilité. L’automatisation des preuves est le sujet du chapitre 4.



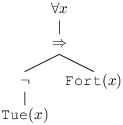
 Un litteral tout seul est une clause dans laquelle il n’y a pas de disjonction. En particulier
Un litteral tout seul est une clause dans laquelle il n’y a pas de disjonction. En particulier  Attention la remontée des quantificateurs au travers d’une négation change le quantificateur (loi de de Morgan) de même lorsqu’il est dans la partie gauche d’une implication. La remontée des quantificateurs se fait
Attention la remontée des quantificateurs au travers d’une négation change le quantificateur (loi de de Morgan) de même lorsqu’il est dans la partie gauche d’une implication. La remontée des quantificateurs se fait  la remontée naïve des quantificateurs peut engendrer une
la remontée naïve des quantificateurs peut engendrer une  La forme prénexe n’est pas unique. L’ordre des quantificateurs en particulier peut varier en fonction de l’ordre dans lequel on choisit de les faire remonter.
La forme prénexe n’est pas unique. L’ordre des quantificateurs en particulier peut varier en fonction de l’ordre dans lequel on choisit de les faire remonter. Dans beaucoup d’ouvrages, l’élimination du quantificateur existentiel se fait après avoir mis la formule en forme prénexe. On choisit alors l’arité du symbole de fonction introduit en fonction du nombre de quantifications universelles préalables. L’idée étant que si on a une alternance
Dans beaucoup d’ouvrages, l’élimination du quantificateur existentiel se fait après avoir mis la formule en forme prénexe. On choisit alors l’arité du symbole de fonction introduit en fonction du nombre de quantifications universelles préalables. L’idée étant que si on a une alternance  La skolémisation élimine les quantifications existentielles mais la formule obtenue
La skolémisation élimine les quantifications existentielles mais la formule obtenue  Les règles d’inférence pour faire des preuves reposent sur la syntaxe des formules, ainsi il n’est pas correct de transformer dans un séquent une formule par une autre formule équivalente (sauf si une règle nous autorise explicitement à le faire).
Les règles d’inférence pour faire des preuves reposent sur la syntaxe des formules, ainsi il n’est pas correct de transformer dans un séquent une formule par une autre formule équivalente (sauf si une règle nous autorise explicitement à le faire). Des présentations alternatives du calcul des séquents utilisent plutôt des multi-ensembles (des éléments peuvent apparaître plusieurs fois) à la fois dans les hypothèses et les conclusions. Cela nécessite d’introduire une règle explicite dite de
Des présentations alternatives du calcul des séquents utilisent plutôt des multi-ensembles (des éléments peuvent apparaître plusieurs fois) à la fois dans les hypothèses et les conclusions. Cela nécessite d’introduire une règle explicite dite de