Chapitre 4  Automatiser les démonstrations

• Peut-on automatiser les démonstrations ?
• Cas propositionnel
• Unification
• Résolution générale
• Calcul des séquents
• Théories décidables

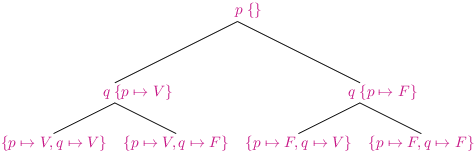
Dans ce chapitre nous introduisons plusieurs techniques pour automatiser les démonstrations en calcul propositionnel et logique du premier ordre.

4.1  Peut-on automatiser les démonstrations ?

Automatiser les démonstrations consiste à trouver un algorithme qui étant donnée une formule quelconque va pouvoir répondre à la question est-ce que cette formule est valide ?

On a vu que ce problème était équivalent à trouver un algorithme qui, pour une formule quelconque, répond à la question est-ce que cette formule est satisfiable ? En effet la validité de la formule A est équivalente à l’insatisfiabilité de la formule ¬ A.

4.1.1  Décidabilité de la logique propositionnelle

Preuve: Etant donnée une formule de la logique propositionnelle, elle a un nombre fini de variables, n. On peut calculer sa valeur de vérité pour chacune des 2ⁿ interprétations et en fonction du résultat, répondre à la question de la validité. □

Evidemment la méthode donnée ci-dessus n’est pas efficace et d’autres techniques existent pour rendre plus effective la procédure. On pourrait se dire que la question de la satisfiabilité d’une formule (problème SAT) est plus simple puisqu’il suffit de trouver une interprétation qui rend vraie la formule. Or ce n’est pas le cas, le problème reste intrinsèquement dur. On rappelle les définitions liées à la NP-complétude dans le cas du problème SAT :

• SAT est un problème NP : on peut construire une machine de Turing non-déterministe (à partir de chaque état, on peut choisir parmi un nombre fini de transitions possibles), chaque exécution est de taille polynomiale et le problème a une solution si et seulement si il existe un chemin d’exécution (au moins) qui réussit. Dans le cas du problème de la satisfiabilité d’un ensemble de formules, chaque étape peut faire un choix sur une variable (valeur vrai ou faux) et aboutir au calcul de la valeur de vérité des formules dans l’interprétation choisie. L’ensemble est satisfiable si et seulement si il y a au moins un chemin d’exécution qui donne la valeur vraie.
• SAT est NP-complet : tout problème NP est reductible de manière polynomiale à un problème SAT (codage propositionnel du problème).

Preuve: La preuve du fait que le problème de satisfiabilité est NP-complet va constituer à ramener la résolution du problème NP à une question de satisfiabilité en logique propositionnelle, en faisant un codage logique de la machine de Turing qui résoud le problème initial. □

On peut chercher des solutions plus efficaces pour des classes particulières de formules.

Si la formule est déjà en forme normale disjonctive, alors la satisfiabilité est immédiate car la formule est soit la formule ⊥ donc insatisfiable soit de la forme C∨ D avec C une conjonction élémentaire et cette conjonction élémentaire a un modèle qui est un modèle de la formule complète. La formule est donc satisfiable. Ce résultat associé au théorème de Cook implique que la complexité de la satisfiabilité se retrouve dans la complexité de mettre une formule quelconque en FND.

On a vu que l’on avait des méthodes linéaires pour ramener la satisfiabilité d’une formule à la satisfiabilité d’une formule en forme normale conjonctive. Cependant, même en se limitant à une formule en FNC dont les clauses propositionnelles ont au plus trois littéraux (problème dit 3-SAT), le problème SAT reste NP-complet.

4.1.2  Semi-décidabilité de la logique du premier ordre

Contrairement au cas propositionnel, dans le cas de la logique du premier ordre il y a une infinité d’interprétations possibles pour les symboles. On ne peut donc pas les énumérer toutes en général ou construire des tables de vérité.

Dans le cas des formules universelles (avec uniquement des quantificateurs universels en forme prénexe), le théorème de Herbrand nous permet de nous restreindre à une recherche parmi les modèles de Herbrand (interprétation sur le domaine des termes clos). Associé au théorème de compacité, il nous donne une méthode algorithmique pour savoir si une formule P (ou un ensemble de formules) est insatisfiable.

1. mettre la formule P en forme de Skolem ∀ x₁ … x_n,A avec A sans quantificateur. La formule P est satisfiable si et seulement si ∀ x₁ … x_n,A est satisfiable.
2. énumérer les instances closes de A : A₁,…,A_n,… (en remplaçant les variables x₁,…,x_n par des termes clos), et pour chaque préfixe A₁,…,A_p, utiliser une méthode propositionnelle pour tester la satisfiabilité :
   1. si A₁,…,A_p est insatisfiable alors ∀ x₁ … x_n,A est insatisfiable (en effet dans une interprétation où ∀ x₁ … x_n,A est vrai, a fortiori toutes les instances A₁,…,A_p sont aussi vraies).
   2. si A₁,…,A_p est satisfiable et s’il n’existe pas de nouvelle instance close (cas où le domaine de Herbrand est fini) alors ∀ x₁ … x_n,A est satisfiable car l’interprétation qui rend vraies toutes les formules de A₁,…,A_p définit un modèle de Herbrand dans lequel la formule ∀ x₁ … x_n,A est vraie.
   3. sinon on ajoute une nouvelle instance A_p+1 et on relance le problème

On peut établir les propriétés suivantes de l’algorithme :

• Si l’algorithme s’arrête alors la réponse donnée est correcte (simple application de la définition de la satisfiabilité) et on peut conclure que P est ou non satisfiable..
• Si la formule initiale est insatisfiable alors l’algorithme s’arrête et renvoie la bonne réponse (application du théorème de Herbrand et de la compacité).
• Si la formule initiale est satisfiable et le domaine de Herbrand infini, alors l’algorithme ne s’arrête pas. En effet il y a une infinité d’instances closes et tous les sous-ensembles seront satisfiables donc nécessiteront de relancer la recherche.

On en déduit les résultats suivants :

Preuve: Le premier résultat est une conséquence de l’algorithme présenté ci-dessus et le second en découle en utilisant le fait que tester la validité de A est équivalent à tester l’insatisfiabilité de la formule ¬ A. □

On peut s’interroger sur la possibilité de faire mieux, c’est-à-dire de décider de la validité d’une formule. La réponse est négative.

Preuve: La preuve se fait en ramenant un problème indécidable comme l’arrêt d’une machine de Turing ou la correspondance de Post à un problème de validité en logique du premier ordre. □

La preuve de semi-décidabilité nous a donné un algorithme naïf pour chercher une preuve d’une formule. En effet la méthode énumère au hasard l’ensemble des instances d’une formule et repose à chaque fois la question de la satisfiabilité. Pour améliorer cela, on peut chercher à engendrer des instances qui vont pouvoir interagir avec d’autres parties de la formule pour conduire à une contradiction.

4.2  Cas propositionnel

Dans cette section nous explorons plusieurs méthodes pour répondre à la question de la validité ou de la satisfiabilité d’une formule propositionnelle qui ne contient donc pour symboles que des variables propositionnelles et qui ne comporte pas de quantificateur.

4.2.1  Système G

Le système G est un calcul des séquents introduit au chapitre précédent (section 3.3.4).

Nous en rappelons les règles dans le cas propositionnel.

On a une règle “hypothèse” (Hyp)

et pour chaque connecteur, une règle gauche et une règle droite rappelées dans le tableau ci-dessous.

Ce système a de bonnes propriétés pour l’automatisation du raisonnement. En effet chaque séquent qui apparaît en prémisse d’une règle d’inférence contient moins de connecteurs logiques que celui qui est en conclusion et donc le processus qui consiste à appliquer les règles logiques s’arrête forcément.

On a vu aussi que toutes les règles étaient correctes et inversibles dans le sens qu’une interprétation rend vrai un séquent en conclusion d’une règle si et seulement si elle rend vrais tous les séquents qui apparaissent dans les prémisses.

En particulier, lorsqu’on construit un arbre de dérivation, si un nœud n’est pas valide, alors il existe une interprétation qui rend faux le séquent correspondant et on peut en déduire que la racine de la dérivation est également fausse pour cette interprétation. Et donc le séquent à la racine n’est pas valide. On en déduit une méthode de décision de la validité d’un séquent.

Preuve: Si les feuilles A₁,…,A_n ⊢ B₁,…,B_p ne contiennent plus de connecteurs logiques, les formules A₁,…,A_n,B₁,…,B_p sont des variables propositionnelles.

Si toutes les feuilles sont des instances de la règle “hypothèse”, l’arbre peut être complété et la conclusion est alors valide.

S’il existe une feuille de l’arbre A₁,…,A_n ⊢ B₁,…,B_p qui n’est pas une instance de la règle “hypothèse” alors elle ne contient que des variables propositionnelles distinctes. On peut donc construire une interprétation qui rend vraies les variables A_i et fausses toutes les variables B_j. Comme les règles sont inversibles, le nœud qui est le parent de cette feuille est également faux dans cette interprétation. Et donc la racine de l’arbre qui est le séquent qui nous intéresse est faux dans cette interprétation. Ce séquent n’est pas valide. □

Preuve: Le résultat découle de la propriété 1. On montre la contraposée à savoir que si le séquent n’est pas prouvable alors il n’est pas valide. En effet, en décomposant tous les connecteurs, on peut toujours construire un arbre dont les feuilles sont uniquement composées de variables propositionnelles. Une des feuilles de cet arbre n’est pas une instance de la règle hypothèse (sinon le séquent serait prouvable) et donc par le résultat précédent, le séquent A₁,…,A_n ⊢ B₁,…,B_p n’est pas valide. □

Exemple.

Soit la formule ⊢ A ∨ (B ∧ C) ⇒ (A ∨ B) ∧ C. Un arbre de dérivation partiel est  :

On voit qu’une des feuilles A ⊢ C n’est pas valide et donc on en déduit (sans finir la construction de l’arbre) que le séquent ⊢ A ∨ (B ∧ C) ⇒ (A ∨ B) ∧ C n’est pas prouvable non plus.

4.2.2  Résolution propositionnelle

Rappels.

Une clause est une disjonction de littéraux et peut se représenter par un ensemble de littéraux. Nous noterons une clause l₁∨…∨ l_n, chaque littéral apparaitra une seule fois et l’ordre est indifférent.

Le cas où cet ensemble est vide correspond à la proposition ⊥ qui est toujours fausse.

Si la clause contient la formule ⊤ ou contient une variable propositionnelle et sa négation, elle est toujours vraie (clause triviale). Nous nous intéressons à la satisfiabilité d’un ensemble de clauses, et une clause toujours vraie est satisfiable dans toutes les interprétations. Une clause triviale peut donc être retirée de l’ensemble considéré sans changer le problème (E est satisfiable si et seulement si E∪{⊤} est satisfiable). Une clause non triviale peut donc toujours se représenter par un ensemble de littéraux qui sont soit des variables propositionnelles soit des négations de variables propositionnelles et la même variable n’apparaît pas deux fois.

Règle de résolution.

On suppose donné un ensemble de clauses E. On cherche à savoir si ces clauses sont satisfiables, c’est-à-dire s’il existe une interprétation I telle que I⊨ E. La notation I⊨ E représente le fait que pour toute formule P∈ E, on a I⊨ P.

Pour cela on va se donner un système de règles qui nous permet de dériver de nouvelles clauses C telle que si I⊨ E alors on a aussi I⊨ C. Le but du jeu est d’aboutir à la clause vide qui représente ⊥ et qui est insatisfiable et donc d’en conclure que l’ensemble de clauses initial n’est pas satisfiable (il n’existe pas d’interprétation I telle que I⊨ E).

Preuve:

• Pour établir que E⊨ C, on se donne une interprétation I telle que I⊨ E et on établit que I⊨ C par minimalité de la définition de l’ensemble des clauses déductibles.
  • Si C∈ E alors c’est vrai.
  • Sinon, C est obtenue par résolution à partir de deux clauses C₁∨ p et C₂∨ ¬ p et on a alors C = C₁ ∨ C₂.

    La minimalité nous donne que I⊨ C₂∨ ¬ p et I⊨ C₁∨ p. On raisonne par cas suivant la valeur de la variable p dans l’interprétation I. Si p est vrai alors ¬ p est faux et donc I⊨ C₂ et si p est faux alors I⊨ C₁. Dans les deux cas, on a bien I⊨ C₁∨ C₂, c’est-à-dire I⊨ C.

  On en déduit que E⊨ C.
• Supposons qu’il existe une réfutation par résolution de E. Si E était satisfiable, d’après le résultat précédent on aurait une interprétation dans laquelle ⊥ est vrai, ce qui n’est pas possible. On en déduit que E est insatisfiable.
• Si on a une preuve par résolution de A à partir d’une ensemble de formule E alors on sait que la forme clausale de E ∪ {¬ A} est insatisfiable donc E ∪ {¬ A} est insatisfiable et donc E⊨ A.

□

Complétude

On peut se poser la question de savoir si la méthode de résolution peut toujours nous donner la solution. C’est-à-dire si on se donne un ensemble E de clauses insatisfiable, est-ce qu’il existe une réfutation de E par la méthode de résolution. La réponse est oui.

Preuve: On va faire la preuve dans le cas où d’un nombre fini ou dénombrable de variables propositionnelles (p_i)_i∈ℕ.

On construit un arbre binaire de décision. Chaque niveau est étiqueté par une variable propositionnelle, en partant de p₀, le sous-arbre gauche correspond au cas où cette variable vaut V et le sous-arbre droit, au cas où elle vaut F. Chaque branche (possiblement infinie) correspond donc à une interprétation logique des variables propositionnelles (p_i)_i∈ℕ.

Si on a juste deux variables p et q, l’arbre de décision se présentera ainsi (on a indiqué pour chaque sommet l’interprétation correspondante)

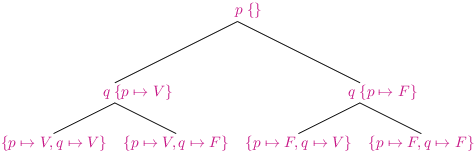
Chaque nœud interne de l’arbre correspond à une interprétation partielle des variables. Au niveau de la racine, aucune variable n’a de valeur.

Si l’ensemble E est insatisfiable alors pour chaque interprétation I, il existe une clause C∈E telle que I⊭C. Comme C n’a qu’un nombre fini de variables, on peut positionner la formule dans l’arbre le plus haut possible telle que l’interprétation I restreinte à p₀,…,p_n rend faux la clause C. Il est possible de faire cela pour toutes les branches de l’arbre. On va appeler un tel arbre un arbre de réfutation de E.

Par exemple un arbre de réfutation pour l’ensemble de clauses {p ∨ q , p ∨ ¬ q, ¬ p} est :

Un arbre à branchement fini dont toutes les branches sont finies est lui-même fini (lemme de König). Donc on a un arbre fini, et chaque feuille contient une clause de E qui est fausse dans l’interprétation correspondant à la branche. Soit un arbre de réfuytation pour un ensemble E de clauses insatisfiable. Il se peut que cet arbre soit réduit à une feuille, celle-ci doit correspondre à une formule qui est fausse dans l’interprétation vide, il ne peut s’agir que de ⊥ et donc ⊥∈ E et on a une réfutation triviale par résolution.

Si l’arbre n’est pas vide, on a un nœud de la forme avec p une variable propositionnelle et C et D des clauses. Soit I l’interprétation des variables autres que p qui correspond au chemin de la racine de l’arbre jusqu’à p. Attention I ne définit pas la valeur de toutes les variables propositionnelles, c’est seulement une interprétation partielle et donc toutes les clauses ne peuvent pas être évaluées dans cette interprétation.

On a I,{p↦ V}⊭C et I,{p↦ F}⊭D par définition des arbres de réfutation. La variable propositionnelle p apparait dans C et dans D (sinon on aurait pu faire remonter l’une de ces clauses plus haut dans l’arbre). On a forcément C=C′∨ ¬ p et D=D′∨ p (sinon les clauses seraient vraies à l’endroit où elles sont positionnées). Ce qui signifie que l’on peut faire une étape de résolution entre les deux clauses, qui nous donnera une clause C′∨ D′ telle que I ⊭C′∨ D′. On peut donc remplacer le sous arbre [.p C D ] par la clause C′∨ D′.

On voit donc qu’au fur et à mesure que l’on construit la déduction par résolution, on a un ensemble de clauses pour lequel l’arbre de réfutation diminue. Au final on aura un arbre réduit à une feuille ⊥ ce qui correspond à une réfutation. □

Evidemment cette démonstration n’est pas une manière effective de guider la recherche d’une réfutation par la méthode de résolution puisque si on avait l’arbre de réfutation on pourrait conclure immédiatement que l’ensemble de clauses est insatisfiable sans avoir recours à la résolution. Il faut parfois une peu d’intuition pour aboutir à la clause vide. Suivant la forme des clauses on peut avoir des stratégies plus précises.

Il se peut qu’en faisant une étape de résolution on trouve la clause triviale ⊤ ou que l’on retombe sur une clause déjà connue. Cela ne signifie pas forcément que l’on s’est trompé ou que l’ensemble de clauses est satisfiable mais juste que les étapes de calcul faites étaient inutiles. Il faut alors chercher d’autres combinaisons ou s’interroger si l’ensemble de clauses de départ est bien insatisfiable.

4.2.3  Satisfiabilité

Il existe des méthodes qui, au lieu de chercher une contradiction dans un ensemble de clauses, vont au contraire chercher à construire une interprétation qui satisfait l’ensemble des clauses en collectant les contraintes sur les variables induites par ces clauses.

La procédure DPLL (du nom de ses inventeurs Davis, Putnam, Logemann et Loveland) permet de dire si une formule en forme normale conjonctive (représentée par un ensemble de clauses) est satisfiable. Pour cela, l’algorithme cherche à construire une interprétation qui rend la formule vraie.
L’algorithme DPLL travaille sur des problèmes de la forme : I ≫ Δ avec I une interprétation partielle des variables propositionnelles de la forme {x₁↦ b₁;…;x_n↦ b_n} (que l’on peut aussi représenter comme un ensemble de littéraux x_i si b_i=V et ¬ x_i si b_i=F) et Δ un ensemble de clauses C₁,…,C_n. On note Δ,C le problème qui contient toutes les clauses de Δ plus la clause C. Le but de l’algorithme est de construire une interprétation qui étend I, c’est-à-dire de la forme {x₁↦ b₁;…;x_n↦ b_n;x_n+1↦ b_n+1… x_p↦ b_p} et qui rend vraies toutes les clause C_i.

Les règles sont les suivantes :

Il y a deux cas triviaux. Le premier cas s’il n’y a plus de clauses, l’interprétation I répond au problème. Le second cas si l’une des clauses C_i est la clause vide alors le problème n’a pas de solution. Cela correspond aux deux règles :

Par ailleurs on peut simplifier les problèmes : lorsque l’interprétation I fixe la valeur de la variable x, alors les clauses C qui contiennent un litteral l de la forme x ou ¬ x se simplifient :

• si I⊨ l alors la clause est trivialement vraie dans cette interprétation et peut être supprimée;
• si I⊭l alors on peut retirer le littéral l de la clause.

Ceci est représenté par les deux règles suivantes :

Maintenant si aucune des règles précédentes ne s’applique, alors il faut préciser l’interprétation en choisissant une valeur pour une nouvelle variable. Un cas simple est si une clause ne contient qu’un seul littéral alors pour que la clause soit vraie il faut choisir la valeur de la variable pour rendre ce littéral vrai. Ceci s’exprime par les règles suivantes :

Si maintenant, il n’y a aucune clause réduite à un littéral, alors il n’y a pas de choix évident. On va donc choisir une variable qui n’a pas encore de valeur et explorer les deux branches : celle où cette variable est interprétée par V et celle où elle est interprétée par F.

On part d’un ensemble de clauses Δ et d’une interprétation vide. On construit un arbre en utilisant les règles précédentes et on cherche à arriver à une feuille de succès de la forme I≫∅. L’interprétation I est une solution de notre problème, elle rend vraies l’ensemble des clauses Δ.

Si toutes les feuilles de l’arbre correspondent à des conflits alors l’ensemble de clauses initial n’est pas satisfiable.

4.3  Unification

On a vu que la question de la satisfiabilité nécessitait de produire des instances de formules, c’est-à-dire de remplacer des variables par des termes ayant de bonnes propriétés. Dans cette section, nous allons introduire un outil, l’unification, qui nous sera utile dans la méthode de résolution pour produire des instances particulières de formules. L’unification traite une classe de problèmes très simples à savoir des équations entre termes avec variables. C’est un problème qui a des applications multiples comme la question de l’inférence de types dans les langages fonctionnels.

L’unification est également l’ingrédient majeur des systèmes de réécritures qui sont des théories logiques dans lesquelles le seul symbole de prédicat est celui de l’égalité et les axiomes en plus de ceux de l’égalité sont de la ∀(t=u) de tels systèmes sont à la fois utilisés pour le raisonnement et comme langage de programmation.

4.3.1  Définitions

On se donne une signature F pour les termes et un ensemble X de variables. On rappelle qu’une substitution est une application σ ∈ X→ T(F,X). On s’intéresse à des substitutions dites à support fini c’est-à-dire telles que σ(x)=x sauf pour un nombre fini de variables. De telles substitutions se représentent facilement comme des ensembles finis {x← σ(x) | x∈ X ∧ σ(x)≠x}. Ainsi, la substitution identité telle que σ(x)=x pour tout x∈ X se représentera simplement par un ensemble vide {}.

Étant donnée une substitution, on a défini dans la section 1.5.3 une application de T(F,X)→ T(F,X) qui à un terme t associe le terme noté t[σ] dans lequel on a remplacé chaque variable x par σ(x).

D’un point de vue fonctionnel, la notation σ₁σ₂ correspond à appliquer la substitution σ₁ suivie de σ₂, ce qui d’un point de vue mathématiques correspond à la composition de fonctions σ₂∘σ₁

Remarque.

Il ne faut pas confondre la composition de deux substitutions qui correspond à deux substitutions successives avec la substitution simultanée. Ainsi si on pose σ₁={x← y} et σ₂={y← z}. On a σ₁σ₂={x← z;y← z} et (x+y)[σ₁σ₂]=z+z alors que la substitution simultanée est définie par {x← y;y← z} et donne le résultat (x+y)[x← y;y← z]=y+z.

Il s’agit de la résolution d’une équation (ou d’un système d’équations), on trouve des valeurs pour les variables qui apparaissent dans t et u, telles que si on remplace les variables par ces valeurs, alors les deux termes obtenus sont syntaxiquement égaux. On rappelle que les termes f(t₁,…,t_n) et g(u₁,…,u_p) sont (syntaxiquement) égaux uniquement lorsque les symboles f et g sont égaux, on a alors la même arité donc p=n et on doit avoir récursivement t_i=u_i pour i=1… n.

4.3.2  Ensemble des solutions

Si σ₁ est une solution du problème d’unification t=^? u alors il en est de même de σ₁σ₂ pour toute substitution σ₂. En effet on a t[σ₁]=u[σ₁] car σ₁ est solution du problème et donc t[σ₁σ₂]=t[σ₁][σ₂]=u[σ₁][σ₂]=u[σ₁σ₂].

Si on a deux solutions σ et τ a notre problème d’unification, on dira que σ est plus générale que τ s’il existe une substitution σ′ telle que σσ′=τ.

Une bonne propriété de l’unification sur les termes syntaxiques est que si un problème a une solution alors il existe une solution qui est plus générale que toutes les autres. Et donc pour calculer l’ensemble de toutes les solutions, il suffit de calculer cette substitution que l’on appelle aussi unificateur principal.

Proposition 1 (Unification, algorithme de Robinson)   Soit E={t_i=^? u_i|i ∈ I} un problème d’unification. Si ce problème admet une solution, alors il existe un unificateur principal σ et celui-ci est calculé par la fonction suivante :

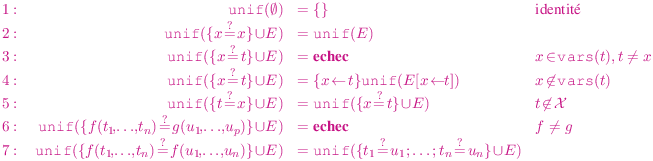
Preuve: On vérifie que chaque cas possible pour l’ensemble E est couvert par une équation unique : l’ensemble est soit vide soit il contient une équation et cette équation a son terme gauche qui est ou non une variable et si le terme gauche n’est pas une variable on regarde le cas où le terme droit est ou non une variable.

Un problème plus délicat à justifier est la terminaison de cette définition vue comme un procédé de calcul. Dans les cas récursifs, on regarde ce qui diminue :

• dans le cas (2) le nombre de problèmes diminue mais par ailleurs il augmente dans le cas (7);
• dans le cas (7) ce qui diminue c’est la taille globale du problème (nombre de symboles) car on a fait disparaître deux occurrences de f, mais la taille du problème augmente par ailleurs dans le cas (4) lorsque l’on remplace la variable x par t;
• dans le cas (4), la taille du problème grossit mais on a fait disparaitre une variable (x).

En résumé pour un problème E si on regarde le triplet nbvars(E),taille(E),nbeqs(E) avec nbvars(E) le nombre de variables différentes dans E, taille(E) le nombre d’occurrences de symboles dans E, et nbeqs(E) le nombre d’équations dans E, alors on remarque que chaque appel se fait sur un problème strictement plus petit si on prend l’ordre lexicographique, sauf celui où on change l’équation t=x en x=t. Mais cette règle n’est appliquée que lorsque t n’est pas une variable et sera donc immédiatement suivie de l’application d’une règle qui fait diminuer le “poids” du problème. Une autre possibilité est de définir taille(t=^? u) =^def  2× nbsymb(t)+nbsymb(u) au lieu de taille(t=^? u) =^def  nbsymb(t)+nbsymb(u). On a alors taille(x=^? t)<taille(t =^? x) lorsque t n’est pas une variable.

On vérifie que les cas d’échec correspondent à des problèmes sans solution et que dans les cas où une solution est trouvée, il s’agit bien de l’unificateur principal. □

L’algorithme de Robinson est naturel mais n’est pas efficace à cause en particulier de l’opération de substitution lorsqu’on élimine l’équation x=^? t. On peut utiliser une représentation des termes qui rend cette opération moins coûteuse. Il existe d’autres algorithmes plus complexes mais plus efficaces.

Autres applications de l’unification.

L’unification est une opération utilisée dans de nombreuses applications, par exemple dans l’algorithme de typage des programmes Ocaml afin de trouver le type le plus général que peut traiter une fonction. L’unification se généralise également à des théories plus complexes dans lesquelles l’égalité entre termes n’est plus syntaxique mais prend en compte des propriétés des opérations comme la commutativité ou l’associativité. Suivant les théories, on va perdre la décidabilité ou l’existence d’un unificateur principal.

Unification de littéraux.

L’unification sur les termes se généralise en une unification entre des littéraux. Si on a deux littéraux P et Q, ils s’unifient s’il existe une substitution σ telle que P[σ]=Q[σ]. Si P est de la forme R(t₁,…,t_n) (resp. ¬ R(t₁,…,t_n)) alors σ est un unificateur de P et Q si et seulement si Q est de la forme R(u₁,…,u_n) (resp. ¬ R(u₁,…,u_n)) et σ est un unificateur de l’ensemble de problèmes {t_i=^? u_i|i=1… n}.

4.3.3  Ordre sur les termes et filtrage

Preuve: Si t≤ u alors u=t[σ] et toute instance close de u est de la forme u[τ]=t[σ][τ]=t[στ] et est donc une instance close de t. □

Le langage Ocaml permet de définir une expression par cas suivant un ensemble de motifs

A l’exécution, e a pour valeur un terme clos (v)

• la première branche dont le motif p correspond (ie. p[σ]=v ou encore v∈inst(p)) est exécutée
• on donne aux variables du motif les valeurs de la substitution σ

On peut analyser les motifs

• Est-il possible de changer l’ordre des motifs, de les exécuter en parallèle ?
• Tous les cas sont-ils couverts ?
• Certains cas sont-ils inutiles ?

4.4  Résolution générale

On s’intéresse ici au problème de savoir si un ensemble de formules de la logique du premier ordre est satisfiable ou non, c’est-à-dire s’il existe une interprétation qui rend vraies simultanément toutes les formules. On rappelle qu’un ensemble fini de formules est satisfiable si et seulement si la conjonction de toutes les formules est elle-même une formule satisfiable. On a vu au chapitre 3 que l’on pouvait se ramener au cas où les formules manipulées sont uniquement des clauses (disjonction de littéraux), universellement quantifiées dans le cas de la logique du premier ordre.

La technique de preuve par résolution est importante car elle est à la base non seulement de systèmes de démonstration automatique mais aussi de systèmes de programmation logique. Le plus connu est le langage de programmation Prolog, dans lequel le programme est modélisé comme un ensemble de clauses et un calcul se fait par la recherche d’une preuve.

Nous avons traité le cas de la résolution en logique propositionnelle, nous voyons ici comment la méthode se généralise en logique du premier ordre.

4.4.1  Résolution au premier ordre

En logique propositionnelle, une clause est un ensemble de littéraux (variable propositionnelle ou négation de variable propositionnelle) et on se ramène au cas où chaque variable propositionnelle apparaît une seule fois.

Dans le cas du premier ordre, les littéraux sont de la forme R(t₁,…,t_n) ou ¬ R(t₁,…,t_n) avec R un symble de prédicat et t_i des termes. Le même symboles peut donc apparaître plusieurs fois dans la clause de manière positive ou négative associée à des termes différents.

Par ailleurs les termes qui apparaissent dans les clauses peuvent contenir des variables. De fait une clause C qui contient les variables {x₁,…,x_n} est juste une représentation sans quantificateur de la formule ∀ (C) (notation pour ∀ x₁ … x_n,C).

Une autre interprétation de la clause avec variables C est l’ensemble des instances closes (sans variable) de la formule c’est-à-dire l’ensemble des clauses C[σ₀] avec σ₀ une substitution qui remplace chaque variable de C par un terme clos. Le théorème de Herbrand nous a permis d’établir que la satisfiabilite de la formule ∀ (C) était équivalente à la satisfiabilité de l’ensemble (potentiellement infini) de toutes les instances closes de C. C’est ce qui est exploité dans la résolution au premier ordre.

On part d’un ensemble de clauses (disjonction de littéraux vue comme un ensemble de littéraux). On rappelle que l’unification sur les termes s’étend de manière naturelle à l’unification sur les littéraux. Deux littéraux L₁ et L₂ s’unifient s’ils sont de la forme R(t₁,…,t_n) et R(u₁,…,u_n) ou bien ¬ R(t₁,…,t_n) et ¬ R(u₁,…,u_n) et que le problème (t_i=^? u_i)_{i=1… n} admet une solution. Dans ce cas on note unif(L₁,L₂) l’unificateur principal.

Règles pour la résolution

Les définitions de réfutation par résolution et de preuve par résolution sont les mêmes que dans le cas propositionnel (définition 2) mais avec la notion de déduction par résolution générale.

La règle de renommage sert juste à préparer les clauses pour appliquer la règle de résolution dont une des conditions est que les deux clauses ne partagent pas de variable.

La règle de factorisation permet de faire disparaitre plusieurs littéraux lors d’une étape de résolution binaire. Elle est indispensable comme l’illustre l’exemple ci-dessous.

Ces deux règles sont triviales dans le cas propositionnel. La règle de résolution générale généralise la règle de résolution propositionnelle.

Propriétés de la résolution

La correction de la méthode de résolution établit que si l’on peut déduire une clause C à partir d’un ensemble de clauses E alors la formule ∀(C) est conséquence logique de l’ensemble des formules {∀ (D)|D ∈ E}.

On commence par établir quelques propriétés simples qui relient entre elles les clauses généralisées et leurs instances. Soient A et B deux formules, x une variable et t un terme.

• (∀ x,A)⊨ A[x← t]
• Si A⊨ B alors (∀ x,A)⊨ B
• Si A⊨ B et x∉Vl(A) alors A⊨ ∀ x,B

Ces résultats se généralisent au cas de plusieurs formules et plusieurs variables. Si σ est une substitution alors ∀ (C) ⊨ C[σ] qui se déduit du lien entre substitution et vérité :

Par ailleurs si E est un ensemble de formules, si E ⊨ B et si les variables libres de B ne sont pas libres dans les formules de E, alors E ⊨ ∀ (B).

Preuve: On va montrer la correction de chacune des règles en montrant que la généralisation de la conclusion (clause sous la barre) est une conséquence logique de la généralisation des hypothèses (clause(s) au-dessus de la barre):

1. Factorisation. Soit σ l’unificateur principal de L₁ et L₂, la règle de factorisation s’écrit 

   L1 ∨ L2 ∨ C L1[σ]∨ C[σ]

   On veut montrer ∀ (L₁ ∨ L₂ ∨ C) ⊨ ∀ (L₁[σ]∨ C[σ]).
   On a ∀ (L₁ ∨ L₂ ∨ C) ⊨ L₁[σ]∨ L₂[σ]∨ C[σ] mais comme L₁[σ]=L₂[σ] (propriété de l’unificateur), on peut simplifier et on obtient ∀ (L₁ ∨ L₂ ∨ C) ⊨ L₁[σ]∨ C[σ] puis ∀ (L₁ ∨ L₂ ∨ C) ⊨ ∀ (L₁[σ]∨ C[σ]) car ∀ (L₁ ∨ L₂ ∨ C) ne contient pas de variable libre.
2. Renommage. Si σ est une bijection sur les variables, la règle de renommage s’écrit

   C

   C[σ]

   .
   On a ∀ (C)≡∀ (C[σ]) (il s’agit d’une simple permutation des quantificateurs universels) d’où le résultat ∀ (C)⊨∀ (C[σ]) .
3. Résolution binaire. Si σ est l’unificateur principal de L₁ et L₂, la règle de résolution s’écrit

   L1 ∨ C      ¬ L2 ∨ C′ C[σ]∨ C′[σ]

   On veut montrer ∀(L₁ ∨ C),∀(¬ L₂ ∨ C′)⊨ ∀(C[σ]∨ C′[σ]).
   On a ∀(L₁ ∨ C) ⊨ L₁[σ]∨ C[σ] et ∀(¬ L₂ ∨ C′) ⊨ ¬ L₂[σ]∨ C′[σ].
   On a L₁[σ]=L₂[σ] (propriété de l’unificateur) donc le même raisonnement que dans le cas propositionnel nous donne que L₁[σ]∨ C[σ],¬ L₂[σ]∨ C′[σ]⊨ C[σ]∨ C′[σ].
   Et donc ∀(L₁ ∨ C),∀(¬ L₂ ∨ C′)⊨ C[σ]∨ C′[σ] et finalement ∀(L₁ ∨ C),∀(¬ L₂ ∨ C′)⊨ ∀ (C[σ]∨ C′[σ]) car les variables libres de C[σ]∨ C′[σ] ne sont pas libres dans ∀(L₁ ∨ C),∀(¬ L₂ ∨ C′).

□

La méthode de résolution est aussi complète dans le cas de la logique du premier ordre, c’est-à-dire que si E est un ensemble de clauses et que ⊥ est une conséquence logique de {∀(C)|C ∈ E} alors on peut déduire la clause vide par la méthode de résolution à partir de l’ensemble E.

Ce résultat utilise le Théorème de Herbrand et la compacité qui nous permettent d’établir qu’il existe un ensemble fini insatisfiable d’instances closes des clauses de E :

.

L’ensemble F est propositionnel, on peut donc par le théorème de complétude de la résolution propositionelle construire une réfutation par résolution de cet ensemble.

La clé de la preuve est ensuite le Lemme de relèvement qui permet d’établir que les étapes faites au niveau de la déduction propositionnelle peuvent se simuler au travers des règles de résolution au premier ordre.

Nous ne détaillerons pas la preuve ici. On pourra regarder plus précisément les points suivants.

1. pourquoi peut-on utiliser la même substitution pour C et D?
2. à quoi sert la règle de factorisation ? de renommage ?

4.4.2  Questions de stratégie

La méthode de résolution consiste à combiner des clauses dans le but d’obtenir la clause vide. Néanmoins il y a de nombreuses manières différentes de la faire et on peut s’interroger s’il existe des stratégies plus efficaces que d’autres.

Eliminer les clauses inutiles

Supposons qu’un des symboles de prédicat R n’apparaisse que de manière positive dans les clauses. Alors toutes les clauses dans lesquelles ce symbole apparaît peuvent être éliminées.

Le même résultat s’applique si le symbole R n’apparait que de manière négative dans les clauses.

Il arrive que dans une dérivation, on puisse retomber sur une clause qui ressemble à une clause déjà rencontrée. Supposons qu’on ait à la fois une clause C et une clause C[σ]∨ D, alors la clause C[σ]∨ D peut être ignorée. En effet on a ∀(C)⊨ ∀ (C[σ]∨ D) donc E,∀(C),∀ (C[σ]∨ D)⊨ ⊥ si et seulement si E,∀(C)⊨ ⊥

Stratégie unitaire et clauses de Horn

Lorsque l’on combine deux clauses par la méthode de résolution, on peut obtenir en général une clause qui est aussi grosse voir plus grosse que les clauses dont on est parti. Sauf si une des deux clauses est composée d’un seul litteral (on dit que la clause est unitaire) auquel cas la clause obtenue après résolution est plus petite que la clause dont on était parti.

Malheureusement, la stratégie de choisir de faire toujours une résolution avec une clause réduite à un littéral ne fonctionne pas. En effet il y a des ensembles de clauses contradicatoires qui ne contiennent pas de clause unitaire et la stratégie de choisir toujours une clause unitaire peut nous amener à ne jamais considérer ces clauses. C’est ce qui se passe dans l’exemple suivant :

La stratégie unitaire engendre un ensemble infini de clauses {P(f(a)),P(f(f(a))),…,P(fⁿ(a)),…} qui ne mêne pas à une contradiction alors que l’ensemble {¬ p ∨ ¬ q,¬ p ∨ q, p ∨ ¬ q,p∨ q} est lui insatisfiable (comme montré dans l’exercice 3).

Les clauses de Horn sont des cas particuliers de clauses qui contiennent au plus un seul littéral positif (sans négation). Les règles de la résolution appliquées à des clauses de Horn produisent des clauses de Horn.

L’intérêt des clauses de Horn réside dans le résultat suivant.

Preuve: La preuve suit les étapes suivantes

• Si toutes les clauses ont un littéral négatif alors l’ensemble est satisfiable. En effet il suffit alors de choisir une interprétation dans laquelle tous les symboles de prédicats sont interprétés comme l’ensemble vide. Toutes les clauses auront alors leur littéral négatif qui vaut vrai et seront donc vraies.
• Si l’ensemble est insatisfiable alors il existe une clause sans littéral négatif donc avec un seul littéral positif puisque ce sont des clauses de Horn.
• Toute dérivation de la clause vide contient au moins une étape de résolution unitaire, puisqu’elle doit impliquer une des clauses sans littéral négatif.
• On peut transformer les étapes de résolution pour faire “remonter” les résolutions unitaires en utilisant la transformation suivante (présentée dans le cas propositionnel) :

  ¬ A ∨ C ∨ l          C′ ∨ ¬l ¬ A ∨ C∨ C′           A C∨ C′

  ¬ A ∨ C ∨ l          A C ∨ l           C′ ∨ ¬l C∨ C′

• En itérant cette opération on peut construire une dérivation dont toutes les étapes de résolution sont unitaires.

□

Application à la programmation logique

En 1972, l’informaticien Alain Colmerauer qui s’intéressait au traitement automatique des langues introduit, avec Philippe Roussel, le langage ProLog.

Le principe de base est de modéliser un problème à l’aide de Clauses de Horn.

Une clause avec un littéral positif p : ¬ p₁∨ … ∨ ¬ p_n∨ p est écrite sous la forme p:- p₁,…, p_n. et peut se lire comme (p₁∧ … ∧ p_n) ⇒ p qui est bien équivalent à ¬ p₁∨ … ∨ ¬ p_n∨ p

Lorsque la clause ne contient pas de littéral positif, elle s’écrira sous la forme :- p₁,…, p_n. et peut se lire comme (p₁∧ … ∧ p_n) ⇒ ⊥ qui est bien équivalent à ¬ p₁∨ … ∨ ¬ p_n ≡ ¬(p₁∧ … ∧ p_n).

Lorsque la clause est composée uniquement d’un littéral positif p, elle s’écrit simplement p.

Pour exécuter un programme, on va poser des questions sous la forme d’une conjonction de littéraux positifs qui peuvent contenir des variables.

Le système va rechercher les instances de ce programme qui sont conséquence logique des clauses du programme. Pour cela il va utiliser la méthode de résolution pour rechercher des contradictions à partir de la négation de ces prédicats.