Eléments de logique pour l’informatique 2020–21 http://www.lri.fr/~paulin/Logique
Annexe A Correction des exercices
A.1 Exercices du chapitre 1
Exercice 1
-
∀ x y, ami(self,x)∧ ami(x,y)⇒ ami(self,y)
- ∀ x, joue(self,x)⇒ ami(self,x)
- ¬ ∃ x, joue(self,x) ∧ ami(self,x) ou de manière équivalente
∀ x, ¬ joue(self,x) ∨ ¬ ami(self,x)
- ∃ x y, joue(self,x) ∧ joue(self,y)∧ ¬(x=y) sans la mention de x≠y la formule est vraie dès qu’il existe une personne avec qui je joue.
- ∀ x, ∃ y, ami(x,y)
Exercice 2
∀ x y, pair(x)∧ pair(y)⇒ pair(x+y)
Exercice 3
-
∀ x∈ℕ,P correspond à ∀ x,N(x)⇒ P
- ∃ x∈ℕ,P correspond à ∃ x,N(x)∧ P
Exercice 4
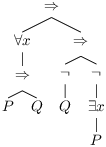
La formule parenthésée est (∀ x, (P ⇒ Q)) ⇒ ((¬ Q) ⇒ (¬ (∃ x, P))) et sous forme d’arbre :
Exercice 5
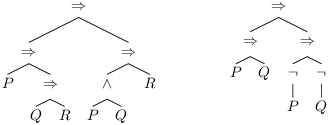
Les formules parenthésées sont (P ⇒ (Q ⇒ R)) ⇒ ((P ∧ Q) ⇒ R) et
(P ⇒ Q) ⇒ ((¬ Q) ⇒ (¬ P))
et sous forme d’arbre
Exercice 6
-
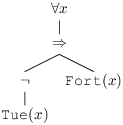
∀ x, ¬ Tue(x) ⇒ Fort(x) correspond au minimum de parenthèses
- ∀ x, ((¬ Tue(x)) ⇒ Fort(x)) formule complètement parenthésée
- Forme arborescente
Exercice 7
La seule variable libre de la formule : ∀ b, b > 0 ⇒
∃ q, ∃ r, a = b × q + r ∧ r < b est a.
Exercice 8
-
La formule ((P ⇒ Q) ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors P ⇒ Q est vrai et donc (P ⇒ Q) ⇒ P est faux et donc ((P ⇒ Q) ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
- La formule (¬ P ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors ¬ P est vrai et donc ¬ P ⇒ P est faux et donc (¬ P ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
Exercice 9
-
L’inscription sur la porte 1 correspond à la formule A1 =def P1 ∧ ¬ P2,
- L’inscription sur la porte 2 correspond à la formule A2≡ (P1 ∧ ¬ P2)∨ (P2 ∧ ¬ P1),
- Une seule de ces inscriptions est vraie donc la formule (A1∧ ¬ A2) ∨ (A2∧ ¬ A1) est vraie.
On peut faire une table de vérité de cette dernière formule en fonction des valeurs de P1 et P2 et chercher dans quels cas elle est vraie.
On peut aussi raisonner directement.
Comme A2 est de la forme A1 ∨ B, si A1 est vrai alors A2 est vrai et donc la troisième formule est fausse.
Donc A1 est faux et A2 est vrai et on a P2 ∧ ¬ P1 donc il faut ouvrir la deuxième porte.
Exercice 10
La formule (∀ x, P(x)) ⇒ ∃ x, P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ∀ x, P(x). L’interprétation de P est vraie pour toutes les valeurs dans le domaine D. Comme le domaine est non vide, on peut choisir d∈ D. L’interprétation de P est vraie pour d et donc ∃ x, P(x) est vraie dans cette interprétation.
La formule ¬(∀ x, P(x)) ⇒ ∃ x, ¬ P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ¬(∀ x, P(x)). Cette interprétation rend faux ∀ x, P(x) ce qui veut dire qu’il existe d∈ D pour lequel l’interprétation P est fausse et donc l’interprétation de ∃ x, ¬ P(x) est vraie.
Exercice 11
t ≤ u =def ∃ n,
n+t=u.
-
∀ x, 0 ≤ x se réécrit en ∀ x, ∃ n, n+0=x. Soit x quelconque, on choisit pour n la valeur x. Il faut alors montrer x+0=x qui est l’axiome 4 de la théorie arithmétique.
- ∀ x y, x ≤ y ⇔ S(x) ≤ S(y) se réécrit en
∀ x y, (∃ n, n+x=y) ⇔ (∃ n, n+S(x)=S(y)). Soit x et y quelconques, on montre les deux côtés de l’équivalence.
Si ∃ n, n+x=y, soit n tel que n+x=y, on a S(n+x)=S(y) (propriété de la théorie de l’égalité). On en déduit n+x=y (axiome 5 de l’arithmétique) et donc ∃ n, n+S(x)=S(y).
Réciproquement si ∃ n, n+S(x)=S(y), soit n tel que n+S(x)=S(y), on en déduit S(n+x)=S(y) (axiome 5 de l’arithmétique). On en déduit n+S(x)=S(y) (axiome 3 de l’arithmétique) et donc ∃ n, n+x=y.
choisit pour n la valeur x. Il faut alors montrer x+0=x qui est un axiome de la théorie arithmétique.
- transitivité : ∀ x y z, x ≤ y ⇒ y ≤ z ⇒
x ≤ z se réécrit en (∃ n, n+x=y)⇒ (∃ m, m+y=z) ⇒ (∃ p, p+x=z).
Soit x,y et z quelconques, on suppose ∃ n, n+x=y et ∃ m, m+y=z vrai et donc soit n et m tels que n+x=y et m+y=z. Par la théorie de l’égalité, on a m+(n+x)=m+y et par la transitivité de l’égalité on en déduit m+(n+x)=z. L’associativité de l’addition (non démontrée) permet d’en déduire que (m+n)+x=z
et donc ∃ p, p+x=z ce qui conclut la preuve.
Exercice 12
Il est nécessaire en plus du prédicat pos(i,j,k) qui exprime que le chiffre k est sur la case (i,j) de disposer du prédicat d’égalité pour pouvoir dire qu’un chiffre apparait au plus une fois.
-
Un seul chiffre k par case (i,j): ∀ i j k, pos(i,j,k) ⇒ ∀ l, ¬ l=k⇒ ¬ pos(i,j,l)
- Chaque chiffre k apparaît sur chaque ligne i au moins dans une colonne j:
∀ i k, ∃ j, pos(i,j,k)
- Chaque chiffre k apparaît au plus une fois sur chaque ligne i (s’il est dans la colonne j, il n’est pas dans une autre colonne) :
∀ i j1 j2 k, pos(i,j1,k)∧ pos(i,j2,k)⇒ j1=j2
- Le cas des colonnes est analogue à celui des lignes. On traite ici la notion de carré. Si on veut éviter de traiter chaque valeur de ligne et de colonne individuellement, on peut introduire un symbole de fonction tiers unaire qui, étant donné une ligne ou une colonne, va nous dire dans quel tiers du tableau elle se trouve (premier, deuxième ou troisième). On peut ainsi tester si deux positions (i1,j1) et(i2,j2) seront dans le même carré si et seulement si les indices de ligne sont dans le même tiers du tableau et de même pour les indices de colonnes.
Pour représenter le fait que chaque chiffre k apparaît au plus une fois dans chaque carré on utilisera la formule :
| ∀ i1 i2 j1 j2 k, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2) |
| ⇒ pos(i1,j1,k)∧ pos(i2,j2,k) |
| ⇒ i1=i2∧ j1=j2 |
|
On peut aussi représenter le fait que chaque chiffre apparaitra au moins une fois dans chaque carré de la manière suivante :
| ∀ i1 j1 k, ∃ i2 j2, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2)∧ pos(i2,j2,k) |
Les deux formules sont redondantes dès lors qu’il y a 9 valeurs et 9 cases puisqu’on a écrit qu’il y avait au moins une valeur par case et qu’il ne pouvait pas y avoir deux fois la même valeur, donc chaque valeur va apparaître au moins une fois (une application injective (resp. surjective) d’un ensemble fini dans un ensemble de même cardinal est bijective.
- reste à exprimer dans la logique le fait qu’on a 9 valeurs possibles pour les lignes, les colonnes et les chiffres dans les cases. Cela se fait en ajoutant 9 constantes :1,…,9. AInsi qu’un axiome qui dot que l’univers est formé uniquement de ces 9 éléments
∀ x,x=1∨ …∨ x=9 auquel il faut ajouter les 36 axiomes qui disent que les constantes sont différentes deux à deux ¬1=2,¬1=3,…,¬1=9,¬2=3,…, ¬8=9.
Il faudra aussi ajouter les 9 axiomes qui permettent de raisonner sur la fonction tiers à savoir
tiers(1)=1,tiers(2)=1,tiers(3)=1,…,,tiers(9)=3.
Exercice 13
| nbsymb(p) | =0 si p atomique |
| nbsymb(¬ A) | =1+ nbsymb(A) |
| nbsymb(∀ x, A) | = 1+nbsymb(A) |
| nbsymb(∃ x, A) | = 1+nbsymb(A) |
| |
|
| | nbsymb(A∧ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A∨ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A⇒ B) | =1+ nbsymb(A)+nbsymb(B) |
|
Exercice 14
| prof(p) | =0 si p atomique |
| prof(¬ A) | =1+ prof(A) |
| prof(∀ x, A) | = 1+prof(A) |
| prof(∃ x, A) | = 1+prof(A) |
| |
|
| | prof(A∧ B) | =1+ max(prof(A),prof(B)) |
| prof(A∨ B) | =1+ max(prof(A),prof(B)) |
| prof(A⇒ B) | =1+ max(prof(A),prof(B)) |
|
Exercice 15
-
si x ∈ X alors vars(x)={x}
- si c ∈ F0 alors vars(c)=∅
- si f ∈ Fn alors vars(f(t1,…,tn))=
vars(t1)∪…∪ vars(tn)
Exercice 16
On considère ici des termes qui ne contiennent pas de variable
-
définition de feuilles
| feuilles(є)=1 feuilles(N(l,r)) = feuilles(l)+feuilles(r) |
- définition de noeuds
| noeuds(є)=0 noeuds(N(l,r)) = 1+noeuds(l)+noeuds(r) |
- preuve par récurrence que pour tout terme t sans variable, on a feuilles(t)=noeuds(t)+1.
-
cas où t est la constante є on a
feuilles(є)=1 et noeuds(є)=0 d’où le résultat.
- cas où t est de la forme N(l,r) avec l et r deux sous-arbres qui vérifient l’hypothèse de récurrence
feuilles(l)=noeuds(l)+1 et feuilles(r)=noeuds(r)+1.
On a
| feuilles(N(l,r)) | = feuilles(l)+feuilles(r) | définition de feuilles |
| | =noeuds(l)+1+noeuds(r)+1 | hypothèses de récurrence |
| | =noeuds(N(l,r))+1 | définition de noeuds |
|
On en déduit que la propriété est vraie pour tous les arbres.
Exercice 17
La théorie de l’égalité contient les axiomes pour la reflexivité, la symétrie et la transitivité ainsi que des axiomes pour les symboles de fonctions et les prédicats d’arité au moins 1.
Dans le cas de la signature qui est donnée, il y aura donc deux axiomes
-
∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ g(x1,y1)=g(x2,y2)
- ∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ Q(x1,y1)⇒ Q(x2,y2)
On veut montrer que la formule t=u ⇒ v[x← t]=v[x← u] est valide :
On se place dans une interprétation qui rend vraie la formule t=u (et les axiomes de l’égalité).
On commence par montrer par récurrence sur la structure du terme v que la formule
v[x← t]=v[x← u] est également vraie.
-
si v est une variable z alors soit z=x et la formule devient t=u qui est vraie par hypothèse sur l’interprétation, soit z≠x et la formule devient z=z qui est vraie par reflexivité de l’égalité.
- si v est la constante a alors la formule devient a=a qui est vraie par reflexivité de l’égalité.
- si v est de la forme g(v1,v2) avec v1 et v2 qui vérifient l’hypothése de récurrence à savoir v1[x← t]=v1[x← u] et v2[x← t]=v2[x← u]. On a g(v1,v2)[x← t]=g(v1[x← t],v2[x← t]), par définition de la substitution. En appliquant les hypothèses de récurrence et l’axiome 1 de l’égalité ci-dessus, on obtient g(v1,v2)[x← t]=g(v1[x← u],v2[x← u]) et donc finalement
g(v1,v2)[x← t]= g(v1,v2)[x← u]
On montre ensuite par récurrence sur la formule P que pour tous les termes t et u et toute interprétation qui rend vraie t=u, on a P[x← t]⇒ P[x← u] est vraie quelque soit l’environnement pour les valeurs des variables libres de P[x← t].
-
Si P est une formule atomique alors si c’est ⊥ ou ⊤ qui ne contient pas x alors il faut montrer P⇒ P qui est une tautologie.
Si P est de la forme Q(v1,v2) alors il faut montrer
Q(v1,v2)[x← t]⇒ Q(v1,v2)[x← u]
Par definition de la substitution, cela revient à montrer
Q(v1[x← t],v2[x← t])⇒ Q(v1[x← u],v2[x← u])
en utilisant l’axiome 2 de la théorie de l’égalité, il suffit de montrer
v1[x← t]=v1[x← u]∧ v2[x← t]=v2[x← u]. Or cette propriété est vraie d’après ce que nous avons établi précédemment.
- Si P est de la forme ¬ A alors il faut montrer (¬ A)[x← t]⇒ (¬ A)[x← u], c’est-à-dire ¬ (A[x← t])⇒ ¬ (A[x← u]) en prenant la contraposée, on est ramené à montrer A[x← u]⇒ A[x← t]. Comme une interprétation qui rend vraie t=u rend aussi vraie u=t par symétrie de l’égalité, on peut appliquer l’hypothèse de récurrence à A avec les termes u et t.
- Si P est de la forme A∘ B avec circ l’un des 2 connecteurs propositionnels ∧ ou ∨, alors il faut (A∘ B)[x← t]⇒ ((A∘ B)[x← u], c’est-à-dire (A[x← t]∘ B[x← t])⇒ (A[x← u]∘ B[x← u]) or par hypothèse de récurrence on A[x← t]⇒ A[x← u] et B[x← t]⇒ B[x← u]. On conclut en utilisant les propriétés des connecteurs (si A1⇒ A2 et B1⇒ B2 alors A1∧ B1⇒ A2∧ B2 et A1∨ B1⇒ A2∨ B2.
- Si P est de la forme A⇒ B, le raisonnement est presque le même sauf que
la propriéte (A1⇒ B1)⇒ (A2⇒ B2) est une conséquence de A2⇒ A1 et B1⇒ B2. Il faut donc intervertir t et u comme dans le cas de la négation.
- So P est de la forme ∀ z,A. On choisit la variable liée z pour qu’elle ne soit pas libre ni dans t ni dans u (sinon la substitution n’est pas définie) et qu’elle soit différente de x (sinon (∀ x,A)[x]v=(∀ x,A) et la propriété est trivialement vraie.
On doit montrer (∀ z,A)[x← t]⇒ ((∀ z,A)[x← u], c’est-à-dire
(∀ z,(A[x← t])⇒ (∀ z,(A[x← u])
Par hypothèse de récurrence on sait que (A[x← t])⇒ (A[x← u])
quelle que soit la valeur que l’on donne pour z dans l’environnement.
On en déduit que (∀ z,(A[x← t]))⇒ (A[x← u]) est vraie pour toute valeur possible de z. En effet si on prend une valeur pour z et que ∀ z,(A[x← t]) est vrai alors A[x← t] est a fortiori vrai pour cette valeur de z et donc A[x← u].
De (∀ z,(A[x← t]))⇒ (A[x← u]) vrai pour toutes les valeurs de z, on déduit que (∀ z,(A[x← t]))⇒ ∀ z,(A[x← u]) est vrai.
On peut de manière analogue déduire de (A[x← t])⇒ (A[x← u]) vrai
pour toutes valeur de z que (∃ z,(A[x← t]))⇒ ∃ z,(A[x← u]) est vrai. En effet si ∃ z,(A[x← t]) alors il existe une valeur v0 telle que A[x← t] pour cette valeur de z, donc A[x← u] est vraie pour cette même valeur de z et donc ∃ z,A[x← u] est vraie.
Exercice 1
| | ℕ | ℤ | ℚ |
| ∀ x, ∃ y, x < y | V | V | V |
| ∀ x, ∃ y, y < x | F | V | V |
| ∀ x y, x < y ⇒ x+1 ≤ y | V | V | F |
| ∀ x y z, x ≤ y ⇒ x× z ≤ y × z | V | F | F |
|
Exercice 2
-
(∃ x,¬ P(x)) ⇒ ¬ ∀ x,P(x) est valide (on peut s’appuyer sur la loi de de Morgan qui dit que ¬ ∀ x,P(x) ≡ ∃ x,¬ P(x)))
- (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x) est satisfiable et non valide. On se donne un domaine avec un seul élément a.
-
Si on choisit une interprétation avec PI(a) faux et QI(a) vrai, on a (∃ x,¬ P(x)) vrai et ∃ x,¬ Q(x) faux donc la formule est fausse dans cette interprétation donc non-valide.
- Si on choisit une interprétation avec QI(a) faux alors ∃ x,¬ Q(x) est vraie donc la formule est vraie dans cette interprétation donc satisfiable.
- (∃ x,¬ P(x)) ∧ (∀ x,P(x)) est insatisfiable. On peut s’appuyer sur la loi de de Morgan qui dit que ¬ ∃ x,¬ P(x)≡ ∀ x,P(x)
A.2 Exercices du chapitre 2
Exercice 1
Dans chacune des interprétations (qui fixent le domaine et sur ce domaine le sens des symboles ≤, < et ×), chaque formule a une valeur de vérité V ou F qu’il convient de justifier.
-
∀ x, ∃ y, x < y
-
Cette formule est vraie dans les trois interprétations ℕ, ℤ et ℚ. En effet si on se donne n’importe quelle valeur n pour x, il suffit de choisir la valeur n+1 pour y. Le résultat découle du fait que n<n+1 dans les trois interprétations.
- ∀ x, ∃ y, y < x
-
Cette formule est fausse dans l’interprétation ℕ. En effet si on choisit la valeur 0 pour x, quelle que soit n∈ℕ pour y, la propriété n<0 est toujours fausse.
- Cette formule est vraie dans les deux interprétations ℤ et ℚ. En effet si on se donne n’importe quelle valeur n pour x, il suffit de choisir la valeur n−1 pour y. Le résultat découle du fait que n−1<n dans les deux interprétations.
- ∀ x y, x < y ⇒ x+1 ≤ y
-
Cette formule est vraie dans les deux interprétations ℕ et ℤ. En effet si on se donne n’importe quelles valeurs n et m pour x et y, si x<y est vrai alors n<m et donc 0<m−n∈ℕ. Un entier strictement positif est supérieur ou égal à 1, donc 1≤ <m−n donc n+1≤ m. Ceci établit donc le résultat.
- Cette formule est fausse dans l’interprétation ℚ. En effet si on choisit la valeur 0 pour x,et la valeur 0,5 pour y, on a bien x<y qui est vrai car 0<0,5 mais x+1≤ y est faux car correspond 1≤ 0.5.
- ∀ x y z, x ≤ y ⇒ x× z ≤ y × z
-
Cette formule est vraie dans l’interprétation ℕ. En effet si on se donne n’importe quelles valeurs n et m et p dans ℕ pour x, y et z, si x≤ y est vrai dans cet environnement alors n≤ m, comme p ∈ℕ (donc positif), on a n× p≤ m× p et donc x× z ≤ y × z est vrai ce qui établit le résultat.
- Cette formule est fausse dans les interprétations ℤ et ℚ. En effet si on choisit la valeur 0 pour x, la valeur 1 pour y et la valeur −1 pour z. On a bien x≤ y est vrai car 0≤ 1. Mais x× z ≤ y × z est faux car correspond à 0≤ −1.
Exercice 2
-
La formule (∃ x,¬ P(x)) ⇒ ¬ ∀ x,P(x) est valide. On peut justifier cela avec les lois de de Morgan, car ¬ ∀ x,P(x) ≡ ∃ x,¬ P(x) et donc la formule est un cas particulier de A⇒ A qui est une tautologie. On peut aussi montrer le résultat en revenant à la définition des interprétations.
Si on se donne une interprétation I sur un domaine D telle que ∃ x,¬ P(x) est vrai dans cette interprétation alors il existe d∈ D, tel que ¬ P(x) est vrai dans cette interprétation et dans l’environnement dans lequel la variable x a la valeur d. On a donc P(x) faux dans l’interprétation I et le même environnement. On en déduit que ∀ x, P(x) faux dans l’interprétation I et donc ¬ ∀ x, P(x) est vrai.
Si on part de la formule ∃ x,¬ P(x) ⇒ ¬ ∀ x,P(x) qui se parenthèse comme ∃ x,(¬ P(x) ⇒ ¬ ∀ x,P(x)), le résultat est le même. Cette formule est valide. On peut le montrer en utilisant le fait que ∃ x,(¬ P(x) ⇒ ¬ ∀ x,P(x)) ≡ (∀ x,¬ P(x)) ⇒ ¬ ∀ x,P(x) et que si ∀ x,¬ P(x) est vrai alors a fortiori ∃ x,¬ P(x) est vrai puis se ramener au cas précédent. On peut aussi faire un raisonnement direct avec une interprétation I sur un domaine D. On choisit n’importe quel d∈ D (possible car D≠∅). On doit montrer que ¬ P(x)⇒ ¬ ∀ x,P(x) est vraie dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d. On conclut de la même manière que précédemment.
- La formule (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x) est satisfiable. Il suffit de prendre une interprétation sur un domaine D formé d’un seul élément a et telle que l’interprétation de Q est l’ensemble vide. On a donc que Q(x) est faux dans l’environnement dans lequel la variable x a la valeur a, donc ¬ Q(x) est vraie et donc aussi ∃ x,¬ Q(x) et finalement (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x).
La formule (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x) est non valide. Il faut pour cela trouver une interprétation qui rend fausse la formule, donc qui rend vraie ∃ x,¬ P(x) et fausse ∃ x,¬ Q(x). On peut à nouveau prendre une interprétation sur un domaine D formé d’un seul élément a et telle que l’interprétation de P est l’ensemble vide et l’interprétation de Q est l’ensemble D tout entier.
Le résultat est le même avec le parenthésage ∃ x,(¬ P(x) ⇒ ∃ x,¬ Q(x)), la formule est satisfiable mais non valide.
- La formule (∃ x,¬ P(x)) ∧ ∀ x,P(x) est insatisfiable. Il faut montrer qu’elle est fausse dans toutes les interprétations. Pour cela on se donne une interprétation I sur un domaine D quelconque. Si la formule était vraie dans cette interprétation, on aurait ∃ x,¬ P(x) et donc on aurait que ¬ P(x) est vrai dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d. On aurait donc que P(x) est faux dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d ce qui contredit le fait que ∀ x,P(x) est vrai.
On peut aussi utiliser les lois de de Morgan ¬ ∀ x,P(x)≡ ∃ x, ¬ P(x) ce qui montre que la formule est équivalente à (¬ ∀ x,P(x)) ∧ (∀ x,P(x)) qui est une instance de la formule propositionnelle ¬ A ∧ A qui est insatisfiable.
Le résultat est le même avec le parenthésage ∃ x,(¬ P(x) ∧ ∀ x,P(x)), on peut alors commencer par appliquer l’equivalence ∃ x,(¬ P(x) ∧ ∀ x,P(x)) ≡ (∃ x,¬ P(x)) ∧ (∀ x,P(x)) car ∀ x,P(x) ne dépend pas de x, ce qui nous ramène au cas précédent.
Exercice 3
On a ⊥⇒ P≡⊤, ⊤⇒ P≡ P, P⇒ ⊤≡⊤. On peut justifier par des tables de vérité ou bien utiliser A⇒ B≡ ¬ A∨ B et utiliser les lois connues pour les connecteurs ⊥, ⊤ et ∨.
Exercice 4
On suppose que x∉VL(A).
- ∀ x,(A ⇒ H(x)) ≡ ∀ x,(¬ A ∨ H(x))≡ ¬ A ∨ ∀ x,H(x)≡
A ⇒ ∀ x, H(x)
- ∃ x,(A ⇒ H(x)) ≡∃ x,(¬ A ∨ H(x))≡ ¬ A ∨ ∃ x,H(x)≡
A ⇒ ∃ x, H(x)
- ∀ x,(G(x) ⇒ A) ≡ ∀ x,(¬ G(x) ∨ A)≡ (∀ x,¬ G(x)) ∨ A
≡¬ (∃ x, G(x)) ∨ A
≡ (∃ x, G(x)) ⇒ A
- ∃ x,(G(x) ⇒ A) ∃ x,(¬ G(x) ∨ A)≡ (∃ x,¬ G(x)) ∨ A
≡¬ (∀ x, G(x)) ∨ A≡ (∀ x, G(x)) ⇒ A
Exercice 5
Trouver des interprétations qui justifient les résultats suivants :
-
∀ x, ∃ y,R(x,y) ≢∃ y,∀ x, R(x,y)
On a ∃ y,∀ x, R(x,y)⊨ ∀ x, ∃ y,R(x,y) mais le sens inverse est faux
∀ x, ∃ y,R(x,y) ⊭∃ y,∀ x, R(x,y).
Pour montrer ce résultat, il suffit de trouver une interprétation dans laquelle ∃ y,∀ x, R(x,y) est vraie et ∀ x, ∃ y,R(x,y) est fausse.
Il suffit de prendre une interprétation avec un domaine qui contient deux éléments 0 et 1 avec pour la relation R la relation d’égalité. On a x=x et 0≠1
- ∀ x, (G(x)∨ H(x)) ≢(∀ x,G(x)) ∨ (∀ x,H(x))
On a (∀ x,G(x)) ∨ (∀ x,H(x))⊨ ∀ x, (G(x)∨ H(x)) mais le sens inverse est faux ∀ x, (G(x)∨ H(x)) ⊭(∀ x,G(x)) ∨ (∀ x,H(x))
Pour montrer ce résultat, il suffit de trouver une interprétation dans laquelle ∀ x, (G(x)∨ H(x)) est vraie et (∀ x,G(x)) ∨ (∀ x,H(x)) est fausse.
Il suffit de prendre une interprétation avec un domaine qui contient deux éléments 0 et 1 et dans laquelle G est vraie pour 0 et faux pour 1 et H est faux pour 0 et vraie pour 1. Dans cette interprétation on a bien ∀ x, (G(x)∨ H(x)) est vrai mais ∀ x,G(x) et ∀ x,H(x) sont faux.
- ∃ x, (G(x)∧ H(x)) ≢(∃ x,G(x)) ∧ (∃ x,H(x))
On a ∃ x, (G(x)∧ H(x)) ⊨ (∃ x,G(x)) ∧ (∃ x,H(x)) mais le sens inverse est faux (∃ x,G(x)) ∧ (∃ x,H(x)) ⊭∃ x, (G(x)∧ H(x))
On prend la même interprétation que dans le cas précédent. On a bien ∃ x,G(x) est vrai (prendre x↦ 0 et ∃ x,H(x) est vrai (prendre x↦ 1) et donc leur conjonction est vraie. Par contre ∃ x, (G(x)∧ H(x)) est faux car aucun des éléments du domaine ne rend vraie la formule.
Exercice 6
Le langage contient n constantes {c1;…;cn}. On note I,ρ⊨ A lorsque la formule A est vraie dans l’interprétation I et l’environnement ρ, c’est-à-dire lorsque valI(ρ, A)=V.
On s’intéresse aux interprétations dans lesquelles le symbole d’égalité est interprété par l’égalité dans le domaine. C’est-à-dire que
I,ρ⊨ t=u si et seulement si valI(ρ,t)=valI(ρ,u)
-
Le cardinal du domaine d’une interprétation qui rend vraie la formule ∀ x, x=c1∨… ∨ x=cn est inférieur ou égal à n. En effet la formule dit que tout élément du domaine est égal à l’interprétation d’une des constantes ci ce qui fait qu’il y a au plus n valeurs possibles. Par contre rien n’empêche deux constantes différentes d’être interprétées par la même valeur dans le domaine, donc on peut avoir strictement moins de n éléments.
Pour justifier le résultat plus formellement, on se donne une interprétation I sur un domaine D et on appelle C l’ensemble des interprétations des constantes {c1;…;cn}, à savoir C={valI(ci)|1≤ i≤ n}. On a C ⊆ D et |C|≤ n. On va montrer que D=C.
Soit donc d∈ D. Comme I⊨ ∀ x, x=c1∨… ∨ x=cn on a I,{x↦ d} ⊨ x=c1∨… ∨ x=cn et donc comme une disjonction est vraie lorsque l’une des parties est vraie, il existe i tel que I,{x↦ d} ⊨ x=ci et donc d=valI({x↦ d},x)=valI({x↦ d},ci) et donc d∈ C.
Les deux ensembles étant égaux ont même cardinal qui est inférieur à n.
- Montrons que (∀ x, x=c1∨… ∨ x=cn), (P(c1) ∧ … ∧ P(cn)) ⊨ ∀ x, P(x)
On se donne une interprétation I de l’égalité et telle que I⊨ ∀ x y, x=y ⇒ (P(x)⇒ P(y)), I⊨ ∀ x, x=c1∨… ∨ x=cn et I⊨ P(c1) ∧ … ∧ P(cn). Soit d∈ D.
On a I,{x↦ d} ⊨ x=c1∨… ∨ x=cn donc il exists i tel que I,{x↦ d} ⊨ x=c1, on a aussi I,{x↦ d}⊨ P(ci) on en déduit que I,{x↦ d}⊨ P(x) et donc I⊨ ∀ x,P(x).
On pourrait faire le même raisonnement pour l’existentielle. On peut aussi réutiliser le résultat précédent.
On peut remplacer P(x) par ¬ P(x) en utilisant la propriété 3 de remplacement d’un symbole de prédicat par une formule paramétrée. On a donc (∀ x, x=c1∨… ∨ x=cn), (¬ P(c1) ∧ … ∧ ¬ P(cn)) ⊨ ∀ x, ¬ P(x)
On utilise ensuite le fait que pour tout ensemble de formule E et deux formules A et B, E,A⊨ B est équivalent à E,¬ B⊨ ¬ A (on peut utiliser le fait que E,A⊨ B est équivalent à E⊨ A ⇒ B et la propriété de contraposée A ⇒ B≡¬ B⇒¬ A ).
Exercice 7
-
Il suffit d’introduire une constante c et de prendre
comme formule A la formule ∀ x, x=c
- On a (cas particulier de l’exercice précédent) ∀ x, x=c⊨ (∀ x,P(x)) ⇔ P(c) et ∀ x, x=c⊨ (∃ x,P(x)) ⇔ P(c) on en déduit que ∀ x, x=c⊨ (∀ x,P(x)) ⇔ (∃ x,P(x))
- S’il y a deux éléments a,b dans le domaine, on choisit une interprétation I telle que I,{x↦ a}⊨ P(x) et
I,{x↦ b}⊭P(x). On a bien I ⊨ ∃ x, P(x) mais I ⊭∀ x, P(x)
Exercice 8
Soit la formule ∀ x y, (P(x)∧ Q(y) ∧ (¬ P(a) ∨ ¬ Q(a))). Le langage des termes ne contient que la constante a, celui des prédicats contient les deux symboles P et Q.
-
Le domaine de Herbrand est l’ensemble des termes clos, ici réduit à la constante a.
- La base de Herbrand est l’ensemble des formules atomiques closes, ici réduite à deux formules P(a) et Q(a).
- Il y a quatre interprétations possibles suivant que P(a) et Q(a) valent vrai ou faux.
- La formule est universelle, elle est satisfiable si et seulement si l’ensemble de ses instances closes est satisfiable. Ici il y a une seule instance close P(a)∧ Q(a) ∧ (¬ P(a) ∨ ¬ Q(a)).
On peut faire une table de vérité
|
| | P(a) | Q(a) | P(a)∧ Q(a) ∧ (¬ P(a) ∨ ¬ Q(a)) |
| F | _ | F |
| V | F | F |
| V | V | F |
| |
|
La formule est fausse dans tous les modèles de Herbrand, elle est universelle et donc, d’après le théorème de Herbrand, elle est fausse dans n’importe quelle interprétation et elle est donc insatisfiable.
Exercice 9
-
La formule (∃ x,P(x))⇒∀ x,P(x) n’est pas valide (contre exemple avec un modèle à deux élements)
- La négation de cette formule, notée B est (∃ x,P(x))∧ ∃ x,¬ P(x)
- Il n’y a pas de constante dans le langage, on en ajoute une a et le domaine de Herbrand est réduit à cette constante a. La base de Herbrand contient une formule atomique P(a) et il y a donc deux interprétations possibles suivant que P(a) est vraie ou fausse.
- Il n’y a pas de modèle de Herbrand qui rend vraie la formule B.
- On ne peut pas appliquer le théorème de Herbrand car la formule n’est pas universelle. D’ailleurs la formule est satisfiable (on peut construire un modèle avec deux éléments ou dire que si elle était satisfiable alors sa négation serait valide, ce qui n’est pas le cas comme montré à la question 1).
A.3 Exercices du chapitre 3
Exercice 1
-
La fonction clauseset prend pour argument un ensemble
d’instances de prédicats associés à des booléens et renvoie une
formule de la logique correspondant à la clause associée.
| clauseset(s) =
| | si s=∅
alors ⊥ |
| sinon | | soit (p,b)∈ s,s′=s\ (p,b),
A=si b alors p sinon ¬
p |
| dans si s′=∅ alors A sinon A∨clauseset(s′) |
|
|
|
Exercice 2
A =def (∃ x, ∀ y, R(x,y)) ⇒ (∀ y, ∃ x, R(x,y)).
-
La forme normale de négation de la formule ¬ A est
(∃ x, ∀ y, R(x,y))∧ (∃ y, ∀ x, ¬ R(x,y))
- La forme de skolem de la formule ¬ A introduit deux constantes a et b
(∀ y, R(a,y))∧ ∀ x, ¬ R(x,b)
- La forme clausale de ¬ A a deux clauses {R(a,y);¬ R(x,b)}
- L’ensemble des instances clauses contient {R(a,b);¬ R(a,b)} qui est insatisfiable.
La formule ¬ A est donc insatisfiable et la formule A est valide.
A.4 Exercices du chapitre 4
Exercice 1
-
N(x,є)=? N(є,y)
Solution : {x← є;z← є}
- N(N(x,y),є) =? N(є,y)
Pas de solution : on simplifie en utilisant (7) qui amène l’équation N(x,y)=?є qui échoue (règle 6).
- N(x,є) =? x
Pas de solution : échec règle (3) après avoir appliqué la règle (5) pour retourner l’équation.
Exercice 4
Il suffit de résoudre le problème :
{t1=? t2;t2=? t3 … tn−1=? tn}
On peut se ramener à une seule équation :
F(t1,t2,…,tn−1)=F(t2,t3, …,tn)
Exercice 3
-
(plus(x,0)=x)=? (plus(0,y)=y)
Solution {x← 0;y← 0}
- (plus(x,0)=x)=? y ≠ z
Pas de solution car un littéral positif ne peut être égal à un littéral négatif.
- (plus(x,0)=x)=? (y=plus(y,0))
Pas de solution : le problème se décompose en
plus(x,0)=? y; x =? plus(y,0) qui se simplifie par les règles (5) puis (4),on obtient {y← plus(x,0)}(x =? plus(plus(x,0),0)) qui conduit à un échec suivant la règle (3).
Exercice 5
-
On peut changer l’ordre des motifs, les exécuter en parallèle lorsque :
inst(pi) ∩ inst(pj) = ∅
- Tous les cas sont couverts si
inst(p1) ∪ … ∪ inst(pn) = T(F)
- Le motif pj est inutile si
inst(pj) ⊆ inst(p1) ∪ … ∪ inst(pj−1)
Exercice 7
Pour prouver (∃ x,¬ P(x)), (∀ x,(P(x) ∨
Q(x)))⊨ ∃ x, Q(x) en utilisant la résolution, on procède aux étapes suivantes :
-
Mise en forme clausale
- Résolution :
- Conclusion : ¬ A est insatisfiable donc A est valide.