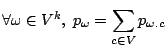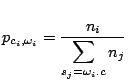


Next: The GRAMMAR package: Context-Free
Up: GenRGenS v2.0 User Manual
Previous: Generalities and file formats
Contents
Subsections
The MARKOV package : Markovian models
Markovian models are the simplest, easiest to use statistical models available for genomic sequences.
Statistical properties associated with a Markovian model make it become a valuable tool to the one who wants
to take into account the occurrences of 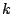 -mers in a sequence.
Their most commonly used version, the so-called classical Markovian models, can be automatically built
from a set of real genomic sequences. Hidden Markovian models are now supported by
GenRGenS at the cost of some preprocessing, as shown in section 3.1.3.
Apart from genomics, such models appear in various scientific fields including-but-not-limited-to
speech recognition, population processes, queuing theory and search engines3.1.
-mers in a sequence.
Their most commonly used version, the so-called classical Markovian models, can be automatically built
from a set of real genomic sequences. Hidden Markovian models are now supported by
GenRGenS at the cost of some preprocessing, as shown in section 3.1.3.
Apart from genomics, such models appear in various scientific fields including-but-not-limited-to
speech recognition, population processes, queuing theory and search engines3.1.
Main definition
Formally, a classical Markovian model applied to a set of random variables
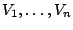 causes the probabilities associated
with the potential values for
causes the probabilities associated
with the potential values for 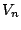 to depend on the values of
to depend on the values of
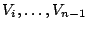 . We will focus on homogenous Markovian
models, where the probabilities for the different values for
. We will focus on homogenous Markovian
models, where the probabilities for the different values for 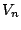 are conditioned by the values already chosen for a small subset
are conditioned by the values already chosen for a small subset
![$ [V_{i-k-1},V_{i-1}]$](img25.gif) of variables from the past, also called context of
of variables from the past, also called context of 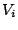 . The parameter
. The parameter 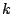 is called the order
of the Markovian model. Moreover, the probabilities of the values for
is called the order
of the Markovian model. Moreover, the probabilities of the values for 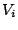 in an homogenous Markovian model cannot in any way be
conditioned by the index
in an homogenous Markovian model cannot in any way be
conditioned by the index 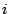 of the variable.
of the variable.
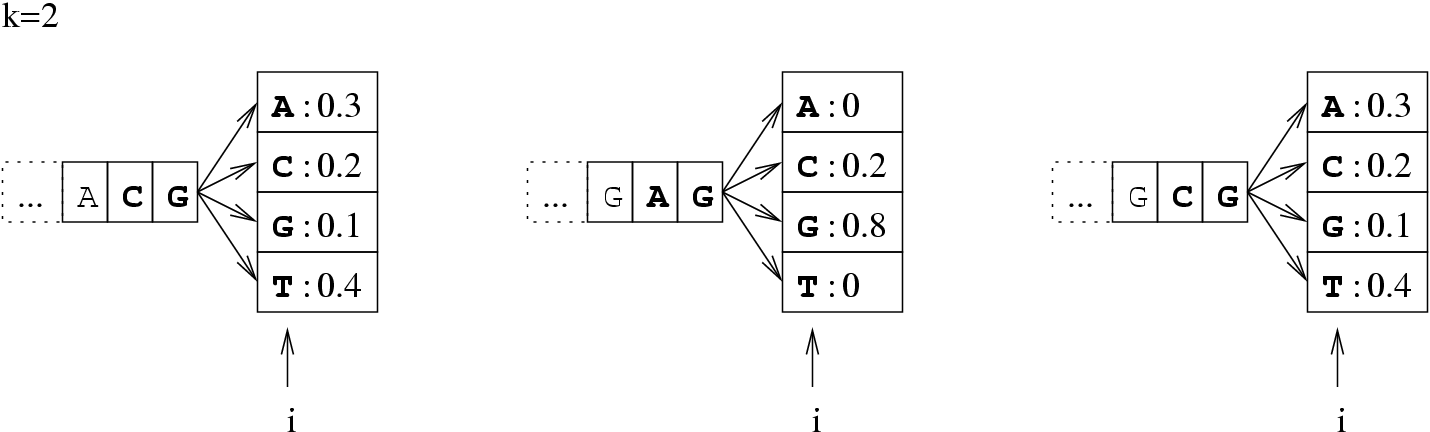
Figure 3.1:
The probability of the event : "the 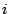 -th base is an
-th base is an 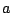 " depends on its
" depends on its 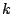 predecessors.
predecessors.
|
|
Applied to genomic sequences, the random variable 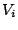 stands for the
stands for the 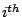 base in the sequence. The Markovian model
constrains the occurrence probability for a base
base in the sequence. The Markovian model
constrains the occurrence probability for a base 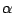 in a given context composed of the
in a given context composed of the 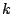 previously assigned
letters, therefore weakly3.2! constraining the proportions of each
previously assigned
letters, therefore weakly3.2! constraining the proportions of each 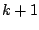 -mers.
-mers.
What about heterogeneity ?
GenRGenS handles a small subset of the heterogenous Markovian class of
models.
Formally, an heterogenous model allows the probabilities
associated with a variable 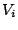 to depend on any of the variables prior to
to depend on any of the variables prior to 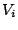 . Our subset of the heterogenous Markovian
models will use an integer parameter called
. Our subset of the heterogenous Markovian
models will use an integer parameter called 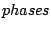 to compute the probabilities for
to compute the probabilities for 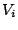 . The phase of a variable
. The phase of a variable 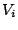 is simply given by the formula
is simply given by the formula
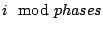 . In our subset of the heterogenous Markovian models, the
probabilities for
. In our subset of the heterogenous Markovian models, the
probabilities for 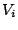 depend on both context and phase of the variable. Such an addition is useful to model
phenomenons in which variables are gathered in packs of
depend on both context and phase of the variable. Such an addition is useful to model
phenomenons in which variables are gathered in packs of 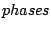 consecutive variables, and their values not only
depend of their contexts, but also of their relative position inside the pack. Such are sequences of protein-coding DNA, where
the position of a base inside of a base triplet is well-known to be of interest.
consecutive variables, and their values not only
depend of their contexts, but also of their relative position inside the pack. Such are sequences of protein-coding DNA, where
the position of a base inside of a base triplet is well-known to be of interest.
It is also possible to simulate such phase alternation by introducing dummy letters encoding the phase
in which they will be produced. For instance, an order 0 model having 3 phases (for coding DNA...) would
result in a sequence model over the alphabet {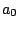 ,
,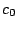 ,
,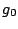 ,
,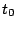 ,
,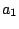 ,
,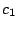 ,
,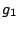 ,
,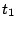 ,
,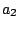 ,
,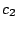 ,
,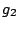 ,
,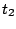 }
having non-null transition probabilities only for
}
having non-null transition probabilities only for
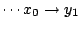 ,
,
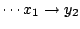 and
and
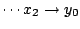 .
Therefore, the expressivity of our heterogenous models do not
exceed that of the homogenous ones, but it is much more convenient
to write these models using an heterogenous syntax.
.
Therefore, the expressivity of our heterogenous models do not
exceed that of the homogenous ones, but it is much more convenient
to write these models using an heterogenous syntax.
Hidden Markovian Models (HMMs)
Hidden Markovian models address the hierarchical decomposability of most sequences.
An hidden Markovian model is a combination of a top-level Markovian model and a set of bottom-level Markovian models,
called hidden states. The generation process associated with an HMM initiates the sequences using a random hidden state.
At each step of the generation, the algorithm may switch to another hidden using probabilities from the top-level model,
and then emits a symbol using probabilities related to the current urn.
Once again, this class of models' expressivity seems to exceed that of the classical Markovian models.
However, in our context, it is possible to emulate an hidden model with a
classical one just by duplicating the alphabet so that the emitted character also contains the state
which it belongs to.
This section describes the syntax and semantics of Markovian description files, as shown in figure 3.2.
Figure 3.2:
Main structure of a Markovian description file
![\begin{figure}
\begin{center}
\texttt{\begin{tabular}{l}
TYPE = MARKOV \\ ...
.....\\ [0.1cm]
[ALIASES = ...]
\end{tabular}}
\end{center}
\end{figure}](img47.gif) |
Clauses nested inside square brackets are optional. The given order for the clauses is mandatory.
Markovian description files allows definition of the Markovian model parameters.
ORDER = 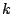
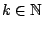
Required
Sets the order of the underlying Markovian model to a positive integer value 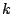 .
The order of a Markovian model is the number of previously emitted symbols taken into account
for the emission probabilities of the next symbol.
See section 3.1.1 for more details about this parameter.
.
The order of a Markovian model is the number of previously emitted symbols taken into account
for the emission probabilities of the next symbol.
See section 3.1.1 for more details about this parameter.
PHASE = 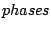
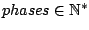
Optional, defaults to PHASE = 0
Sets the number of phases parameter of GenRGenS' heterogenous Markovian models subclass to a positive non-null integer value 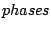 .
See section 3.1.2 for more details about this parameter.
.
See section 3.1.2 for more details about this parameter.
SYMBOLS = {WORDS,LETTERS}
Optional, defaults to SYMBOLS = WORDS
Chooses the type of symbols to be used for random generation.
When WORDS is selected, each pair of symbols must be separated by at least a blank character (space, tabulation or newline). A Markovian
description file written using WORDS will then be easier to read, as explicit names for symbols can be used, but may take a little longer
to write, as illustrated by the toy example of the FREQUENCIES clause's content for a simple
Markovian description file modelling the ORF/Intergenic alternation at a base-triplet level
:
Figure 3.3:
A simple Markovian model for the Intergenic/ORF
alternation
 |
A LETTER value for the SYMBOLS parameter will force GenRGenS to see a word as a sequence of symbols. For instance,
the definition of a 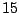 /
/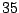 /
/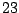 /
/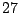 occurrences proportions for the symbols A/C/G/T in a context ACC
will be expressed by the following statement inside of the FREQUENCIES clause :
Optional, defaults to the distribution of k-mers, k being the value
occurrences proportions for the symbols A/C/G/T in a context ACC
will be expressed by the following statement inside of the FREQUENCIES clause :
Optional, defaults to the distribution of k-mers, k being the value 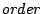 (see below).
(see below).
Defines the frequencies associated with various eligible prefixes for the generated sequence.
Each 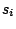 is either a sequence of symbols separated by white spaces or a word, depending on the value
of the SYMBOLS parameter. Every
is either a sequence of symbols separated by white spaces or a word, depending on the value
of the SYMBOLS parameter. Every 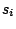 must be composed of the same amount
must be composed of the same amount 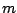 of symbols,
of symbols,
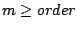 .
.
If omitted, the beginning of the sequence is chosen according to the distribution of k-mers implied by
the content of the FREQUENCIES clause and computed as follows :
where 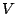 is the set of symbols used inside of the sequence,
is the set of symbols used inside of the sequence, 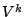 is the set of words of size
is the set of words of size 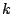 , and
, and
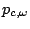 is the probability
of emission of
is the probability
of emission of 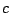 in a context
in a context 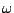 as defined by the FREQUENCIES clause. Note that no specific order is required
for definition of a START clause.
This clause is used to define the probabilities of emission
of the Markovian model.
Required
as defined by the FREQUENCIES clause. Note that no specific order is required
for definition of a START clause.
This clause is used to define the probabilities of emission
of the Markovian model.
Required
Defines the probabilities of emission for the different symbols.
Each 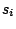 is either a sequence of symbols separated by white spaces or a word, depending on the value
of the SYMBOLS parameter. Each
is either a sequence of symbols separated by white spaces or a word, depending on the value
of the SYMBOLS parameter. Each 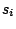 is composed of
is composed of 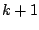 symbols,
symbols, 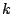 being the order. The first
being the order. The first 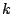 symbols define the context
and the last letter a candidate to emission. The relationship between the frequency definition
symbols define the context
and the last letter a candidate to emission. The relationship between the frequency definition 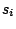
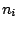 and the probability
and the probability
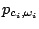 of emitting
of emitting 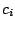 in a context
in a context 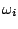 ,
,
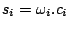 is given by the following formula :
The (simple) idea behind this formula is that the probability of emission of a base in a certain context equals to the context/base,
concatenation's frequency divided by the sum of the frequencies sharing the same context .
Choice has been made to write frequencies instead of direct probabilities because most of the Markovian models encountered in genomics are
built from real data by counting the occurrences of all
is given by the following formula :
The (simple) idea behind this formula is that the probability of emission of a base in a certain context equals to the context/base,
concatenation's frequency divided by the sum of the frequencies sharing the same context .
Choice has been made to write frequencies instead of direct probabilities because most of the Markovian models encountered in genomics are
built from real data by counting the occurrences of all 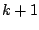 -mers, thus allowing the direct injection of the counting process' result
into the description file. As for the START clause, it is not necessary to provide values for the FREQUENCIES in a specific
order.
-mers, thus allowing the direct injection of the counting process' result
into the description file. As for the START clause, it is not necessary to provide values for the FREQUENCIES in a specific
order.
HMMFREQUENCIES = 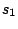
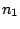
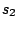
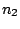
 ;
;
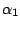 :
: 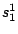
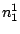
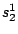
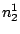
 ;
;
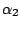 :
: 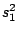
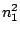
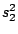
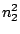
 ;
;
 ;
;
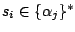 ,
,
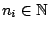 ,
,
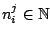
Required
Defines the hidden Markovian model's probabilities of
emission.
First, a master model 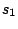
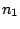
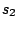
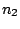
 is
defined for the alternation of the hidden states.
is
defined for the alternation of the hidden states. 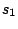 ,
, 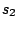 ,
, 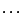 are
sequences of hidden states
are
sequences of hidden states 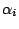 , separated or not by whitespaces depending on the
previously defined value for the clause SYMBOLS.
, separated or not by whitespaces depending on the
previously defined value for the clause SYMBOLS. 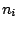 are sequences of integers,
representing the frequencies of the corresponding sequence. Their lengths equal the phase parameter of the
model, as provided by the PHASE clause.
are sequences of integers,
representing the frequencies of the corresponding sequence. Their lengths equal the phase parameter of the
model, as provided by the PHASE clause.
Then, a model definition is required for each hidden states 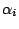 through the following syntax:
Each
through the following syntax:
Each 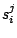 is composed of symbols
is composed of symbols 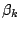 , which are part of the emission vocabulary.
, which are part of the emission vocabulary.
Once such a model is defined, a sequence is issued starting from a random hidden state 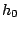 . At each step
. At each step 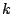 of the generation, the process is allowed to move from the current hidden state
of the generation, the process is allowed to move from the current hidden state 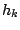 to another hidden state
to another hidden state 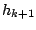 (potentially
(potentially
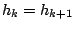 ) and then emits a symbol according to the probabilities of the hidden state
) and then emits a symbol according to the probabilities of the hidden state 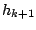 .
The process is iterated until the expected number of symbols are generated.
.
The process is iterated until the expected number of symbols are generated.
Remark 1: Each model definition must be ended by a semicolon ; to avoid ambiguity.
Remark 2: The vocabularies
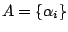 and
and
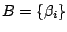 respectively used
for the master and the hidden states model definition must be disjoint.
respectively used
for the master and the hidden states model definition must be disjoint.
Remark 3: The numbers of phases for heterogenous master and hidden states model must be equal.
Remark 4: Different orders for the master and states models are supported.
We illustrate the design of a Markovian model with a description file generated automatically from the 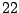 -th human chromosome, using the tool
BuildMarkov bundled with GenRGenS and described in section 3.4.2, through the following command:
-th human chromosome, using the tool
BuildMarkov bundled with GenRGenS and described in section 3.4.2, through the following command:
java -cp . GenRGenS.markov.BuildMarkov -o 0 -p 1 q22.fasta -d q22.ggd
This model is a Bernoulli one, as no memory is involved here, i.e. the probability of emission of a base doesn't depend on events from the past.
Figure 3.4:
A Bernoulli model for the entire 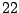 -th human chromosome(cleaned up from unknown N bases.)
-th human chromosome(cleaned up from unknown N bases.)
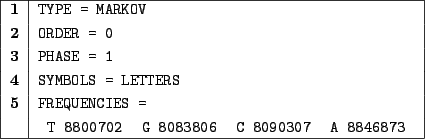 |
In 1, we choose a Markovian random generation.
In 2, we choose an amnesic model, i.e. there is no relation between two bases probabilities.
In 3, we choose an homogenous model, the probabilities of emission won't depend on the index of the symbol
among the sequence.
In 4, we use letters as symbols for simplicity sake.
Clause 5 provides definition for the frequencies. Here, the A and T are slightly more likely
to occur than C and G. Precisely, at each step an A symbol will be emitted with probability
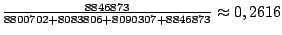 .
This description file has been built automatically from a portion of the
.
This description file has been built automatically from a portion of the 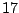 q
q part of the 17-th human chromosome by
the tool BuildMarkov invoked through the following command:
part of the 17-th human chromosome by
the tool BuildMarkov invoked through the following command:
java -cp . GenRGenS.markov.BuildMarkov -o 1 -p 1 17-q11.fasta -d 17-q11.ggd
Figure 3.5:
Order 1 Markov model for the sequence of the mRNA encoding the S-protein involved in serum spreading.
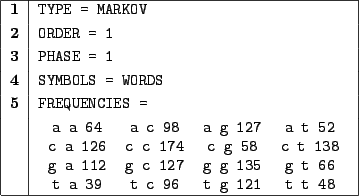 |
In 1, we choose a Markovian random generation.
In 2, we choose an order 1 model, i.e. the probability of emission of a symbol only depends on the symbol
immediately preceding in the sequence.
In 3, we choose an homogenous model, the probabilities of emission won't depend on the index of the symbol
among the sequence.
In 4, we illustrate the use of WORDS. The symbols must be separated in the FREQUENCIES by
at least one whitespace or carriage return. Space characters will be inserted between symbols in the output.
Clause 5 provides definition for the frequencies, subsequently for the transition/emission probabilities.
The following description file describes a Markovian model for the first chromosome's  q
q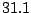 area of the human genome,
built by BuildMarkov through :
area of the human genome,
built by BuildMarkov through :
java -cp . GenRGenS.markov.BuildMarkov -o 2 -p 3 1q31.1.fasta -d 1q31.1.ggd
and edited afterward to include the START clause.
Figure 3.6:
A Markovian description file for the  q
q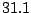 area of the first human
chromosome
area of the first human
chromosome
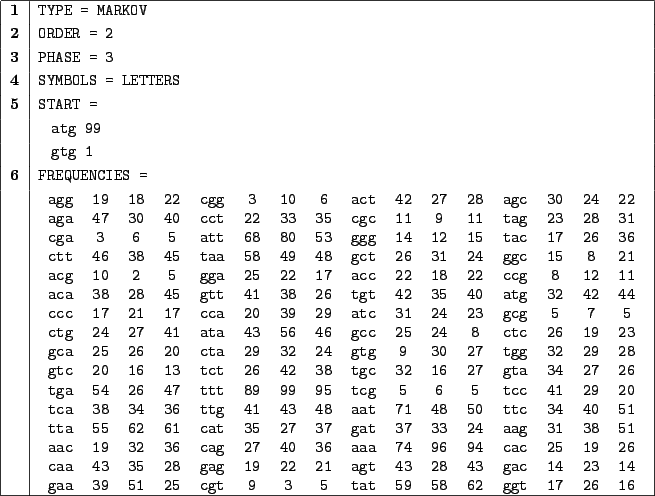 |
In 1, we choose a Markovian random generation.
In 2, we will consider the frequencies of
base triplets, e.g. the probability of emission of a base is conditioned by the  last bases.
last bases.
In 3, we differentiate the behaviour of the Markovian process for each phase, in order
to capture some properties of the coding DNA.
In 4, we use letters as symbols for simplicity sake.
Clause 5 initiates each sequence
with an atg base triplet with probability 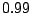 or chooses gtg with probability
or chooses gtg with probability 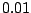 .
.
Clause 6 provides definition for the frequencies. To explain the semantics of this clause, we will
focus on some particular frequencies definitions :
agg 19 18 22 aga 47 30 40 agt 43 28 43 agc 30 24 22
Writing agg 19 means that base g has occurred 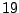 times in an ag context on phase 0.
In other words, the motif agg has occurred
times in an ag context on phase 0.
In other words, the motif agg has occurred 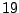 times on phase
times on phase 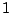 . We will illustrate the link with the emission
probability of g in a context ag in the next section.
. We will illustrate the link with the emission
probability of g in a context ag in the next section.
- -
- First a random start atg is chosen with probability
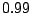 .
.
- -
- The context, here composed of the two most recently emitted bases, is now tg, and the phase3.3
of the next base is
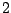 . The emission probabilities for the bases of a g is
. The emission probabilities for the bases of a g is
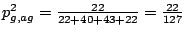 .
Similarly, probabilities of emissions for the other bases are
.
Similarly, probabilities of emissions for the other bases are
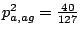 ,
,
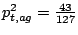 and
and
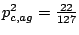 .
.
- -
- After a call to a random number generator, a g base is chosen and emitted.
- -
- The new context is then gg, and the new phase is 0. We then consider new
probabilities for the bases a,c,g and t:
gga 25 22 17 ggc 15 8 21 ggg 14 12 15 ggt 17 26 16
The probabilities of emission for the different bases are then
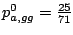 ,
,
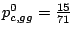 ,
,
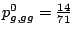 and
and
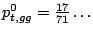
Figure 3.7:
Basic HMM excerpted from the sequence
analyst's bible[6]
|
|
Consider the basic output of a HMM profile building algorithm drawn in Figure 3.7.
It can be translated into the following
GenRGenS input file:
Figure 3.8:
A Markovian description file for the  q
q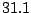 area of the first human
chromosome
area of the first human
chromosome
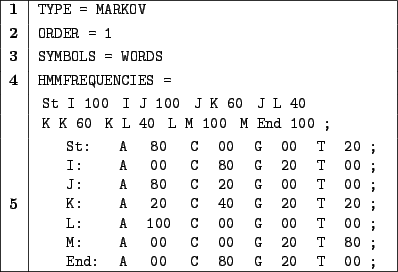 |
In 1, we choose a Markovian random generation.
In 2, an order of  is defined for the master model.
is defined for the master model.
In 3, we choose to manipulate words as symbols.
Part 4 is a definition for the frequencies of the master Markovian model. For instance, the probability of choosing
L as the next hidden state while in state J is
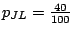 .
.
Remark: The word
START is a keyword and cannot be used as an identifier.
Part 5 contains the different emission frequencies, converted from probabilities to integers.
Inside some markovian models, it is theoreticaly possible that some states may be dead-ends, the frequencies
of all candidate symbols summing to 0 in this context. It is then impossible to emit an extra symbol. That is why
GenRGenS always checks weither each reachable state can be exited. The default behaviour of GenRGenS
is to refuse to generate sequences in such a case, as the generated sequences are supposed to be of the size provided
by the user, and it is senseless to keep on generating letters when a dead-end is encountered. However, this
phenomenon may be intentional, in order for instance to end the generation with a specific word (perhaps a STOP
codon...) if total control over the size can be neglected.
Markovian specific command line option usage:
java -cp . GenRGenS.GenRGenS -size n -nb k -m [T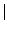 F] MarkovianGGDFile
F] MarkovianGGDFile
- -m [T
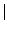 F]: Toggles rejection of models with dead-ends on (T) and off (F).
Notice that disabling the rejection may result in shorter sequences than that specified by mean of the size parameter.
Defaults to -m T.
F]: Toggles rejection of models with dead-ends on (T) and off (F).
Notice that disabling the rejection may result in shorter sequences than that specified by mean of the size parameter.
Defaults to -m T.
BuildMarkov: Automatic construction of MARKOV description files
This small software is dedicated to the automatic construction of MARKOV description files
from a sequence. It scans the sequence(s) provided through the command line and evaluates the
probabilities of transitions from and to each markov states.
After decompression of the GenRGenS archive, move to GenRGenSDir
and open a shell to invoke the Java virtual machine through the following command:
java -cp . GenRGenS.markov.BuildMarkov [options] InputFiles
where:
- -
- InputFiles is a set of paths aiming at sequences that will be used for Markov model construction. Required(At Least one).
The following parameters/options can also be specified :
- -d OutputFile: Outputs the description file to the file OutputFile.
- -p
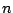 : Defines the number of phases in the markov model.
: Defines the number of phases in the markov model. 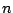 must be
must be 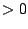 .
. 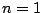 means that
the model will be homogenous. Defaults to
means that
the model will be homogenous. Defaults to 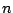 =1.
=1.
- -o
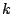 : Defines the order of the markov model.
: Defines the order of the markov model. 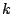 must be
must be 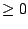 .
. 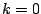 means that
the model will be a bernoulli model. Defaults to
means that
the model will be a bernoulli model. Defaults to 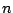 =0.
=0.
- -v
 : Verbose mode, show the progress of the construction(useful for large files).
: Verbose mode, show the progress of the construction(useful for large files).
The input files can be flat files, that are text files containing a raw sequence, or FASTA
formatted files, that are an alternation of title lines and sequences, and usually look like the figure below.
Figure 3.9:
A typical FASTA formatted file, containing several sequences.
 |
Remark1: Inside a sequence definition, both for FASTA and flat files,
BuildMarkov ignores the spaces, tabulations and carriage returns
so that the sequence can be indented in a user-friendly way.
Remark2: When several sequences are found inside a FASTA file,
they are considered as different sequences and processed to build the Markov model.
If the FASTA file contains a sequence split into contigs, thus needing
to be concatenated, then a preprocessing of the file is required to remove the title
lines before it can be passed as an argument to BuildMarkov.



Next: The GRAMMAR package: Context-Free
Up: GenRGenS v2.0 User Manual
Previous: Generalities and file formats
Contents
Yann Ponty
2007-04-19