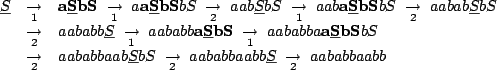


Next: The RATIONAL package :
Up: GenRGenS v2.0 User Manual
Previous: The MARKOV package :
Contents
Subsections
For many years, the context free grammars have been used in the theoretical languages field
They seem to be the best compromise between computability and expressivity. Applied to genomics,
they can model long range interactions, such as base pairings inside an RNA, as shown by D.B. Searls[12]. We provide in this
package generation algorithms for two classes of models based on Context Free Grammars: the uniform models and
the weighted models. In the former, each sequence of a given size has the same probability of being drawn. In the
latter, each sequence's probability is proportional to its composition.
Like stochastic grammars, a weight set can be guessed to achieve specific frequencies. Unlike stochastic grammars,
one can control precisely the size of the output sequences.
The term context-free for our grammars equals to a restriction over the form of the rules. This restriction is
based on language theoretical properties.
A sample of context-free grammar, and the way a sequence is produced from the axiom can be seen in figures 4.1
and 4.2.
Figure 4.1:
A context free grammar for the well-balanced words
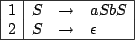 |
Figure 4.2:
Derivation of the word
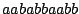 from the axiom
from the axiom  .
.
 are the freshly produced letters.
are the freshly produced letters.
 are the letters that will be rewritten at next step.
are the letters that will be rewritten at next step.
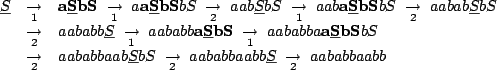 |
In the computer science and combinatorics fields, words issued from grammars are used as codes
for certain objects, like computer programs, combinatorial objects, ...For instance, the grammar
whose rules are given in figure 4.1 naturally encodes well balanced parenthesis words, if 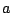 stands for a
opening parenthesis and
stands for a
opening parenthesis and 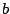 stands for a closing one . A one to one correspondence has also
been shown between the words generated by this grammar and some classes of trees. As trees are also
used as approximations of biological structures, it is possible to consider the use of context-free grammars as discrete
models for genomic structures.
stands for a closing one . A one to one correspondence has also
been shown between the words generated by this grammar and some classes of trees. As trees are also
used as approximations of biological structures, it is possible to consider the use of context-free grammars as discrete
models for genomic structures.
We now discuss the utility of context-free grammars as discrete models for genomic structures. Most of the commonly-used
models do only take into account a smallest subset of their neighborhood. For instance, in a Markov model, the probability
of emission of a letter depends only on a fixed number of previously emitted letters. Although these models can prove
sufficient when structural data can be neglected, they fail to capture the long-range interaction in structured
macromolecules such that RNAs or Proteins. Back to our CFGs, figure 4.2 illustrates the fact that letters
produced at the same step can at the end of the generation be separated by further derivations. As we claim that dependencies
inside a CFG-based model rely on some terminal symbols proximity inside of the rules, CFGs can capture both
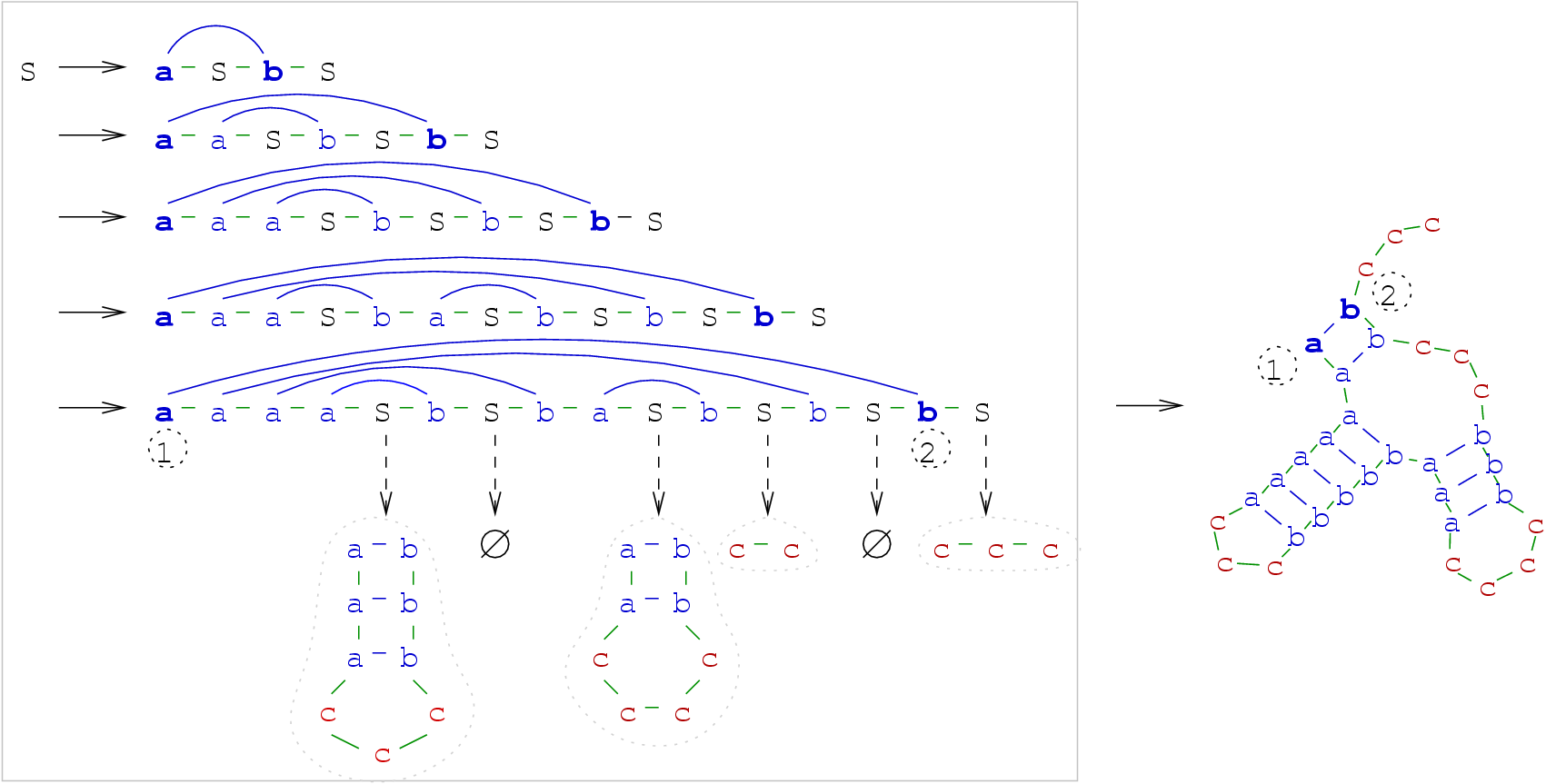
sequential and structural properties, as illustrated by figure 4.3.
Figure 4.3:
Long range interaction between bases 1 and 2 can be captured by CFGs, as they are generated at the same stage,
and then separated by further non-terminal expansions. The CFG used here is an enrichment of the one shown in Figure 4.2
|
|
The uniform random generation algorithm, adapted from a more general one[8], is briefly described here.
At first, we motivate the need for a precomputation stage, by pointing
out the fact that a stochastic approach is not sufficient to achieve uniform generation. Moreover, controlling the size
of the output using stochastic grammar is already a challenge in itself.
To illustrate this point, we introduce the historical grammar for RNA structures, whose rules are described
in figure 4.4.
Figure 4.4:
A CFG grammar for the RNA Secondary Structures
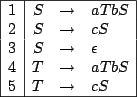 |
Now, suppose one wants to generate a word of size 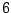 uniformly at random from this grammar.
A natural idea would be to rewrite from the axiom
uniformly at random from this grammar.
A natural idea would be to rewrite from the axiom  until a word of size
until a word of size 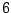 is obtained.
Therefore, you have to check wether each derivation yields a word of the desired length, as,
for instance, the
is obtained.
Therefore, you have to check wether each derivation yields a word of the desired length, as,
for instance, the
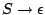 rule produces only the empty word and needs not
to be investigated.
rule produces only the empty word and needs not
to be investigated.
Once you have built a set of derivations suitable for a given length, you have to carefully
associate probabilities with each derivation. Indeed, choosing any of the eligible 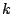 rules with
probability
rules with
probability 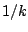 may end in a biased generation, as the numbers of sequences accessible from
any rules are not equal. This fact is illustrated by the example from figure 4.4,
where the two eligible rules for sequences of size
may end in a biased generation, as the numbers of sequences accessible from
any rules are not equal. This fact is illustrated by the example from figure 4.4,
where the two eligible rules for sequences of size 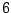 from the axiom
from the axiom 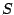 are
are
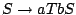 (1) and
(1) and
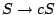 (2).
(2).
Figure 4.5:
Deriving words of size 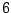 from
from 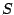
|
|
As illustrated by figure4.5,
choosing rules (1) or (2) with equal probabilities is equivalent to grant the set of words
produced by rules (1) and (2) with total probabilities 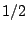 and
and 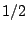 . As these sets do not
have equal cardinalities, uniform random generation cannot be achieved.
That is why the grammar is first analyzed during a preprocessing stage, that precomputes the
probabilities of choosing rules at any stage of the generation. These probabilities are proportional
to the number of sequences accessible after the choice of each applicable rule for a given non-terminal,
normalized by the total number of sequence for this non-terminal.
. As these sets do not
have equal cardinalities, uniform random generation cannot be achieved.
That is why the grammar is first analyzed during a preprocessing stage, that precomputes the
probabilities of choosing rules at any stage of the generation. These probabilities are proportional
to the number of sequences accessible after the choice of each applicable rule for a given non-terminal,
normalized by the total number of sequence for this non-terminal.
Once these computations are made, it is possible to perform uniform random generation by choosing a
rewriting using the precomputed probabilities, as shown in figure 4.6.
Figure 4.6:
The complete tree of probabilities for the words of size 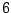 .
.
|
|
Weighted languages for controlled non-uniform random generation
Although uniform models can prove useful in the analysis of algorithms, or to shed the light on some overrepresented phenomena,
they are not always sufficient to model biological sequences or structures. For instance, it can be shown using combinatorial tools that
the classical model for RNA secondary structures from figure 4.4 produces on the average
one base-pair-long helices (see [10] or [11]), which is not realistic.
Furthermore, substituting the rule 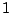 with
a rule
with
a rule
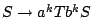 in order to constrain the minimal number of base pairs inside an helix only raises
the average length of an helix to exactly
in order to constrain the minimal number of base pairs inside an helix only raises
the average length of an helix to exactly 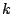 , loosing all variability during the process.
, loosing all variability during the process.
Thus, we proposes in [5] a way to control the values of the parameters of interest by putting weights
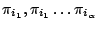 on the terminal letters
on the terminal letters
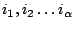 . We then define the weight of a sequence to be the product of the individual weights
of its letters. For instance, in a weighted CFG model having weights
. We then define the weight of a sequence to be the product of the individual weights
of its letters. For instance, in a weighted CFG model having weights 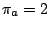 ,
, 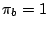 and
and 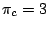 , a sequence
, a sequence
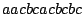 has a weight of
has a weight of
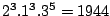 .
.
By making a few adjustments during the precomputation stage, it is possible to constrain
the probability of emission of a sequence to be equal to its weight, normalized by the sum of weights of all sequences of the same size.
Under certain hypothesis, it can be proved that for any expected frequencies for the terminal
letters, there exists weights such that the desired frequencies are observed. By assigning heavy weights
to the nucleotides inside helices, and low ones to helices starts, it is now possible to control the
average size of helices, terminal loops, bulges and multiloops.
To illustrate the effect of such weightings, we consider the previous example from figure 4.5, and we point the fact that the
average number of unpaired bases equals to
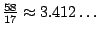 in the uniform model. By assigning a weight
in the uniform model. By assigning a weight
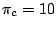 to each unpaired base
letter, we obtain the probabilities of emission for sequences of size
to each unpaired base
letter, we obtain the probabilities of emission for sequences of size 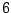 summarized in table 4.7.
summarized in table 4.7.
Figure 4.7:
Probabilities for all words of size 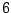 under
under
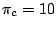
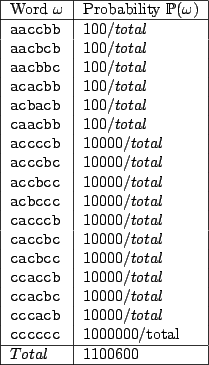 |
These probabilities yield a new expectancy for the number of unpaired bases in a random structure of
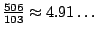 .
So, by assigning a weight barely higher than
.
So, by assigning a weight barely higher than 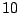 (
(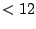 ), it is possible to constrain the average number of the unpaired base symbol
c to be
), it is possible to constrain the average number of the unpaired base symbol
c to be 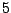 out of
out of 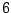 . This property holds only for sequences of size
. This property holds only for sequences of size 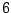 , but another weight can be computed for any
sequence size. Moreover, we claim that, under certain common sense hypothesis, the frequency of a given symbol quickly reaches an
asymptotic behaviour, so that the weight do not need to be adapted to the sequence size above a certain point.
This section describes the syntax and semantics of context-free grammar based description files.
, but another weight can be computed for any
sequence size. Moreover, we claim that, under certain common sense hypothesis, the frequency of a given symbol quickly reaches an
asymptotic behaviour, so that the weight do not need to be adapted to the sequence size above a certain point.
This section describes the syntax and semantics of context-free grammar based description files.
Figure 4.8:
Main structure of a context-free grammar description file
![\begin{figure}
\begin{center}
\texttt{\begin{tabular}{l}
TYPE = GRAMMAR \\...
...] \\ [0.1cm]
[ALIASES = ...]
\end{tabular}}
\end{center}
\end{figure}](img149.gif) |
Clauses nested inside square brackets are optional. The given order for the clauses is mandatory.
Context-free grammar based description files define some attributes and properties of the grammar.
SYMBOLS = {WORDS,LETTERS}
Optional, defaults to SYMBOLS = WORDS
Chooses the type of symbols to be used for random generation.
When WORDS is selected, each pair of symbols must be separated by at least a blank character (space, tabulation or newline).
This affects mostly the RULES clause, where the right-hand-sides of the rules will be made of words, separated by blank
characters. This feature can greatly improve the readability of the description file as shown in the example from figure 4.9.
Figure 4.9:
The skeleton of a grammar for the tRNA
 |
A LETTERS value for the SYMBOLS parameter will force GenRGenS to see a word as sequence of symbols. For instance,
the right hand side of the rule S->aSbS will decompose into S -> a S b S if this option is invoked. Moreover,
blank characters will be inserted between symbols in the output.
START = 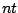
Optional, defaults to START = 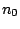 , with
, with 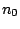 being the left hand side of the first
rule defined by the RULES clause.
being the left hand side of the first
rule defined by the RULES clause.
Defines the axiom 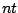 of the grammar, that is the non-terminal letter initiating the generation. This letter
must of course be the left-hand-side of some rule inside the RULES clause below.
Required
of the grammar, that is the non-terminal letter initiating the generation. This letter
must of course be the left-hand-side of some rule inside the RULES clause below.
Required
Defines the rules of the grammar.
Rules are composed of letters, also called symbols. Each symbol 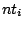 that appears as the left-hand side of a rule becomes
a non-terminal symbol, that is a symbol that needs further rewriting.
that appears as the left-hand side of a rule becomes
a non-terminal symbol, that is a symbol that needs further rewriting. 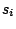 are sequences of symbols that can weither appear
or not as the left-hand side of rules, separated by spaces or tabs if SYMBOLS=LETTERS is selected.
are sequences of symbols that can weither appear
or not as the left-hand side of rules, separated by spaces or tabs if SYMBOLS=LETTERS is selected.
If the START clause is omitted, the axiom for the grammar will be 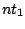 .
.
The characters ::= can be used instead of -> to separate the left-hand side
symbols from the right-hand side ones.
Optional, weights default to 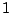 .
.
Defines the weights of the terminal letters 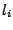 .
.
As discussed in section 4.3, assigning a weight 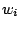 to a terminal letter
to a terminal letter 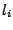 is a way
to gain control over the average frequency of
is a way
to gain control over the average frequency of 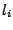 . For instance, in a grammar over the alphabet
. For instance, in a grammar over the alphabet
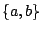 , adding a clause WEIGHTS = a 2 will grant sequences aaab and bbbb with
weights
, adding a clause WEIGHTS = a 2 will grant sequences aaab and bbbb with
weights 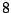 and
and 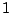 , i.e. the generation probability of aaab will be
, i.e. the generation probability of aaab will be 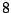 times higher than that of
bbbb.
The following description file captures some structural properties of the tRNA.
times higher than that of
bbbb.
The following description file captures some structural properties of the tRNA.
Figure 4.10:
A basic CFG-based model for the tRNA
 |
In 1, we choose a context free grammar-based model.
In 2, we use words, a reader-friendly choice for such a complicated(though still a little simplistic) model.
In 3, we choose the non-terminal symbol tRNA as our starting symbol. Every generated sequence will
be obtained from iterative rewritings of this symbol. Here, this clause has no real effect, as the default behaviour of
GenRGenS is to choose the first non-terminal to appear in a rule as the starting symbol.
Clause 4 describes the set of rules. The correspondance between non-terminal symbols an substructures
is detailled in figure 4.11.
Figure 4.11:
Non-terminal symbols and substructures
|
|
Note that we use different alphabets to discern paired bases from unpaired ones, which allows discrimination
of unpaired bases using weights in clause 5.
Of course, it is possible to get a more realistic model by substituting the X_Loop -> Fill rules with
specific set of rules, using different alphabets. Thus, one would be able to control the size and composition of each
loop.
In 5, we discriminate the unpaired bases, which increases size of the helices. Indeed, uniformity tends to favor
very small if not empty helices whereas the weighting scheme from this clause penalizes so much the occurences of unpaired
bases that the generated structures now have very small loops.
In 6, the sequence's alphabet is unified by removing traces of the structure.
During the precomputation stage, GenRGenS uses arbitrary precision arithmetics to handle numbers that can grow over
the size in an exponential way. However, for special languages or small sequences, it is possible to avoid using
time-consumming arithmetics, and to limit the computation to double variables. This is the purpose of the
-f option. The -s option toggles on and off the computation and display of
frequencies of symbols for each generated sequence.
Grammar specific command line options usage:
java -cp . GenRGenS.GenRGenS -size n -nb k -f [T F] -s [T
F] -s [T F] GrammarGGDFile
F] GrammarGGDFile
- -f [T
 F]: Activates/deactivates the use of light and limited double variables instead of
heavier but more accurate BigInteger ones. Misuse of this option may result in division by zero or non-uniform generation.
Defaults to -f F.
F]: Activates/deactivates the use of light and limited double variables instead of
heavier but more accurate BigInteger ones. Misuse of this option may result in division by zero or non-uniform generation.
Defaults to -f F.
- -s [T
 F]: Enables/disables statistics about each sequence.
Defaults to -s F.
F]: Enables/disables statistics about each sequence.
Defaults to -s F.



Next: The RATIONAL package :
Up: GenRGenS v2.0 User Manual
Previous: The MARKOV package :
Contents
Yann Ponty
2007-04-19