


Next: The MASTER package :
Up: GenRGenS v2.0 User Manual
Previous: The GRAMMAR package: Context-Free
Contents
Subsections
At the bottom of Chomsky's formal languages hierarchy lies the regular expressions. Taken as languages theory tools, their main
purpose is the description of subsets over the whole set of sequences that can be parsed and/or generated by very simple machines called
finite state automata over finite alphabets. This class is known to be a subclass of the one that is implemented by the
context-free grammar, but more efficient random generation algorithms are available for it.
Because of their simplicity, they have been extensively used to model families of genomic sequences
differing only on a few positions. In the Prosite database, which is well known database of protein families and domains, a pattern
(or consensus) is built from a given set of sequences, sharing functional properties. These so-called Prosite patterns are related
to regular expressions, as shown in 5.1.3.
GenRGenS provides a random generation process both for Prosite patterns and regular expressions.
For instance, random sequences drawn with respect to a Prosite pattern supposedly being a fingerprint for a biological
property can be used to test its relevance. One can also generate simple mutants from a regular expression by introducing
some choice places inside the sequence. Such sequences can used for computation of statistical scores, such as Z-Scores, and P-values.
In this chapter, we will describe the syntax and semantics of the regular expressions. We will then explain
how GenRGenS turns a ProSite pattern into a regular expression associated with the same language, and show how
uniform random generation can be performed from a regular expression.
Regular expressions syntax
A regular expression 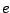 is a language description tool, recursively defined as follows :
Where
is a language description tool, recursively defined as follows :
Where 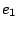 and
and 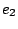 are regular expressions, and
are regular expressions, and 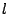 stands for any letter among the alphabet.
stands for any letter among the alphabet.
The
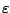 is a shortcut for an empty word(a word of size 0).
is a shortcut for an empty word(a word of size 0).
Formally, a language can be seen as a set of words over a given alphabet.
The meanings of these alternatives are related to the languages denoted by such expressions.
- -
- The disjonction
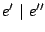 : The language is the union of the languages associated to
: The language is the union of the languages associated to 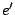 and
and 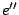 . Any word of
. Any word of
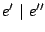 belongs
to
belongs
to 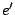 or
or 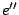 .
.
- -
- The concatenation
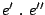 : The language is the concatenation of the languages associated to
: The language is the concatenation of the languages associated to 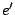 and
and 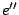 . Any word among
. Any word among
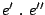 can be decomposed into a concatenation of words issued from
can be decomposed into a concatenation of words issued from 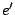 and
and 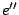 .
.
- -
- The iteration
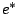 : Each word of the resulting language is a concatenation of a finite set of words issued from
: Each word of the resulting language is a concatenation of a finite set of words issued from 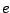 .
.
- -
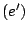 : The language is that of
: The language is that of 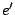 . This construction is useful to avoid ambiguity. For instance, the expression
. This construction is useful to avoid ambiguity. For instance, the expression 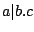 can denote the language
can denote the language 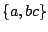 or the language
or the language 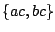 .
.
- -
-
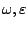 : The only word among the language is the single character
: The only word among the language is the single character 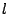 , resp.
, resp.
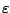 .
.
Example 1:
The regular expression 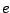 describes a simplistic model for an ORF, that is a subsequence of a DNA code starting
with a START base triplet
describes a simplistic model for an ORF, that is a subsequence of a DNA code starting
with a START base triplet 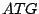 and ending with one of the STOP base triplets TAG/TGA/TAA.
It should be noticed that anything can happen between the START and STOP codon, as the
and ending with one of the STOP base triplets TAG/TGA/TAA.
It should be noticed that anything can happen between the START and STOP codon, as the
 part of
part of 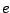 doesn't excludes STOP base triplets.
doesn't excludes STOP base triplets.
Example 2:
Such expressions are also perfectly fit to model mutants. Suppose you're given three 5.8S ribosomal RNA sequences close one to another and
aligned as follows.
| ... |
C |
G |
C |
C |
C |
C |
G |
C |
C |
G |
G |
C |
G |
G |
... |
| ... |
A |
C |
G |
C |
G |
A |
C |
C |
C |
G |
G |
U |
G |
G |
... |
| ... |
C |
C |
U |
G |
U |
U |
. |
G |
U |
G |
G |
U |
G |
G |
... |
A regular expression 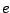 can then be used to model a family of sequences that contains the three original sequences, among with some
other sequences close to the originals.
PROSITE is a database of protein families and domains.It consists of biologically significant sites, patterns and
profiles that help to identify to which known protein family a new sequence belongs. It was started in 1989 by Amos
Bairoch, and is part of the SWISS-PROT program[2]. It features text-files structured by tags and carriage-returns.
Among these tags, some are used to define patterns to model sequential aspects behind functional properties.
They can be seen as consensus, as they capture some sequential
similarities of a given entry set of sequences.
can then be used to model a family of sequences that contains the three original sequences, among with some
other sequences close to the originals.
PROSITE is a database of protein families and domains.It consists of biologically significant sites, patterns and
profiles that help to identify to which known protein family a new sequence belongs. It was started in 1989 by Amos
Bairoch, and is part of the SWISS-PROT program[2]. It features text-files structured by tags and carriage-returns.
Among these tags, some are used to define patterns to model sequential aspects behind functional properties.
They can be seen as consensus, as they capture some sequential
similarities of a given entry set of sequences.
Further informations can be found at:
http://www.expasy.org/prosite/prosuser.html
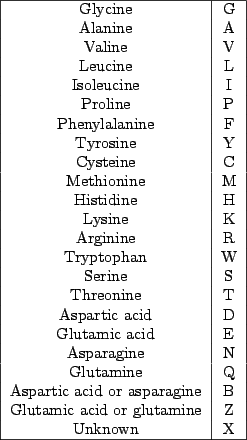
Let
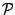 be the set of all known amino-acids, abbreviated with respect to the standard
one-letter IUPAC code5.1
given by figure 5.1.2.2.
be the set of all known amino-acids, abbreviated with respect to the standard
one-letter IUPAC code5.1
given by figure 5.1.2.2.
Figure 5.1:
Standard codes for the amino-acids, as proposed by the IUPAC
 |
Then a PROSITE pattern 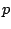 can then be recursively defined as follows:
where
can then be recursively defined as follows:
where 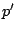 and
and 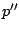 are PROSITE patterns;
are PROSITE patterns; 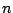 ,
, 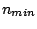 and
and 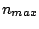 are positive integers;
are positive integers; 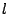 is a sequence of amino-acids encoded
with respect to the IUPAC code for the amino-acids. The semantics for the preceeding alternatives is described below :
is a sequence of amino-acids encoded
with respect to the IUPAC code for the amino-acids. The semantics for the preceeding alternatives is described below :
- -
- The concatenation
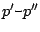 : protein codes are derived from patterns
: protein codes are derived from patterns 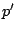 and
and 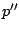 and concatenated.
and concatenated.
- -
- The strict iteration
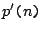 : a protein code is derived from pattern
: a protein code is derived from pattern 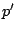 and copied
and copied 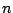 times.
times.
- -
- The loose iteration
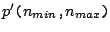 : a protein code is derived from pattern
: a protein code is derived from pattern
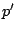 and copied from
and copied from 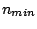 to
to 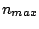 times.
times.
- -
- The identity
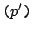 : This notation is equivalent to
: This notation is equivalent to 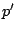 , and simply means that a sequence is issued
from
, and simply means that a sequence is issued
from 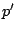 . It can be used to resolve some ambiguities.
. It can be used to resolve some ambiguities.
- -
- The inclusive disjonction
![$ \texttt{[}l\texttt{]}$](img198.gif) : Any amino-acid code can be choosed from the list
: Any amino-acid code can be choosed from the list 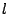 .
.
- -
- The exclusive disjonction
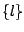 : Any amino-acid code that is not in the list
: Any amino-acid code that is not in the list 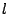 can be choosed.
can be choosed.
- -
- The wildcard
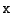 : Any amino-acid, including the unknown
: Any amino-acid, including the unknown 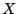 code.
code.
- -
- The amino-acid sequence
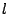 :
: 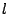 is a word composed of amino-acid codes.
is a word composed of amino-acid codes.
As the rational expressions are also defined using concatenations, iterations and disjunctions, a PROSITE pattern can be considered
as a rational expression. The correspondance between PROSITE elementary operations and rational ones are listed below:
Its is a classical result of the formal language theory that any regular expression can be
turned into an automaton that recognises/generates the same language. Such an automaton can be turned into
a deterministic one, that is an automaton where each accepted word is uniquely coupled with a walk between two
special states (start and final). Thus, instead of expanding a initial non-terminal symbol the way we did for
the GRAMMAR package, we are going to walk inside of this automaton with carefuly chosed probabilities.
For instance, consider the ORFs inside of DNA. They start with a START codon ATG, then follows a region of
codons that are not STOP-ones, and finally they end with the STOP codon TAA.
This can be modelled by the following expression, whose deterministic automaton is shown in figure 5.2.
Figure 5.2:
Deterministic automaton corresponding to the simple ORF model.
|
|
Each sequence is bijectively associated with a single path in the resulting. For instance, the sequence ATG AAT TCG GAT TAA
corresponds to the state sequence 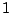 -
-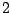 -
-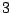
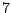 -
-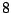 -
-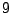
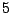 -
-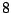 -
-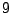
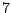 -
-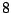 -
-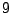
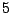 -
-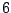 -
-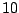 . As explained in the GRAMMAR package, the choice of the
next state must be made using correct probabilities in order to achieve
uniformity. These probabilities are proportional to the amount of words
reachable from the destination state. Once again these numbers can be
computed using simple linear recurrences before the generation stage.
. As explained in the GRAMMAR package, the choice of the
next state must be made using correct probabilities in order to achieve
uniformity. These probabilities are proportional to the amount of words
reachable from the destination state. Once again these numbers can be
computed using simple linear recurrences before the generation stage.
Controlled non-uniform random generation can also be achieved using the
same distributions as within the GRAMMAR package. Indeed, each
symbol(letter, IUPAC Code) can be associated with a weight inside the
WEIGHT clause, so that a sequence's probability will the product
of all its letters' weights, normalized by the sum of all the weights over
the sequence set denoted by the expression. This weight mechanism may be used for
instance to increase the proportion of a given base as well as to favor the
occurence of a given structured motif.
The main structure of the file is shown in figure 5.3
Figure 5.3:
Main structure of a RATIONAL description file
![\begin{figure}
\begin{center}
\texttt{\begin{tabular}{l}
TYPE = RATIONAL \...
.....\\ [0.1cm]
[ALIASES = ...]
\end{tabular}}
\end{center}
\end{figure}](img207.gif) |
LANGUAGE = RATIONAL | PROSITE
Required
Chooses between rational/regular expression and PROSITE pattern syntaxes for the expression.
EXPRESSION = 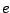
Required
The rational or PROSITE expression. The syntax for 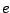 depends on the value of the LANGUAGE clause,
and has always been described in section 5.1.1 for a RATIONAL choice, and in section
5.1.2.2 for PROSITE patterns.
Optional, all weights default to
depends on the value of the LANGUAGE clause,
and has always been described in section 5.1.1 for a RATIONAL choice, and in section
5.1.2.2 for PROSITE patterns.
Optional, all weights default to 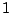 .
.
Defines the weights of the terminal letters 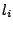 .
.
As discussed in section 4.3 for the GRAMMAR description file, assigning a weight 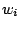 to a terminal letter
to a terminal letter 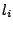 is a way to gain control over the average frequency of
is a way to gain control over the average frequency of 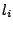 .
We show and explain the GenRGenS description file corresponding to the simple ORF model shown in
figure 5.2.
On line 1, we choose the RATIONAL package for random generation.
.
We show and explain the GenRGenS description file corresponding to the simple ORF model shown in
figure 5.2.
On line 1, we choose the RATIONAL package for random generation.
On line 2, we select a rational/regular expression.
On line 3, the rational expression corresponding to the simple ORF model from figure
5.2. Notice that the star operator * has highest precedence,
so that "A|B*"
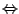 "A|(B*)"
"A|(B*)"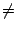 "(A|B)*".
On lines 4 and 5, weights are assigned to the C's and G's. A weight higher than
"(A|B)*".
On lines 4 and 5, weights are assigned to the C's and G's. A weight higher than 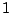 for a symbol
will increase its number of occurence within generated sequences. Here, we choose to favor C and G
among the coding area.
for a symbol
will increase its number of occurence within generated sequences. Here, we choose to favor C and G
among the coding area.
On lines 6 and 7, the symbols C' and G' were only introduced to allow the assignment of
weights within the coding area. Indeed, we needed the weight not to affect the G from the START codon.
We don't really need them anymore, so we send them back to their original representations C and G.
We illustrate the use of GenRGenS' RATIONAL package to generate protein sequences with respect
to a given PROSITE pattern by a real-life example. The pattern CBM1_1 can be found under
accession code PS00562 on expasy's and is considered as a signature for the carbohydrate
binding type-1 domain. Figure 5.4 shows its entry in the PROSITE database.
Figure 5.4:
PROSITE entry for pattern CBM1_1
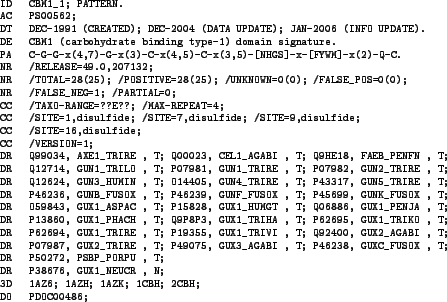 |
The PA line of the PROSITE file can be inserted directly into the
EXPRESSION clause, without the terminal dot, resulting
in the following description file:
On line 1, we choose the RATIONAL package for random generation.
On line 2, we select a PROSITE pattern expression.
On line 3 and 4, the PROSITE pattern.
The default behaviour of GenRGenS is to generate sequences of the size provided through the -size command line option.
However, it can also be useful to generate among every words possibly drawn from a PROSITE expression, regardless of the size.
This is the purpose of the -i option. The sequences are still drawn at random.
Rational specific command line options usage:
java -cp . GenRGenS.GenRGenS -size n -nb k -i [T F] PrositeGGDFile
F] PrositeGGDFile
- -i [T
 F]:When T is selected, ignores the size parameter, so that the sequences
are drawn at random among the finite set corresponding to the PROSITE pattern defined in the file
PrositeGGDFile. Generates sequences of the given size otherwise.
F]:When T is selected, ignores the size parameter, so that the sequences
are drawn at random among the finite set corresponding to the PROSITE pattern defined in the file
PrositeGGDFile. Generates sequences of the given size otherwise.
Defaults to -i F.



Next: The MASTER package :
Up: GenRGenS v2.0 User Manual
Previous: The GRAMMAR package: Context-Free
Contents
Yann Ponty
2007-04-19
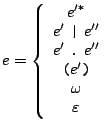
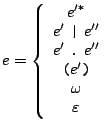
![$\displaystyle p = \left\{ \begin{array}{c}
p'\texttt{-}p''\\
p'\texttt{(}n\...
...exttt{]}\\
\texttt{\{}l\texttt{\}}\\
\texttt{x} \\
l \end{array} \right. $](img189.gif)


![\begin{figure}
\begin{center}
\texttt{\begin{tabular}{\vert c\vert l\vert} \...
...[NHGS]-x-[FYWM]-x(2)-Q-C\\ \hline
\end{tabular}}
\end{center}
\end{figure}](img212.gif)