Eléments de logique pour l’informatique 2021–22
Annexe A Correction des exercices du cours
A.1 Exercices du chapitre 1
Exercice 1
-
∀ x, (joue(self,x)⇒ ami(self,x))
- ∀ x, ∃ y, ami(x,y)
- ¬ (∃ x, (joue(self,x) ∧ ami(self,x))) ou de manière équivalente
∀ x, ((¬ joue(self,x)) ∨ (¬ ami(self,x))
- ∃ x y, (joue(self,x) ∧ joue(self,y)∧ ¬(x=y)) sans la mention de x≠y la formule est vraie dès qu’il existe une personne avec qui je joue.
Exercice 2
∀ x y, ((pair(x)∧ pair(y))⇒ pair(x+y))
Exercice 3
-
∀ x∈ℕ,P correspond à ∀ x,(N(x)⇒ P)
- ∃ x∈ℕ,P correspond à ∃ x,(N(x)∧ P)
Exercice 4
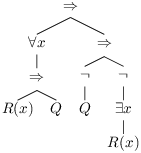
La formule parenthésée est (∀ x, (R(x) ⇒ Q)) ⇒ ((¬ Q) ⇒ (¬ (∃ x, R(x)))) et sous forme d’arbre :
Exercice 5
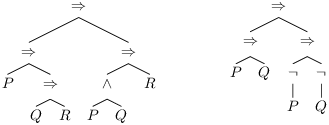
Les formules parenthésées sont (P ⇒ (Q ⇒ R)) ⇒ ((P ∧ Q) ⇒ R) et
(P ⇒ Q) ⇒ ((¬ Q) ⇒ (¬ P))
et sous forme d’arbre
Exercice 6
-
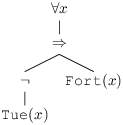
∀ x, ¬ Tue(x) ⇒ Fort(x) correspond au minimum de parenthèses
- ∀ x, ((¬ Tue(x)) ⇒ Fort(x)) correspond à la formule complètement parenthésée
- La forme arborescente est
Exercice 7
La seule variable libre de la formule : ∀ b, b > 0 ⇒
∃ q, ∃ r, a = b × q + r ∧ r < b est la variable a.
Exercice 8
-
La formule ((P ⇒ Q) ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors P ⇒ Q est vrai et donc (P ⇒ Q) ⇒ P est faux et donc ((P ⇒ Q) ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
- La formule (¬ P ⇒ P) ⇒ P est valide. En effet soit P est vrai et elle est vraie. Soit P est faux, mais alors ¬ P est vrai et donc ¬ P ⇒ P est faux et donc (¬ P ⇒ P) ⇒ P est vrai. Dans toutes les interprétations possibles, la formule est vraie. Donc elle est valide.
Exercice 9
-
L’inscription sur la porte 1 correspond à la formule A1 =def P1 ∧ ¬ P2,
- L’inscription sur la porte 2 correspond à la formule A2≡ (P1 ∧ ¬ P2)∨ (P2 ∧ ¬ P1),
- Une seule de ces inscriptions est vraie donc la formule (A1∧ ¬ A2) ∨ (A2∧ ¬ A1) est vraie.
On peut faire une table de vérité de cette dernière formule en fonction des valeurs de P1 et P2 et chercher dans quels cas elle est vraie.
On peut aussi raisonner directement.
Comme A2 est de la forme A1 ∨ B, si A1 est vrai alors A2 est vrai et donc la troisième formule est fausse.
Donc A1 est faux et A2 est vrai et on a P2 ∧ ¬ P1 donc il faut ouvrir la deuxième porte.
Exercice 10
La formule (∀ x, P(x)) ⇒ ∃ x, P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ∀ x, P(x). L’interprétation de P est vraie pour toutes les valeurs dans le domaine D. Comme le domaine est non vide, on peut choisir d∈ D. L’interprétation de P est vraie pour d et donc ∃ x, P(x) est vraie dans cette interprétation.
La formule ¬(∀ x, P(x)) ⇒ ∃ x, ¬ P(x) est vraie quelle que soit l’interprétation de P. En effet si on se donne une interprétation I sur une domaine D, qui rend vraie ¬(∀ x, P(x)). Cette interprétation rend faux ∀ x, P(x) ce qui veut dire qu’il existe d∈ D pour lequel l’interprétation P est fausse et donc l’interprétation de ∃ x, ¬ P(x) est vraie.
Exercice 11
t ≤ u =def ∃ n,
n+t=u.
-
∀ x, 0 ≤ x se réécrit en ∀ x, ∃ n, n+0=x. Soit x quelconque, on choisit pour n la valeur x. Il faut alors montrer x+0=x qui est l’axiome 4 de la théorie arithmétique.
- ∀ x y, x ≤ y ⇔ S(x) ≤ S(y) se réécrit en
∀ x y, (∃ n, n+x=y) ⇔ (∃ n, n+S(x)=S(y)). Soit x et y quelconques, on montre les deux côtés de l’équivalence.
Si ∃ n, n+x=y, soit n tel que n+x=y, on a S(n+x)=S(y) (propriété de la théorie de l’égalité). On en déduit n+S(x)=S(y) (axiome 5 de l’arithmétique) et donc ∃ n, n+S(x)=S(y).
Réciproquement si ∃ n, n+S(x)=S(y), soit n tel que n+S(x)=S(y), on en déduit S(n+x)=S(y) (axiome 5 de l’arithmétique). On en déduit n+x=y (axiome 3 de l’arithmétique) et donc ∃ n, n+x=y.
- transitivité : ∀ x y z, x ≤ y ⇒ y ≤ z ⇒
x ≤ z se réécrit en (∃ n, n+x=y)⇒ (∃ m, m+y=z) ⇒ (∃ p, p+x=z).
Soit x,y et z quelconques, on suppose ∃ n, n+x=y et ∃ m, m+y=z vrai et donc soit n et m tels que n+x=y et m+y=z. Par la théorie de l’égalité, on a m+(n+x)=m+y et par la transitivité de l’égalité on en déduit m+(n+x)=z. L’associativité de l’addition (non démontrée) permet d’en déduire que (m+n)+x=z
et donc ∃ p, p+x=z ce qui conclut la preuve.
Exercice 12
Les définitions utilisent la notion d’ordre strict t<u qui peut se définir par ∃ n,
S(n+t)=u.
-
Le fait que r est le résultat de la division entière
de x par y peut se représenter par la formule
∃ r, x = d× y +r ∧ r < y.
- Le fait que
r est le reste modulo de la division entière de x
par y peut se représenter par la formule ∃
d, x = d× y + r ∧ r < y.
- Si on remplace y par 0 dans la définition de divisibilité, on obtient la formule
∃ r, x = d× 0 +r ∧ r < 0 qui se développe en ∃ r, x = d× 0 +r ∧ (∃ n, S(n+r) = 0) formule qui est toujours fausse si on se place dans un monde qui satisfait les axiomes de la théorie arithmétique et en particulier ∀ x, S(x)≠0.
- Pour représenter le résultat de la division de a par b à l’aide d’un prédicat à trois arguments, il suffit d’introduire une nouvelle variable d et d’utiliser la formule div(a,b,d).
Dans le cas de (x/y)/z=x/(y× z), ill y a trois opérations de division, on introduit donc trois nouvelles variables d1, d2 et d3. d1 est le résultat de la division de x par y, ce qui se traduit par
div(x,y,d1), d2 est le résultat de la division de x/y (c’est-à-dire d1) par z ce qui se traduit par
div(d1,z,d2), finalement d3 est le résultat de la division de x par y× z ce qui se traduit par
div(x,y× z,d3).
Il suffit alors d’exprimer que sous ses hypothèses on a d2=d3. Ce qui s’écrit
| ∀ d1 d2 d3, div(x,y,d1)∧ div(d1,z,d2)∧ div(x,y× z,d3)⇒ d2=d3 |
Il est possible de montrer que la relation div est fonctionnelle c’est-à-dire que div(x,y,d1)∧ div(x,y,d2)⇒ d1=d2, la formule précédente peut donc se simplifier en | ∀ d1 d2, div(x,y,d1)∧ div(d1,z,d2)⇒ div(x,y× z,d2) |
Exercice 13
Il est nécessaire en plus du prédicat pos(i,j,k) qui exprime que le chiffre k est sur la case (i,j) de disposer du prédicat d’égalité pour pouvoir dire qu’un chiffre apparait au plus une fois.
-
Au plus un seul chiffre k par case (i,j): ∀ i j k, pos(i,j,k) ⇒ ∀ l, ¬ l=k⇒ ¬ pos(i,j,l)
- Chaque chiffre k apparaît sur chaque ligne i au moins dans une colonne j:
∀ i k, ∃ j, pos(i,j,k)
- Chaque chiffre k apparaît au plus une fois sur chaque ligne i (s’il est dans la colonne j, il n’est pas dans une autre colonne) :
∀ i j1 j2 k, pos(i,j1,k)∧ pos(i,j2,k)⇒ j1=j2
- Le cas des colonnes est analogue à celui des lignes. On traite ici la notion de carré. Si on veut éviter de traiter chaque valeur de ligne et de colonne individuellement, on peut introduire un symbole de fonction tiers unaire qui, étant donné une ligne ou une colonne, va nous dire dans quel tiers du tableau elle se trouve (premier, deuxième ou troisième). On peut ainsi tester si deux positions (i1,j1) et(i2,j2) seront dans le même carré si et seulement si les indices de ligne sont dans le même tiers du tableau et de même pour les indices de colonnes.
Pour représenter le fait que chaque chiffre k apparaît au plus une fois dans chaque carré on utilisera la formule :
| ∀ i1 i2 j1 j2 k, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2) |
| ⇒ pos(i1,j1,k)∧ pos(i2,j2,k) |
| ⇒ i1=i2∧ j1=j2 |
|
On peut aussi représenter le fait que chaque chiffre apparaitra au moins une fois dans chaque carré de la manière suivante :
| ∀ i1 j1 k, ∃ i2 j2, tiers(i1)=tiers(i2)∧ tiers(j1)=tiers(j2)∧ pos(i2,j2,k) |
Les deux formules sont redondantes dès lors qu’il y a 9 valeurs et 9 cases. En effet, on a écrit qu’il y avait au moins une valeur par case et qu’il ne pouvait pas y avoir deux fois la même valeur, donc chaque valeur va apparaître au moins une fois car une application injective (resp. surjective) d’un ensemble fini dans un ensemble de même cardinal est bijective.
- On exprime dans la logique le fait qu’on a 9 valeurs possibles pour les lignes, les colonnes et les chiffres dans les cases. Cela se fait en ajoutant 9 constantes :1,…,9. Il faut un axiome qui dit que l’univers est formé uniquement de ces 9 éléments
∀ x,x=1∨ …∨ x=9 auquel il faut ajouter les 36 axiomes qui disent que les constantes sont différentes deux à deux ¬1=2,¬1=3,…,¬1=9,¬2=3,…, ¬8=9.
Il faudra aussi ajouter les 9 axiomes qui permettent de raisonner sur la fonction tiers à savoir
tiers(1)=1,tiers(2)=1,tiers(3)=1,…,,tiers(9)=3.
Exercice 14
| nbsymb(p) | =0 si p atomique |
| nbsymb(¬ A) | =1+ nbsymb(A) |
| nbsymb(∀ x, A) | = 1+nbsymb(A) |
| nbsymb(∃ x, A) | = 1+nbsymb(A) |
| |
|
| | nbsymb(A∧ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A∨ B) | =1+ nbsymb(A)+nbsymb(B) |
| nbsymb(A⇒ B) | =1+ nbsymb(A)+nbsymb(B) |
|
Exercice 15
| prof(p) | =0 si p atomique |
| prof(¬ A) | =1+ prof(A) |
| prof(∀ x, A) | = 1+prof(A) |
| prof(∃ x, A) | = 1+prof(A) |
| |
|
| | prof(A∧ B) | =1+ max(prof(A),prof(B)) |
| prof(A∨ B) | =1+ max(prof(A),prof(B)) |
| prof(A⇒ B) | =1+ max(prof(A),prof(B)) |
|
Exercice 16
-
si x ∈ X alors vars(x)={x}
- si c ∈ F0 alors vars(c)=∅
- si f ∈ Fn alors vars(f(t1,…,tn))=
vars(t1)∪…∪ vars(tn)
Exercice 17
On considère ici des termes qui ne contiennent pas de variable
-
définition de feuilles
| feuilles(є)=1 feuilles(N(l,r)) = feuilles(l)+feuilles(r) |
- définition de noeuds
| noeuds(є)=0 noeuds(N(l,r)) = 1+noeuds(l)+noeuds(r) |
- preuve par récurrence que pour tout terme t sans variable, on a feuilles(t)=noeuds(t)+1.
-
cas où t est la constante є on a
feuilles(є)=1 et noeuds(є)=0 d’où le résultat.
- cas où t est de la forme N(l,r) avec l et r deux sous-arbres qui vérifient l’hypothèse de récurrence
feuilles(l)=noeuds(l)+1 et feuilles(r)=noeuds(r)+1.
On a
| feuilles(N(l,r)) | = feuilles(l)+feuilles(r) | définition de feuilles |
| | =noeuds(l)+1+noeuds(r)+1 | hypothèses de récurrence |
| | =noeuds(N(l,r))+1 | définition de noeuds |
|
On en déduit que la propriété est vraie pour tous les arbres.
Exercice 18
La théorie de l’égalité contient les axiomes pour la reflexivité, la symétrie et la transitivité ainsi que des axiomes pour les symboles de fonctions et les prédicats d’arité au moins 1.
Dans le cas de la signature qui est donnée, il y aura donc deux axiomes
-
∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ g(x1,y1)=g(x2,y2)
- ∀ x1 x2 y1 y2, x1=x2∧ y1=y2 ⇒ Q(x1,y1)⇒ Q(x2,y2)
On veut montrer que la formule t=u ⇒ P[x← t]⇒ P[x← u] est valide pour n’importe quelle formule P du langage.
On commence par montrer un cas particulier à savoir que
la formule t=u ⇒ v[x← t]=v[x← u] est valide pour n’importe quel terme v du langage.
On se place dans une interprétation qui rend vraie la formule t=u (et les axiomes de l’égalité) et on utilise une récurrence sur la structure du terme v pour montrer que
v[x← t]=v[x← u] est également vraie dans cette interprétation.
-
si v est une variable z alors soit z=x et la formule devient t=u qui est vraie par hypothèse sur l’interprétation, soit z≠x et la formule devient z=z qui est vraie par reflexivité de l’égalité.
- si v est la constante a alors la formule devient a=a qui est vraie par reflexivité de l’égalité.
- si v est de la forme g(v1,v2) avec v1 et v2 qui vérifient l’hypothèse de récurrence à savoir v1[x← t]=v1[x← u] et v2[x← t]=v2[x← u]. On a g(v1,v2)[x← t]=g(v1[x← t],v2[x← t]), par définition de la substitution. En appliquant les hypothèses de récurrence et l’axiome 1 de l’égalité ci-dessus, on obtient g(v1,v2)[x← t]=g(v1[x← u],v2[x← u]) et donc finalement
g(v1,v2)[x← t]= g(v1,v2)[x← u]
On montre ensuite par récurrence sur la formule P que pour tous les termes t et u et toute interprétation qui rend vraie t=u, on a P[x← t]⇒ P[x← u] est vraie quelque soit l’environnement pour les valeurs des variables libres de P[x← t].
-
Si P est une formule atomique :
Si P est ⊥ ou ⊤ qui ne contient pas x alors il faut montrer P⇒ P qui est une tautologie.
Si P est de la forme Q(v1,v2) alors il faut montrer
Q(v1,v2)[x← t]⇒ Q(v1,v2)[x← u]
Par definition de la substitution, cela revient à montrer
Q(v1[x← t],v2[x← t])⇒ Q(v1[x← u],v2[x← u])
en utilisant l’axiome 2 de la théorie de l’égalité, il suffit de montrer
v1[x← t]=v1[x← u]∧ v2[x← t]=v2[x← u]. Or cette propriété est vraie d’après ce que nous avons établi précédemment.
- Si P est de la forme ¬ A alors il faut montrer (¬ A)[x← t]⇒ (¬ A)[x← u], c’est-à-dire ¬ (A[x← t])⇒ ¬ (A[x← u]) en prenant la contraposée, on est ramené à montrer A[x← u]⇒ A[x← t]. Comme une interprétation qui rend vraie t=u rend aussi vraie u=t par symétrie de l’égalité, on peut appliquer l’hypothèse de récurrence à A avec les termes u et t.
- Si P est de la forme A∘ B avec ∘ l’un des 2 connecteurs propositionnels ∧ ou ∨, alors il faut (A∘ B)[x← t]⇒ (A∘ B)[x← u], c’est-à-dire (A[x← t]∘ B[x← t])⇒ (A[x← u]∘ B[x← u]) or par hypothèse de récurrence on A[x← t]⇒ A[x← u] et B[x← t]⇒ B[x← u]. On conclut en utilisant les propriétés des connecteurs (si A1⇒ A2 et B1⇒ B2 alors A1∧ B1⇒ A2∧ B2 et A1∨ B1⇒ A2∨ B2.
- Si P est de la forme A⇒ B, le raisonnement est presque le même sauf que
la propriéte (A1⇒ B1)⇒ (A2⇒ B2) est une conséquence de A2⇒ A1 et B1⇒ B2. Il faut donc intervertir t et u comme dans le cas de la négation.
- Si P est de la forme ∀ z,A. On choisit la variable liée z pour qu’elle ne soit pas libre ni dans t ni dans u (sinon la substitution n’est pas définie) et qu’elle soit différente de x (sinon (∀ x,A)[x← v]=(∀ x,A) et la propriété est trivialement vraie.
On doit montrer (∀ z,A)[x← t]⇒ (∀ z,A)[x← u], c’est-à-dire
(∀ z,(A[x← t]))⇒ ∀ z,(A[x← u])
Par hypothèse de récurrence on sait que (A[x← t])⇒ (A[x← u])
quelle que soit la valeur que l’on donne pour z dans l’environnement.
On en déduit que (∀ z,(A[x← t]))⇒ (A[x← u]) est vraie pour toute valeur possible de z. En effet si on prend une valeur pour z et que ∀ z,(A[x← t]) est vrai alors A[x← t] est a fortiori vrai pour cette valeur de z et donc A[x← u].
De (∀ z,(A[x← t]))⇒ (A[x← u]) vrai pour toutes les valeurs de z, on déduit que (∀ z,(A[x← t]))⇒ ∀ z,(A[x← u]) est vrai.
On procède de manière analogue pour le quantificateur existentiel.
Si (A[x← t])⇒ (A[x← u]) est vrai
pour toute valeur de z alors (∃ z,(A[x← t]))⇒ ∃ z,(A[x← u]) est vrai. En effet si ∃ z,(A[x← t]) est vrai alors il existe une valeur v0 telle que A[x← t] est vraie pour cette valeur de z, donc A[x← u] est vraie pour cette même valeur de z (hypothèse de récurrence) et donc ∃ z,A[x← u] est vraie.
A.2 Exercices du chapitre 2
Exercice 1
Dans chacune des interprétations (qui fixent le domaine et sur ce domaine le sens des symboles ≤, < et ×), chaque formule a une valeur de vérité V ou F qu’il convient de justifier.
-
∀ x, ∃ y, x < y
-
Cette formule est vraie dans les trois interprétations ℕ, ℤ et ℚ. En effet si on se donne n’importe quelle valeur n pour x, il suffit de choisir la valeur n+1 pour y. Le résultat découle du fait que n<n+1 dans les trois interprétations.
- ∀ x, ∃ y, y < x
-
Cette formule est fausse dans l’interprétation ℕ. En effet si on choisit la valeur 0 pour x, quelle que soit n∈ℕ pour y, la propriété n<0 est toujours fausse.
- Cette formule est vraie dans les deux interprétations ℤ et ℚ. En effet si on se donne n’importe quelle valeur n pour x, il suffit de choisir la valeur n−1 pour y. Le résultat découle du fait que n−1<n dans les deux interprétations.
- ∀ x y, x < y ⇒ x+1 ≤ y
-
Cette formule est vraie dans les deux interprétations ℕ et ℤ. En effet si on se donne n’importe quelles valeurs n et m pour x et y, si x<y est vrai alors n<m et donc 0<m−n∈ℕ. Un entier strictement positif est supérieur ou égal à 1, donc 1≤ <m−n donc n+1≤ m. Ceci établit donc le résultat.
- Cette formule est fausse dans l’interprétation ℚ. En effet si on choisit la valeur 0 pour x,et la valeur 0,5 pour y, on a bien x<y qui est vrai car 0<0,5 mais x+1≤ y est faux car correspond 1≤ 0.5.
- ∀ x y z, x ≤ y ⇒ x× z ≤ y × z
-
Cette formule est vraie dans l’interprétation ℕ. En effet si on se donne n’importe quelles valeurs n et m et p dans ℕ pour x, y et z, si x≤ y est vrai dans cet environnement alors n≤ m, comme p ∈ℕ (donc positif), on a n× p≤ m× p et donc x× z ≤ y × z est vrai ce qui établit le résultat.
- Cette formule est fausse dans les interprétations ℤ et ℚ. En effet si on choisit la valeur 0 pour x, la valeur 1 pour y et la valeur −1 pour z. On a bien x≤ y est vrai car 0≤ 1. Mais x× z ≤ y × z est faux car correspond à 0≤ −1.
Exercice 2
-
La formule (∃ x,¬ P(x)) ⇒ ¬ ∀ x,P(x) est valide. On peut justifier cela avec les lois de de Morgan, car ¬ ∀ x,P(x) ≡ ∃ x,¬ P(x) et donc la formule est un cas particulier de A⇒ A qui est une tautologie. On peut aussi montrer le résultat en revenant à la définition des interprétations.
Si on se donne une interprétation I sur un domaine D telle que ∃ x,¬ P(x) est vrai dans cette interprétation alors il existe d∈ D, tel que ¬ P(x) est vrai dans cette interprétation et dans l’environnement dans lequel la variable x a la valeur d. On a donc P(x) faux dans l’interprétation I et le même environnement. On en déduit que ∀ x, P(x) faux dans l’interprétation I et donc ¬ ∀ x, P(x) est vrai.
Si on part de la formule ∃ x,¬ P(x) ⇒ ¬ ∀ x,P(x) qui se parenthèse comme ∃ x,(¬ P(x) ⇒ ¬ ∀ x,P(x)), le résultat est le même. Cette formule est valide. On peut le montrer en utilisant le fait que ∃ x,(¬ P(x) ⇒ ¬ ∀ x,P(x)) ≡ (∀ x,¬ P(x)) ⇒ ¬ ∀ x,P(x) et que si ∀ x,¬ P(x) est vrai alors a fortiori ∃ x,¬ P(x) est vrai puis se ramener au cas précédent. On peut aussi faire un raisonnement direct avec une interprétation I sur un domaine D. On choisit n’importe quel d∈ D (possible car D≠∅). On doit montrer que ¬ P(x)⇒ ¬ ∀ x,P(x) est vraie dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d. On conclut de la même manière que précédemment.
- La formule (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x) est satisfiable. Il suffit de prendre une interprétation sur un domaine D formé d’un seul élément a et telle que l’interprétation de Q est l’ensemble vide. On a donc que Q(x) est faux dans l’environnement dans lequel la variable x a la valeur a, donc ¬ Q(x) est vraie et donc aussi ∃ x,¬ Q(x) et finalement (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x).
La formule (∃ x,¬ P(x)) ⇒ ∃ x,¬ Q(x) est non valide. Il faut pour cela trouver une interprétation qui rend fausse la formule, donc qui rend vraie ∃ x,¬ P(x) et fausse ∃ x,¬ Q(x). On peut à nouveau prendre une interprétation sur un domaine D formé d’un seul élément a et telle que l’interprétation de P est l’ensemble vide et l’interprétation de Q est l’ensemble D tout entier.
Le résultat est le même avec le parenthésage ∃ x,(¬ P(x) ⇒ ∃ x,¬ Q(x)), la formule est satisfiable mais non valide.
- La formule (∃ x,¬ P(x)) ∧ ∀ x,P(x) est insatisfiable. Il faut montrer qu’elle est fausse dans toutes les interprétations. Pour cela on se donne une interprétation I sur un domaine D quelconque. Si la formule était vraie dans cette interprétation, on aurait ∃ x,¬ P(x) et donc on aurait que ¬ P(x) est vrai dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d. On aurait donc que P(x) est faux dans l’interprétation I et dans l’environnement dans lequel la variable x a la valeur d ce qui contredit le fait que ∀ x,P(x) est vrai.
On peut aussi utiliser les lois de de Morgan ¬ ∀ x,P(x)≡ ∃ x, ¬ P(x) ce qui montre que la formule est équivalente à (¬ ∀ x,P(x)) ∧ (∀ x,P(x)) qui est une instance de la formule propositionnelle ¬ A ∧ A qui est insatisfiable.
Le résultat est le même avec le parenthésage ∃ x,(¬ P(x) ∧ ∀ x,P(x)), on peut alors commencer par appliquer l’equivalence ∃ x,(¬ P(x) ∧ ∀ x,P(x)) ≡ (∃ x,¬ P(x)) ∧ (∀ x,P(x)) car ∀ x,P(x) ne dépend pas de x, ce qui nous ramène au cas précédent.
Exercice 3
On a ⊥⇒ P≡⊤, ⊤⇒ P≡ P, P⇒ ⊤≡⊤. On peut justifier par des tables de vérité ou bien utiliser A⇒ B≡ ¬ A∨ B et utiliser les lois connues pour les connecteurs ⊥, ⊤ et ∨.
Exercice 4
On suppose que x∉Vl(A).
- ∀ x,(A ⇒ H(x)) ≡ ∀ x,(¬ A ∨ H(x))≡ ¬ A ∨ ∀ x,H(x)≡
A ⇒ ∀ x, H(x)
- ∃ x,(A ⇒ H(x)) ≡∃ x,(¬ A ∨ H(x))≡ ¬ A ∨ ∃ x,H(x)≡
A ⇒ ∃ x, H(x)
- ∀ x,(G(x) ⇒ A) ≡ ∀ x,(¬ G(x) ∨ A)≡ (∀ x,¬ G(x)) ∨ A
≡¬ (∃ x, G(x)) ∨ A
≡ (∃ x, G(x)) ⇒ A
- ∃ x,(G(x) ⇒ A) ∃ x,(¬ G(x) ∨ A)≡ (∃ x,¬ G(x)) ∨ A
≡¬ (∀ x, G(x)) ∨ A≡ (∀ x, G(x)) ⇒ A
Exercice 5
Trouver des interprétations qui justifient les résultats suivants :
-
∀ x, ∃ y,R(x,y) ≢∃ y,∀ x, R(x,y)
On a ∃ y,∀ x, R(x,y)⊨ ∀ x, ∃ y,R(x,y) mais le sens inverse est faux
∀ x, ∃ y,R(x,y) ⊭∃ y,∀ x, R(x,y).
Pour montrer ce résultat, il suffit de trouver une interprétation dans laquelle ∃ y,∀ x, R(x,y) est vraie et ∀ x, ∃ y,R(x,y) est fausse.
Il suffit de prendre une interprétation avec un domaine qui contient deux éléments 0 et 1 avec pour la relation R la relation d’égalité. On a x=x et 0≠1
- ∀ x, (G(x)∨ H(x)) ≢(∀ x,G(x)) ∨ (∀ x,H(x))
On a (∀ x,G(x)) ∨ (∀ x,H(x))⊨ ∀ x, (G(x)∨ H(x)) mais le sens inverse est faux ∀ x, (G(x)∨ H(x)) ⊭(∀ x,G(x)) ∨ (∀ x,H(x))
Pour montrer ce résultat, il suffit de trouver une interprétation dans laquelle ∀ x, (G(x)∨ H(x)) est vraie et (∀ x,G(x)) ∨ (∀ x,H(x)) est fausse.
Il suffit de prendre une interprétation avec un domaine qui contient deux éléments 0 et 1 et dans laquelle G est vraie pour 0 et faux pour 1 et H est faux pour 0 et vraie pour 1. Dans cette interprétation on a bien ∀ x, (G(x)∨ H(x)) est vrai mais ∀ x,G(x) et ∀ x,H(x) sont faux.
- ∃ x, (G(x)∧ H(x)) ≢(∃ x,G(x)) ∧ (∃ x,H(x))
On a ∃ x, (G(x)∧ H(x)) ⊨ (∃ x,G(x)) ∧ (∃ x,H(x)) mais le sens inverse est faux (∃ x,G(x)) ∧ (∃ x,H(x)) ⊭∃ x, (G(x)∧ H(x))
On prend la même interprétation que dans le cas précédent. On a bien ∃ x,G(x) est vrai (prendre x↦ 0 et ∃ x,H(x) est vrai (prendre x↦ 1) et donc leur conjonction est vraie. Par contre ∃ x, (G(x)∧ H(x)) est faux car aucun des éléments du domaine ne rend vraie la formule.
Exercice 6
Le langage contient n constantes {c1;…;cn}. On note I,ρ⊨ A lorsque la formule A est vraie dans l’interprétation I et l’environnement ρ, c’est-à-dire lorsque valI(ρ, A)=V.
On s’intéresse aux interprétations dans lesquelles le symbole d’égalité est interprété par l’égalité dans le domaine. C’est-à-dire que
I,ρ⊨ t=u si et seulement si valI(ρ,t)=valI(ρ,u)
-
Le cardinal du domaine d’une interprétation qui rend vraie la formule ∀ x, x=c1∨… ∨ x=cn est inférieur ou égal à n. En effet la formule dit que tout élément du domaine est égal à l’interprétation d’une des constantes ci ce qui fait qu’il y a au plus n valeurs possibles. Par contre rien n’empêche deux constantes différentes d’être interprétées par la même valeur dans le domaine, donc on peut avoir strictement moins de n éléments.
Pour justifier le résultat plus formellement, on se donne une interprétation I sur un domaine D et on appelle C l’ensemble des interprétations des constantes {c1;…;cn}, à savoir C={valI(ci)|1≤ i≤ n}. On a C ⊆ D et |C|≤ n. On va montrer que D=C.
Soit donc d∈ D. Comme I⊨ ∀ x, x=c1∨… ∨ x=cn on a I,{x↦ d} ⊨ x=c1∨… ∨ x=cn et donc comme une disjonction est vraie lorsque l’une des parties est vraie, il existe i tel que I,{x↦ d} ⊨ x=ci et donc d=valI({x↦ d},x)=valI({x↦ d},ci) et donc d∈ C.
Les deux ensembles étant égaux ont même cardinal qui est inférieur à n.
- Montrons que (∀ x, x=c1∨… ∨ x=cn), (P(c1) ∧ … ∧ P(cn)) ⊨ ∀ x, P(x)
On se donne une interprétation I de l’égalité et telle que I⊨ ∀ x y, x=y ⇒ (P(x)⇒ P(y)), I⊨ ∀ x, x=c1∨… ∨ x=cn et I⊨ P(c1) ∧ … ∧ P(cn). Soit d∈ D.
On a I,{x↦ d} ⊨ x=c1∨… ∨ x=cn donc il exists i tel que I,{x↦ d} ⊨ x=c1, on a aussi I,{x↦ d}⊨ P(ci) on en déduit que I,{x↦ d}⊨ P(x) et donc I⊨ ∀ x,P(x).
On pourrait faire le même raisonnement pour l’existentielle. On peut aussi réutiliser le résultat précédent.
On peut remplacer P(x) par ¬ P(x) en utilisant la propriété 2 de remplacement d’un symbole de prédicat par une formule paramétrée. On a donc (∀ x, x=c1∨… ∨ x=cn), (¬ P(c1) ∧ … ∧ ¬ P(cn)) ⊨ ∀ x, ¬ P(x)
On utilise ensuite le fait que pour tout ensemble de formule E et deux formules A et B, E,A⊨ B est équivalent à E,¬ B⊨ ¬ A (on peut utiliser le fait que E,A⊨ B est équivalent à E⊨ A ⇒ B et la propriété de contraposée A ⇒ B≡¬ B⇒¬ A ).
Exercice 7
-
Il suffit d’introduire une constante c et de prendre
comme formule A la formule ∀ x, x=c
- On a (cas particulier de l’exercice précédent) ∀ x, x=c⊨ (∀ x,P(x)) ⇔ P(c) et ∀ x, x=c⊨ (∃ x,P(x)) ⇔ P(c) on en déduit que ∀ x, x=c⊨ (∀ x,P(x)) ⇔ (∃ x,P(x))
- S’il y a deux éléments a,b dans le domaine, on choisit une interprétation I telle que I,{x↦ a}⊨ P(x) et
I,{x↦ b}⊭P(x). On a bien I ⊨ ∃ x, P(x) mais I ⊭∀ x, P(x)
Exercice 8
Soit la formule ∀ x y, (P(x)∧ Q(y) ∧ (¬ P(a) ∨ ¬ Q(a))). Le langage des termes ne contient que la constante a, celui des prédicats contient les deux symboles P et Q.
-
Le domaine de Herbrand est l’ensemble des termes clos, ici réduit à la constante a.
- La base de Herbrand est l’ensemble des formules atomiques closes, ici réduite à deux formules P(a) et Q(a).
- Il y a quatre interprétations possibles suivant que P(a) et Q(a) valent vrai ou faux.
- La formule est universelle, elle est satisfiable si et seulement si l’ensemble de ses instances closes est satisfiable. Ici il y a une seule instance close P(a)∧ Q(a) ∧ (¬ P(a) ∨ ¬ Q(a)).
On peut faire une table de vérité
|
| | P(a) | Q(a) | P(a)∧ Q(a) ∧ (¬ P(a) ∨ ¬ Q(a)) |
| F | _ | F |
| V | F | F |
| V | V | F |
| |
|
La formule est fausse dans tous les modèles de Herbrand, elle est universelle et donc, d’après le théorème de Herbrand, elle est fausse dans n’importe quelle interprétation et elle est donc insatisfiable.
Exercice 9
-
La formule (∃ x,P(x))⇒∀ x,P(x) n’est pas valide (contre exemple avec un modèle à deux élements)
- La négation de cette formule, notée B est (∃ x,P(x))∧ ∃ x,¬ P(x)
- Il n’y a pas de constante dans le langage, on en ajoute une a et le domaine de Herbrand est réduit à cette constante a. La base de Herbrand contient une formule atomique P(a) et il y a donc deux interprétations possibles suivant que P(a) est vraie ou fausse.
- Il n’y a pas de modèle de Herbrand qui rend vraie la formule B.
- On ne peut pas appliquer le théorème de Herbrand car la formule n’est pas universelle. D’ailleurs la formule est satisfiable (on peut construire un modèle avec deux éléments ou dire que si elle était satisfiable alors sa négation serait valide, ce qui n’est pas le cas comme montré à la question 1).
A.3 Exercices du chapitre 3
Exercice 1
La fonction clauseset prend pour argument un ensemble
d’instances de prédicats associés à des booléens et renvoie une
formule de la logique correspondant à la clause associée.
| clauseset(s) =
| | si s=∅ alors ⊥ |
| sinon | | soit (p,b)∈ s,s′=s\ (p,b),
A=si b alors p sinon ¬
p |
| dans si s′=∅ alors A sinon A∨clauseset(s′) |
|
|
|
Exercice 2
L’argument étant déjà en forme normale de négation il n’y a pas de symbole d’implication ni de négation autre que dans un littéral.
On peut donc simplifier la fonction fnc.
|
| | fnn2fnc(⊥) | = {⊥} |
| fnn2fnc(⊤) | =∅ |
| fnn2fnc(l) | ={l} l littéral |
| fnn2fnc(P∧ Q) | =fnn2fnc(P)⋃ fnn2fnc(Q) |
| fnn2fnc(P∨ Q) | =sh(fnn2fnc(P),fnn2fnc(Q)) |
|
Exercice 3
Toute formule P peut se ramener à un ensemble de clauses E (équivalent ou équisatisfiable).
Tout modèle de la formule initiale est (ou peut s’étendre) en un modèle de chacune des clauses de E.
On va d’abord montrer que l’on peut transformer une clause C de E en un ensemble de clauses à 3 littéraux équisatisfiable.
Si une clause C a strictement plus de trois littéraux alors elle s’écrit l1∨ l2∨ D avec l1,l2 des littéraux et D une clause qui a deux littéraux de moins que C.
On introduit une nouvelle variable propositionnelle xD, on transforme la clause C en l’ensemble de clauses {l1∨ l2∨ xD,¬ xD ∨ D}. La clause l1∨ l2∨ xD a trois littéraux et la clause ¬ xD ∨ D a strictement moins de littéraux que C ce qui permet d’itérer le processus jusqu’à qu’il ne reste plus que trois littéraux. Si on a un modèle de {l1∨ l2∨ xD,¬ xD ∨ C′}. alors suivant la valeur de xD dans ce modèle on aura que l1∨ l2 ou D est vrai et donc l1∨ l2∨ D est vrai. Dans le sens inverse, s’il existe un modèle de l1∨ l2∨ D alors il suffit de choisir pour valeur de xD la valeur de la clause D dans cette interprétation pour obtenir un modèle de {l1∨ l2∨ xD,¬ xD ∨ D}.
On a ainsi traité une clause de la forme clausale de P, il faut justifier que si on met à plat tous les ensembles de clauses à trois littéraux obtenues pour toutes les clauses de E, on a toujours un ensemble de clauses equisatisfiable. Cela découle du fait qu’on introduit à chaque fois des variables nouvelles et qu’on ne modifie pas l’interprétation des symboles de la formule originale, les modèles trouvés pour chacun des ensembles de clauses à trois littéraux peuvent ainsi se recoller pour donner un modèle de l’ensemble complet de clauses.
Exercice 4
A =def (∃ x, ∀ y, R(x,y)) ⇒ (∀ y, ∃ x, R(x,y)).
-
La forme normale de négation de la formule ¬ A est
(∃ x, ∀ y, R(x,y))∧ (∃ y, ∀ x, ¬ R(x,y))
- La forme de skolem de la formule ¬ A introduit deux constantes a et b
(∀ y, R(a,y))∧ ∀ x, ¬ R(x,b)
- La forme clausale de ¬ A a deux clauses {R(a,y);¬ R(x,b)}
- L’ensemble des instances closes dans le modèle de Herbrand contient {R(a,b);¬ R(a,b)} qui est insatisfiable.
La formule ¬ A est donc insatisfiable et la formule A est valide.
Exercice 5
-
On introduit tout d’abord la fonction form qui étant donné un arbre de décision binaire (BDT) calcule une formule en forme normale de négation qui représente la même fonction booléenne.
| | | form(V)=⊤ form(F)=⊥ |
| form(IF(x,P,Q))=(x ∧ form(P)) ∨ (¬ x ∧ form(Q)) |
|
On peut alternativement utiliser la définition form(IF(x,P,Q))= (¬ x ∨ form(P)) ∧ (x ∨ form(Q)).
On transforme cette fonction en une nouvelle fonction formc qui calcule directement la forme normale conjonctive sous la forme d’un ensemble de clauses.
| | | formc(V)=∅ formc(F)={⊥} |
| formc(IF(x,P,Q))={¬ x ∨ C|C∈ formc(P)}⋃ {x ∨ C|C∈ formc(Q)} |
|
- La fonction notd se définit simplement par un parcours de l’arbre qui se contente de remplacer les feuilles par leur négation.
| | | notd(V)=F notd(F)=V |
| notd(IF(x,P,Q))=IF(x,notd(P),notd(Q))
|
|
On vérifie simplement par récurrence sur la structure de l’arbre qu’on a bien le bon comportement à savoir que pour un arbre t et une interprétation I quelconque, on a I⊨ notd(t) si et seulement si I⊭t. C’est évident pour les feuilles. Dans le cas d’une construction IF(x,P,Q), il suffit de distinguer les cas où I(x)=V et I(x)=F et de conclure par hypothèse de récurrence.
- Pour implanter la conjonction de deux BDT, la principale difficulté est que les deux arbres ne sont pas forcément construits sur la même séquence de variables. La fonction doit donc réconcilier deux branches en intercalant possiblement des variables qui seraient présentes sur une seule des branches et en préservant la contrainte de variables ordonnées de manière croissante sur chaque branche.
| | | conjd(b1,b2)=b1 et b2 |
| conjd(IF(x,P1,Q1),IF(y,P2,Q2))=IF(x,conjd(P1,P2),conjd(Q1,Q2)) si x=y |
| conjd(IF(x,P,Q),R)=IF(x,conjd(P,R),conjd(Q,R))
si vars de R plus grandes que x |
| conjd(R,IF(y,P,Q))=IF(y,conjd(R,P),conjd(R,Q))
si vars de R plus grandes que y |
|
Les deux derniers cas couvrent également la situation dans laquelle R est une feuille (pas de variable).
La terminaison de cette définition est justifiée par le fait que le nombre de symboles IF est strictement plus petit dans les arguments des appels à la fonction conjd à droite.
- Le BDT d’une formule valide n’a que des feuilles V, celui d’une formule insatisfiable n’a que des feuilles F et une formule satisfiable aura au moins une feuille V.
- Pour trouver un modèle, on parcourt l’arbre pour chercher une feuille avec la valeur V. On renvoie insat si la formule est insatisfiable et sinon une interprétation (sous forme de liste de couples variable/valeur).
| | | mod(V)=[] mod(F)=insat |
| mod(IF(x,P,Q))=(x,V)::mod(P) si mod(P)≠insat |
| mod(IF(x,P,Q))=(x,F)::mod(Q) si mod(P)=insat et mod(Q)≠insat |
| mod(IF(x,P,Q))=insat si mod(P)=insat et mod(Q)=insat |
|
Exercice 6
-
L’ordre sur les variables est x < y < z < t. Les OBDDs des formules (z ⇔ t) et (x ⇔ y) ∧ (z ⇔ t) sont
[level distance=10mm,
every node/.style=circle,draw,solid,inner sep=2pt
]
at (0,0)
z
child node (tnodel)
t
child node[rectangle,draw] (V)
V
child[dashed] node (tnoder)
t
child[solid] node[rectangle,draw] (F)
F
;
[dashed] (tnoder) – (V);
[dashed] (tnodel) – (F);
at (5,0) (xnode) x
child node (ynodel) y
child node (znode) z
child node (tnodel) t
child node[rectangle,draw] (V) V
child[dashed] node (tnoder) t
child[solid] node[rectangle,draw] (F) F
child[dashed] node (ynoder) y
;
[dashed] (tnoder) – (V);
[dashed] (tnodel) – (F);
[solid] (ynoder) .. controls +(0,-1) and +(.5,.5) .. (F.north east);
[dashed] (ynoder) – (znode);
[dashed] (ynodel) .. controls +(1,0) and +(.5,1) .. (F.north east);
- On associe à chaque sommet du graphe une formule équivalente au sous-graphe issu de ce sommet qui n’utilise que des littéraux et les symboles ∨ et ∧.
[level distance=10mm,
every node/.style=circle,draw,solid,inner sep=2pt
]
at (0,0)
z
child node (tnodel)
t1
child node[rectangle,draw] (V)
V
child[dashed] node (tnoder)
t2
child[solid] node[rectangle,draw] (F)
F
;
[dashed] (tnoder) – (V);
[dashed] (tnodel) – (F);
at (5,0) (xnode) x
child node (ynodel) y1
child node (znode) z
child node (tnodel) t
child node[rectangle,draw] (V) V
child[dashed] node (tnoder) t
child[solid] node[rectangle,draw] (F) F
child[dashed] node (ynoder) y2
;
[dashed] (tnoder) – (V);
[dashed] (tnodel) – (F);
[solid] (ynoder) .. controls +(0,-1) and +(.5,.5) .. (F.north east);
[dashed] (ynoder) – (znode);
[dashed] (ynodel) .. controls +(1,0) and +(.5,1) .. (F.north east);
-
La formule associée à la feuille V est ⊤ et à la feuille F est ⊥
- si un nœud est étiqueté par la variable x dont le fils vrai correspond à la formule A et le fils faux à la formule B alors la formule ssociée au nœud x est x∧ A∨ ¬ x∧ B qui peut parfois se simplifier
| t1 | : | t |
| t2 | : | ¬ t |
| z | : | (z ∧ t) ∨ (¬ z ∧ ¬ t) |
| y1 | : | y ∧ ((z ∧ t) ∨ (¬ z ∧ ¬ t)) |
| y2 | : | ¬ y ∧ ((z ∧ t) ∨ (¬ z ∧ ¬ t)) |
| x | : | ( x ∧ y ∧ ((z ∧ t) ∨ (¬ z ∧ ¬ t)))
∨ (¬ x ∧ ¬ y ∧ ((z ∧ t) ∨ (¬ z ∧ ¬ t)))
|
|
- Deux formules sont équivalentes si et seulement si elles sont représentées par le même OBDD.
Si deux formules ont le même OBDD, elles ont a fortiori la même table de vérité et sont donc équivalentes.
Dans l’autre sens, on montre que deux OBDD t et u différents ne sont pas associés à des formules équivalentes, on raisonne par récurrence sur le nombre de variables propositionnelles qui apparaissent dans les OBDD.
S’il n’y a pas de variable alors on a deux valeurs booléennes qui sont différentes et donc les formules initiales ne sont pas équivalentes.
Si l’un des OBDD n’est pas une valeur booléenne, on considère x la plus petite variable, on peut supposer que c’est t qui débute par la variable x.
Si x n’apparait pas dans u alors cela veut dire que la formule Q associée à u ne dépend pas de x. Par contre les deux OBDD fils n et m de x dans t sont différents. Par hypothèse de récurrence (moins de variables) ils ne sont pas équivalents donc il existe une interprétation I qui rend vraie l’une et fausse l’autre. On regarde la valeur de u dans cette interprétation, elle est différente soit de l’interprétation de n, soit de l’interprétation de m et il suffit de fixer x à la valeur correspondante pour trouver une interprétation dans laquelle les deux formules diffèrent.
Dans le cas où x apparait dans u alors il est forcément en tête (plus petite variable) et si les OBDD t et u sont différents cela signifie qu’ils n’ont pas le même fils vrai ou pas le même fils faux. Dans les deux cas par récurrence on trouve une interprétation qui ne donne pas la même valeur et on l’étend avec la bonne valeur de x.
On peut ainsi simplement caractériser la validité et satisfiabilité d’une formule
-
une formule valide a un OBDD qui est réduit à une feuille V,
- une formule insatisfiable a un OBDD qui est réduit à une feuille
F.
- tout OBDD qui n’est pas juste une feuille F correspond à une
formule satisfiable
- un modèle de la formule est donné par n’importe quelle branche qui mène jusqu’à
une feuille V.
-
partage maximal (nœud et feuilles), il n’y a pas deux sommets différents qui ont les même caractéristiques :
pour tous sommets n et m,
-
si noeud(G,n) et noeud(G,m)
et var(G,n)=var(G,m) et vrai(G,n)= vrai(G,m) et faux(G,n)= faux(G,m) alors n=m
- si feuille(G,n) et feuille(G,m) et valeur(G,n)= valeur(G,m) alors n=m
- absence de tests inutiles: pour tout sommet n,
si noeud(G,n) alors vrai(G,n)≠faux(G,n)
- ordre sur les variables : pour tout sommet n,
si noeud(G,n) et noeud(G,vrai(G,n)) alors var(G,n) < var(G,vrai(G,n))
si noeud(G,n) et noeud(G,faux(G,n)) alors var(G,n) < var(G,faux(G,n))
- La fonction naive a la forme suivante
form(G,n) =
si feuille(G,n) alors si valeur(G,n) alors ⊤ sinon ⊥
sinon soit x = var(G,n)
soit P = form(vrai(G,n))
soit Q = form(faux(G,n))
(¬ x ∨ P) ∧ (x ∨ Q)
Pour justifier de la terminaison on remarque que la plus petite variable présente dans le graphe traité augmente strictement dans le cas d’un appel et donc qu’on aboutit toujours à une feuille.Pour exploiter le partage, il faut utiliser des techniques de programmation dynamique en stockant dans une table les résultats déjà calculés pour chaque sommet. Si la valeur a déjà été calculée, on la renvoie sionon on la calcule comme précédemment et on l’enregistre avant de renvoyer la valeur.
- G est le graphe courant, x une variable propositionnelle, n et m sont deux sommets de G. On veut calculer un nouveau graphe G′ et un noeud p tel que form(G′,p)≡IF(x,form(G,n), form(G,m)) et form(G′,k)=form(G,k) pour tous les sommets de G. On utilise une table T(G) qui permet de retrouver si une formule est déjà représentée dans le graphe : soit une variable y et deux sommets n et m, (x,n,m)↦ p ∈ T(G) ssi le graphe G a un sommet p étiqueté par la variable x dont le fils “vrai” est le sommet n et le fils “faux” est le sommet m.
if(G,x,n,m) =
si (x,n,m) ↦ p dans T alors (G,p)
sinon si n=m alors (G, n)
sinon soit p = nouveau sommet
soit G’ = G + p / var(p)=x, vrai(p)=n, faux(p)=m
ajouter (x,n,m)↦ p dans T
(G’,p)
- On veut compter le nombre de modèles d’une formule représentée par un OBDD.
-
Soit l’OBDD suivant sur les variables propositionnelles x1,x2,x3,x4,x5 :
[level distance=8mm,
every node/.style=circle,draw,solid,inner sep=2pt
]
x1
child [level distance=10mm] node (x3) x3
child [level distance=9mm] node (x4) x4
child [level distance=9mm] node[rectangle,draw] (V) V
child [level distance=10mm]node (x2) x2 edge from parent [dashed]
child [level distance=9mm]node (x5) x5 edge from parent [solid]
child[level distance=9mm]node[rectangle,draw] (F) F
;
[dashed] (x2) – (x3);
[dashed] (x3) – (x5);
[dashed] (x4) – (F);
[dashed] (x5) – (V);
on annote l’OBDD pour donner le nombre d’interprétations concernant les variables plus grandes que celle du nœud n qui satisfont la formule associée à n.
| | | x5 | : | 1 | {x5 ↦ F} |
| x4 | : | 2 | {x4↦ V; x5 ↦ F},{x4↦ V; x5 ↦ V} |
| x3 | : | 2+2 = 4 | {x3↦ V}⋃ I(x4), {x3↦ F,x4↦ V/F}⋃ I(x5) |
| x2 | : | 4 + 4 = 8 | {x2↦ F}⋃ I(x3), {x2↦ V,x3↦ V/F,x4↦ V/F}⋃ I(x5) |
| x1 | : | 8 + 8 | {x1↦ F}⋃ I(x2), {x1↦ V,x2↦ V/F}⋃ I(x3) |
|
- la fonction indice calcule pour chaque sommet de l’OBDD un entier qui est la position de la variable dans l’ordre si le sommet est un nœud, et si le sommet est une feuille, l’indice est n+1 avec n le nombre total de variables.
nbsat calcule pour un graphe G et un sommet n, le nombre de modèles de la formule en ne considérant que les variables plus grandes que celle du sommet.
nbsat(G,n) =
si feuille(G,n)
alors si valeur(G,n) alors 1 sinon 0
sinon soit p = indice(n)
soit v = vrai(G,n)
soit f = faux(G,n)
2^(indice(v)-indice(n)-1) × nbsat(G,v)
+ 2^(indice(f)-indice(n)-1) × nbsat(G,f)
- Il faut ajouter les interprétations des variables plus petites que celle qui apparait au sommmet de l’OBDD
nbsat1(G,n)= 2^(indice(n)-1) × nbsat(G,n)
Exercice 9
On utilise les règles de la déduction naturelle.
- Pour la formule A ⇒ (B ⇒ A) on se ramène par deux
introduction de ⇒ à prouver A sous les
hypothèses A,B ce qui est vrai par hypothèse.
Cette preuve s’écrit sous forme d’arbre de dérivation :
- Pour la formule (A ⇒ ¬ A) ⇒ ¬ A on se ramène par une introduction de ⇒ et une introduction de ¬ à prouver l’absurde ⊥ sous les hypothèses A ⇒ ¬ A, A. Pour cela on va utiliser l’élimination de la négation en essayant de prouver à la fois A (vrai par hypothèse) et ¬ A. Cette dernière propriété s’obtient simplement par Modus Ponens en utilisant
A ⇒ ¬ A vrai par hypothèse et A qui est aussi vrai par hypothèse.
- Pour montrer (∃ x,P(x)) ⇒ ¬ ∀ x,¬ P(x),
on effectue deux introductions (⇒ suivi de ¬). On a pour hypothèses
∃ x,P(x) et ∀ x,¬ P(x) et il faut montrer une contradiction.
Pour cela on procède par élimination de la propriété existentielle ∃ x, P(x) qui est vraie par hypothèse et on peut donc introduire un nouvel objet y et une hypothèse P(y), on doit toujours montrer une contradiction, ce que l’on fait en montrant à la fois ¬ P(y) et P(y). La première propriété s’obtient par élimination de la quantification universelle ∀ x, ¬ P(x) sur l’objet y et la seconde est juste une hypothèse. Cela donne l’arbre de dérivation suivant :
| ⇒ I | | ¬ I | | ∃ H | | | | ¬ E | |
| | ∀ E | | hyp | |
| |
| | (∀ x,¬ P(x)) , P(y) ⊢∀ x,¬ P(x) |
|
| |
| | (∃ x,P(x)), (∀ x,¬ P(x)) , P(y) ⊢ ¬ P(y) |
| | | hyp | |
| |
| | (∃ x,P(x)), ∀ x,¬ P(x) , P(y) ⊢ P(y) |
|
|
| |
| | (∃ x,P(x)),(∀ x,¬ P(x)), P(y) ⊢ ⊥ |
|
|
| |
| | (∃ x,P(x)), (∀ x,¬ P(x)) ⊢ ⊥ |
|
| |
| | ∃ x,P(x) ⊢ ¬ ∀ x,¬ P(x) |
|
| |
| | ⊢ (∃ x,P(x)) ⇒ ¬ ∀ x,¬ P(x) |
|
|
| | ∀ I | | ¬ I | | ¬ H | | ∃ I | | hyp | |
| |
| | ¬ ∃ x,P(x),P(y) ⊢ P(y) |
|
| |
| | (¬ ∃ x,P(x)),P(y) ⊢ ∃ x,P(x) |
|
| |
| | (¬ ∃ x,P(x)),P(y) ⊢ ⊥ |
|
| |
| | (¬ ∃ x, P(x)) ⊢ ¬ P(y) |
|
| |
| | ¬ ∃ x, P(x) ⊢ ∀ y, ¬ P(y) |
|
Exercice 10
On utilise les règles de la déduction naturelle en particulier la règle de raisonnement par l’absurde.
-
| abs | | ¬ E | | ∨ Ig | | ¬ I | | ¬ E | | ∨ Id | |
| |
| | ¬(¬ P ∨ P), P ⊢ ¬ P ∨ P |
|
| |
| | ¬(¬ P ∨ P), P ⊢ ⊥ |
|
| |
| | ¬(¬ P ∨ P)⊢ ¬ P |
|
| |
| | ¬ (¬ P ∨ P) ⊢ ¬ P ∨ P |
|
| |
| | ¬ (¬ P ∨ P) ⊢ ⊥ |
|
| |
| | ⊢ ¬ P ∨ P |
|
|
| | ∃ I | |
| | ⇒ I | | hyp | |
| |
| | (∀ x, ¬ P(x)),¬ P(a) ⊢ ∀ y,¬ P(y) |
|
| |
| | (∀ x, ¬ P(x)) ⊢ ¬ P(a) ⇒ ∀ y,¬ P(y) |
|
|
| |
| | (∀ x, ¬ P(x)) ⊢ ∃ x, (¬ P(x) ⇒ ∀ y,¬ P(y)) |
|
s’il existe quelqu’un qui boit alors c’est lui qu’on choisit et d’affirmer qu’il est non buveur introduit une contradiction et nous permet de déduire que personne ne boit …|
| | ∃ E | | ∃ I | | ⇒ I | | ¬ E | |
| |
| | P(x), ¬ P(x) ⊢ ∀ y,¬ P(y) |
|
| |
| | P(x) ⊢ ¬ P(x) ⇒ ∀ y,¬ P(y) |
|
| |
| | P(x) ⊢ ∃ x, (¬ P(x) ⇒ ∀ y,¬ P(y)) |
|
| |
| | (∃ x, P(x)) ⊢ ∃ x, (¬ P(x) ⇒ ∀ y,¬ P(y)) |
|
On raisonne par cas si ∃ x, P ou ¬ (∃ x, P)|
| | cut | | ⊢ (∃ x,P) ∨ ¬ (∃ x, P)
| | ∨ E | | (∃ x,P) ⊢ B
| | cut | ¬ (∃ x,P) ⊢ ∀ x, ¬ P
¬ (∃ x,P), (∀ x, ¬ P) ⊢ B
|
| |
| | ¬ (∃ x,P) ⊢ B |
|
|
| |
| | (∃ x,P) ∨ ¬ (∃ x, P) ⊢ B |
|
|
| |
| | ⊢ B |
|
Exercice 11
On utilise les règles du calcul des séquents à conclusions multiples.
-
-
| ¬ g | | ∀ d | | ¬ d | | | | ∃ d | | hyp | |
| |
| | P(y), ⊢ P(y), (∃ x,P(x)) |
|
| |
| | P(y)⊢ (∃ x,P(x)) |
|
|
| |
| | ⊢ (∃ x,P(x)), ¬ P(y) |
|
| |
| | ⊢ (∃ x,P(x)), (∀ x,¬ P(x)) |
|
| |
| | ¬ ∀ x,¬ P(x)⊢ ∃ x,P(x) |
|
- La négation se traite simplement en faisant changer de côté la formule.
- pour traiter le lemme du buveur il est nécessaire de commencer par introduire un objet arbitraire a afin de pouvoir
décomposer ensuite le reste de la formule qui nous donnera l’élément pour conclure la preuve.
| ∃ d | | ⇒ d | | ∀ d | | | | ¬ d | | | | ∃ d | | ⇒ d | | ¬ g | | hyp | |
| |
| | ¬ P(a),P(z) ⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), (∀ y, ¬ P(y)),P(z) |
|
| |
| | ¬ P(a),P(z),¬ P(z) ⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), (∀ y, ¬ P(y)) |
|
| |
| | ¬ P(a),P(z)⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), (¬ P(z) ⇒ ∀ y, ¬ P(y)) |
|
| |
| | ¬ P(a),P(z)⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)) |
|
|
| |
| | ¬ P(a)⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), ¬ P(z) |
|
|
| |
| | ¬ P(a)⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), (∀ y, ¬ P(y)) |
|
| |
| | ⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)), (¬ P(a) ⇒ ∀ y, ¬ P(y)) |
|
| |
| | ⊢ ∃ x, (¬ P(x) ⇒ ∀ y, ¬ P(y)) |
|
A.4 Exercices du chapitre 4
Exercice 1
-
Montrons que l’interprétation de Herbrand dans laquelle P(u,v) est vrai si et seulement si u∼ v est un modèle des formules A0, A1, A2, A3.
Il faut montrer :
-
e∼ e (vrai avec la séquence vide),
- Soit u et v deux termes quelconques, si u∼ v alors
a(u),b(a(a(v)) qui est vrai en ajoutant 1 en tête de la séquence qui fait
correspondre u et v et de même pour les deux autres propriétés en utilisant le 2ème et le 3ème couple.
- On montre que si u∼ v alors
A0,A1,A2,A3⊨ P(u,v) par
récurrence sur la taille de la séquence i1,…,ik.
-
Si la séquence est vide alors les termes u et v
correspondent au mot vide donc au terme e. Il faut montrer
A0,A1,A2,A3⊨ P(e,e) ce qui est vrai (A0).
- On suppose la propriété vraie pour toutes les séquences de
taille k et on veut montrer que c’est vrai pour une sequence
de taille k+1. On a donc une séquence i0,i1,…,ik et
un terme u qui correspond au mot ui0ui1…
uik et le terme v correspond au mot vi0vi1…
vik. On introduit aussi le terme u′ qui correspond au mot
ui1… uik et le terme v correspond au mot
vi1… vik Par hypothèse de récurrence on a
A0,A1,A2,A3⊨ P(u′,v′) et en utilisant la propriété
Ai0 on en déduit A0,A1,A2,A3⊨ P(u,v). On
pourra détailler le cas i0=1 et admettre que les autres cas
sont pareils.
- On a A0 ⊨ ∃ x,P(x,x), trivialement en prenant le terme e pour x.
- Une solution du problème de Post nous donne une séquence et un
mot non vide u tel que A0,A1,A2,A3⊨ P(u,u). Comme
ce mot est non vide, il s’écrit de la forme a(u′) ou b(u′) donc on a bien
A0,A1,A2,A3⊨
∃ x,(P(a(x),a(x))∨ P(b(x),b(x))).
- Il suffit de se placer dans le modèle dans lequel P(u,v) est vrai si et seulement si u∼ v. Le modèle valide A0,A1,A2,A3 et donc valide ∃ x,(P(a(x),a(x))∨ P(b(x),b(x))) d’où l’existence d’un terme u tel que
a(u)∼ a(u) est vrai ou bien b(u) ∼ b(u). Dans les deux cas on a une solution au problème de Post.
Exercice 2
- L’arbre de dérivation pour le séquent ⊢ ((p∧ q) ⇒ r) ⇒ (¬ p ∨ q) ⇒ (p ⇒ r) est :
|
| | ⇒ d | |
| | ⇒ d | |
| | ⇒ d | |
| | ⇒ g | | ∧ d | |
| |
| | (¬ p ∨ q), p ⊢ r,p∧ q |
|
| |
|
| |
| | ((p∧ q) ⇒ r), (¬ p ∨ q), p ⊢ r |
|
|
| |
| | ((p∧ q) ⇒ r), (¬ p ∨ q) ⊢ (p ⇒ r) |
|
|
| |
| | ((p∧ q) ⇒ r) ⊢ (¬ p ∨ q) ⇒ (p ⇒ r) |
|
|
| |
| | ⊢((p∧ q) ⇒ r) ⇒ (¬ p ∨ q) ⇒ (p ⇒ r) |
|
Les feuilles de l’arbre correspondent à des règles hypothèses donc la formule est valide.
- L’arbre de dérivation pour le séquent ⊢ ((p∧ q) ⇒ r) ∧ (¬ p ∨ q) ⇒ p est
|
| | ⇒ d | | ∧ g | | ⇒ g | |
| |
| | ((p∧ q) ⇒ r),(¬ p ∨ q) ⊢ p |
|
| |
| | ((p∧ q) ⇒ r) ∧ (¬ p ∨ q) ⊢ p |
|
| |
| | ⊢ ((p∧ q) ⇒ r) ∧ (¬ p ∨ q) ⇒ p |
|
On observe sur cet arbre qu’il y a au moins une feuille qui n’est pas une hypothèse, par exemple ⊢ p qui n’est pas vrai dans l’interprétation où p est faux. Donc la formule n’est pas valide.
Exercice 3
L’ensemble {p∨ q,¬ p∨¬ q,p∨ ¬ q, ¬ p∨ q} est insatisfiable :
On a utilisé deux fois la dérivation de la clause p.
Exercice 4
-
-
(¬ p ∨ ¬ q ∨ ¬ r) ∧ (¬ p ∨ q ∨ r)
∧ (p ∨ q ∨ ¬ r)
| Unsat | |
| | Bcp | |
| | Unsat | ⋮ ⋮ |
| |
| | {r↦ V}≫¬ p ∨ ¬ q, p ∨ q |
|
|
| |
| |
{r↦ V}≫¬ p ∨ ¬ q ∨ ¬ r, ¬ p ∨ q ∨ r, p ∨ q ∨ ¬
r
|
|
| | Bcp | |
| | Unsat | |
| | Bcp | |
| | Assume | |
| | success | |
| |
| | {r↦ F;p↦ V;q↦ V}≫∅ |
|
|
| |
| | {r↦ F;p↦ V}≫ q
|
|
|
| |
| | {r↦ F;p↦ V}≫¬ p ∨ q
|
|
| |
|
| |
| | {r↦ F}≫¬ p ∨ q
|
|
|
| |
| |
{r↦ F}≫¬ p ∨ ¬ q ∨ ¬ r, ¬ p ∨ q ∨ r, p ∨ q ∨ ¬ r
|
|
|
| |
| |
{}≫¬ p ∨ ¬ q ∨ ¬ r, ¬ p ∨ q ∨ r, p ∨ q ∨ ¬ r
|
|
On trouve plusieurs modèles : {r↦ F;p↦ V;q↦ V}, {r↦ F;p↦ F;q↦ V/F}
- (p∨ r) ∧ (¬ q ∨ p) ∧ ¬ p ∧ ¬ r
| Assume | | Bcp | |
| | Assume | |
| | Bcp | | Conflict | |
| |
| | {r↦ F;p↦ V}≫ ¬ q,⊥ |
|
| |
| | {r↦ F;p↦ V}≫ ¬ q,¬ p |
|
|
| |
| | {r↦ F}≫ p,¬ q,¬ p
|
|
|
| |
| | {r↦ F}≫ p∨ r,¬ q ∨ p,¬ p
|
|
| |
| | {}≫ p∨ r,¬ q ∨ p,¬ p,¬ r |
|
La formule est insatisfiable.
- La construction de l’arbre par les règles DPLL est toujours finie
Les règles Bcp et Assume font diminuer le nombre de littéraux dans la partie droite Δ du jugement I≫ Δ. La règle Unsat ne modifie pas Δ mais ajoute une variable dans l’interprétation. Comme le nombre de variables que l’on peut affecter est fini (c’est le nombre de variables qui apparaissent dans les clauses de Δ), soit N se nombre, la quantité N−n avec n le nombre de variables affectées dans I diminue strictement. On a donc deux quantités: le nombre de littéraux dans Δ et le nombre de variables de Δ non affectées dans I dont la somme décroit strictement le long d’une branche de l’arbre. Les branches sont donc finies.
- On montre que les règles de DPLL sont correctes. C’est-à-dire que si un arbre DPLL de racine I≫ Δ contient une feuille de succès J ≫ ∅ alors l’interprétation J étend l’interprétation I (c’est-à-dire que I(x)=J(x) pour toutes les variables x qui apparaissent dans I) et l’interprétation J rend vraies toutes les clauses de Δ.
On raisonne par minimalité sur l’arbre de dérivation DPLL.
-
Si on a une feuille, soit c’est une feuille de succès I ≫ ∅ et alors comme Δ est vide on a que I rend vrai les clauses de Δ et la seule feuille de succès dans cet arbre est la feuille elle-même.
Si c’est une feuille de conflit alors il n’y a pas de feuille de succès et donc la propriété est vraie.
- Si on a une règle BcpV alors comme on a une seule prémisse
I ≫ Δ, si l’arbre contient une feuille de succès J ≫ ∅, elle est dans ce sous-arbre et donc J étend I et rend vrai les formules de Δ.
On a J(l)=I(l)=V et donc J rend vrai aussi l∨ C.
- Si on a une règle BcpF alors comme on a une seule prémisse
I ≫ Δ,C, si l’arbre contient une feuille de succès J ≫ ∅, elle est dans ce sous-arbre et donc J étend I et rend vrai les formules de Δ,C et donc J rend vrai aussi l∨ C.
- Si on a une règle AssumeV alors comme on a une seule prémisse
I+{x↦ V} ≫ Δ, si l’arbre contient une feuille de succès J ≫ ∅, elle est dans ce sous-arbre et donc J étend I+{x↦ V} et rend vrai les formules de Δ.
On a J(x)=V et donc J rend vrai aussi Δ,x.
- Si on a une règle AssumeF alors comme on a une seule prémisse
I+{x↦ F} ≫ Δ, si l’arbre contient une feuille de succès J ≫ ∅, elle est dans ce sous-arbre et donc J étend I+{x↦ F} et rend vrai les formules de Δ.
On a J(x)=F et donc J rend vrai aussi Δ,¬ x.
- Si on a une règle Unsat alors il y a deux prémisses donc la feuille de succès J ≫ ∅ peut se trouver dans l’une des deux branches (ou dans les deux). Dans les deux cas on a que J étend I+{x↦ V/F} et donc J étend I et J rend vrai les formules de Δ.
- Pour trouver un modèle d’une formule :
-
On met la formule en forme normale conjonctive, on obtient
ainsi un ensemble de clauses Δ.
- On applique la méthode DPLL en partant du problème {}≫ Δ.
- Si on arrive à une feuille de succès I≫ ∅ alors I est un modèle (on peut choisir des valeurs arbitraires pour les variables de Δ qui ne seraient pas affectées dans I
L’arbre n’est pas unique et on peut choisir différentes stratégies pour trouver une branche de succès plus rapidement.
- Il suffit de montrer que si on a un arbre DPLL de racine I≫ Δ alors si K est un modèle de Δ qui étend I alors il existe une feuille de succès J ≫ ∅ telle que K étend J. On regarde chaque règle:
-
si on a une règle de succès, c’est trivial. Si c’est une feuille de conflit alors il n’y a pas de modèle de ⊥ et donc la propriété est vraie.
- Pour les règles Bcp, si on a un modèle
K de Δ,(l∨ C) qui étend I alors c’est aussi un modèle de Δ et donc on a bien une feuille de succès dans la règle BcpV et pour
BcpF, comme K(l)=I(l)=F alors c’est aussi un modèle de Δ,C et donc on a une feuille de succès qui convient.
- Dans le cas des règles Assume, si K est un modèle de Δ,l qui étend I
et que l n’a pas de valeur dans l alors on a forcément K(l)=V et donc K étend I+{x↦ b} et valide Δ et donc il y a bien une feuille de succès qui convient.
- Pour la règle Unsat si K est un modèle de Δ qui étend I on regarde la valeur de K(x), si K(x)=V alors K étend I+{x↦ V} et donc on trouvera la branche de succès dans le sous-arbre gauche et si K(x)=F alors on trouvera la feuille dans le sous-arbre droit correspondant à la branche I+{x↦ F}.
Si on construit tout l’arbre alors on va trouver tous les modèles en regardant toutes les feuilles de succès et en considérant toutes les extensions.
- On peut utiliser cette méthode pour prouver la validité d’une formule.
Si on a une formule A, on trouve la forme clausale correspondant à ¬ A et on construit l’arbre DPLL. Si toutes les feuilles sont des conflits alors ¬ A est insatisfiable et donc A est valide.
Exercice 5
-
N(x,є)=? N(є,y)
Solution : {x← є;z← є}
- N(N(x,y),є) =? N(є,y)
Pas de solution : on simplifie en utilisant (7) qui amène l’équation N(x,y)=?є qui échoue (règle 6) car il faudrait rendre égaux un terme qui commence par le symbole N avec un terme qui commence par le symbole є.
- N(x,є) =? x
Pas de solution : échec règle (3) après avoir appliqué la règle (5) pour retourner l’équation. Quel que soit le terme qui remplace la varible x, la partie gauche de l’équation aura toujours plus de symboles que la partie droite.
Exercice 6
Pour chaque problème, on transforme l’ensemble des équations en indiquant la règle utilisée et on construit progressivement la substitution
-
| règle | substitution | équations |
| (7) | | |
| (4) | | |
| (5) | {x← f(y)} | |
| (4) | {x← f(y)} | |
| (1) | {x← f(y)}{z← f(y)} | ∅ |
| |
| |
Il faut ensuite développer la substitution résultat, ici on a
| {x← f(y)}{z← f(y)}={x← f(y);z← f(y)} |
| règle | substitution | équations |
| (7) | | | g(g(x,f(y)),z) | | g(g(y,z),a) |
|
| (7) | | |
| (4) | | |
| (6) | {z← a} | |
| | echec | |
| |
|
Exercice 7
-
(plus(x,0)≤ x)=? (plus(0,y)≤ y)
Solution {x← 0;y← 0}
- (plus(x,0)≤ x)=? ¬ (y ≤ z)
Pas de solution car un littéral positif ne peut être égal à un littéral négatif.
- (plus(x,0)≤ x)=? (y≤ plus(y,0))
Pas de solution : le problème se décompose en
plus(x,0)=? y; x =? plus(y,0) qui se simplifie par les règles (5) puis (4), on obtient {y← plus(x,0)}(x =? plus(plus(x,0),0)) qui conduit à un échec suivant la règle (3).
Exercice 8
Il suffit de résoudre le problème :
{t1=? t2;t2=? t3 … tn−1=? tn}
On peut se ramener à une seule équation :
F(t1,t2,…,tn−1)=F(t2,t3, …,tn)
Exercice 9
-
On peut changer l’ordre des motifs, les exécuter en parallèle lorsque :
inst(pi) ∩ inst(pj) = ∅
- Tous les cas sont couverts si
inst(p1) ∪ … ∪ inst(pn) = T(F)
- Le motif pj est inutile si
inst(pj) ⊆ inst(p1) ∪ … ∪ inst(pj−1)
Exercice 10
Pour prouver (∃ x,¬ P(x)), (∀ x,(P(x) ∨
Q(x)))⊨ ∃ x, Q(x) en utilisant la résolution, on procède par étapes :
-
Mise en forme clausale des hypothèses et de la négation de la conclusion ¬∃ x, Q(x)≡∀ x,¬ Q(x)
- Résolution :
- Conclusion : on a montré que l’ensemble (∃ x,¬ P(x)), (∀ x,(P(x) ∨
Q(x))),¬ ∃ x, Q(x) était insatisfiable, ce qui est équivalent à
(∃ x,¬ P(x)), (∀ x,(P(x) ∨
Q(x)))⊨ ∃ x, Q(x)
Exercice 11
-
Si E est un ensemble de clauses tel que chaque
clause contient au moins un littéral R(t1,…,tn) alors en choisissant pour interprétation de R la relation toujours vraie, chaque clause vaut vraie et donc l’ensemble des clauses E est satisfiable.
- Si E est un ensemble de clauses, qui ne contient aucun littéral négatif ¬ R(u1,…,un), alors E est satisfiable ssi l’ensemble {C∈E|C ne contient pas de littéral R(t1,…,tn)} est satisfiable.
Si E est satisfiable alors a fortiori tout sous ensemble de E l’est.
Si {C∈E|C ne contient pas de littéral R(t1,…,tn)} est satisfiable alors comme il n’y a pas non plus de littéral ¬ R(u1,…,un) dans cette ensemble, l’interprétation qui rend vrai cet ensemble de clause ne dépend pas de l’interprétation de R, il suffit donc de l’étendre avec pour interprétation de R la relation toujours vraie pour avoir une interprétation qui rend vraie l’ensemble de clauses E.